프로그래머스 - 교점에 별 만들기 (위클리 챌린지 10주차)

1. 문제

문제 링크

설명

Ax + By + C = 0으로 표현할 수 있는 n개의 직선이 주어질 때, 이 직선의 교점 중 정수 좌표에 별을 그리려 합니다.

예를 들어, 다음과 같은 직선 5개를

• 2x - y + 4 = 0
• -2x - y + 4 = 0
• -y + 1 = 0
• 5x - 8y - 12 = 0
• 5x + 8y + 12 = 0

좌표 평면 위에 그리면 아래 그림과 같습니다.

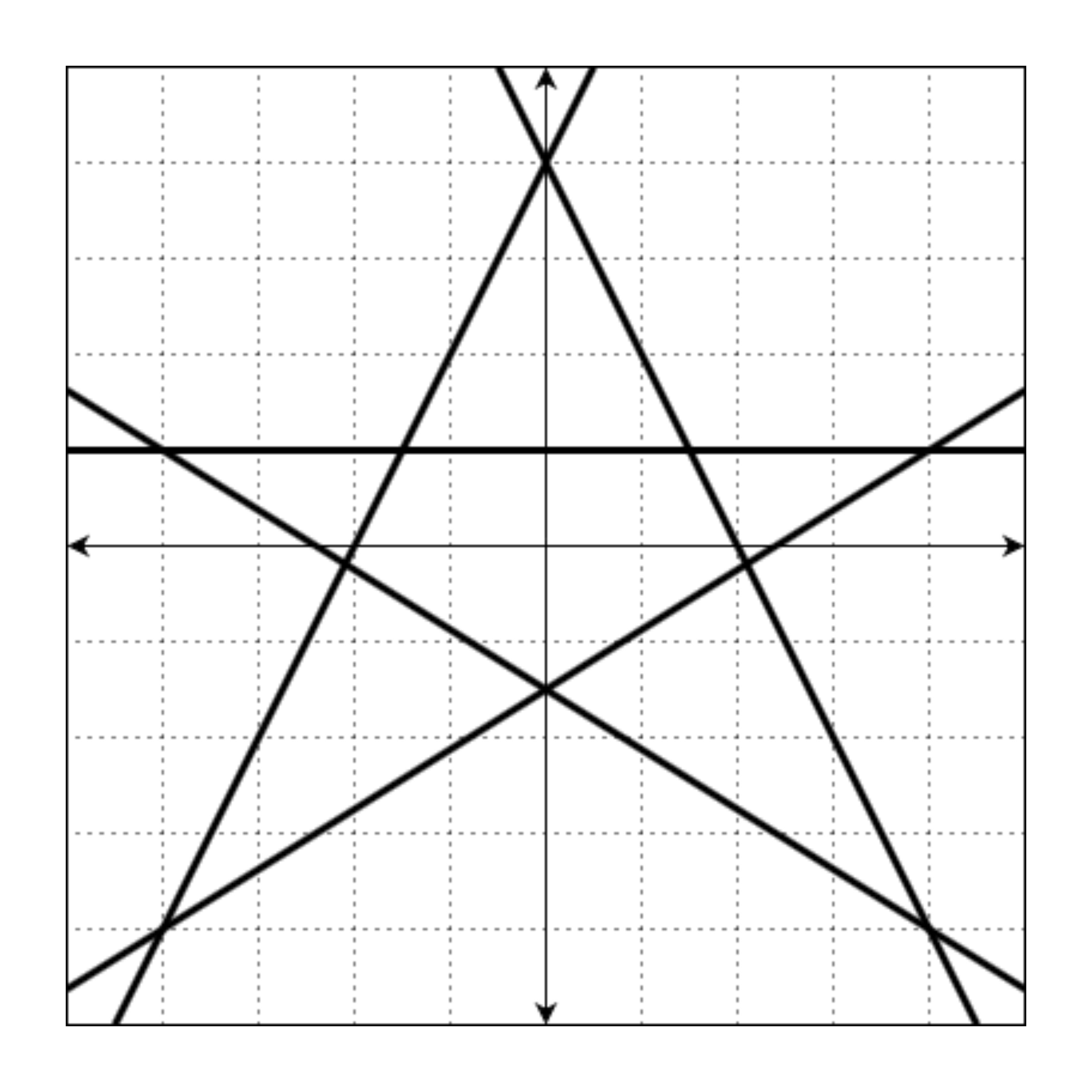
이때, 모든 교점의 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4), (1.5, 1.0), (2.1, -0.19), (0, -1.5), (-2.1, -0.19), (-1.5, 1.0)입니다. 이 중 정수로만 표현되는 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4)입니다.

만약 정수로 표현되는 교점에 별을 그리면 다음과 같습니다.

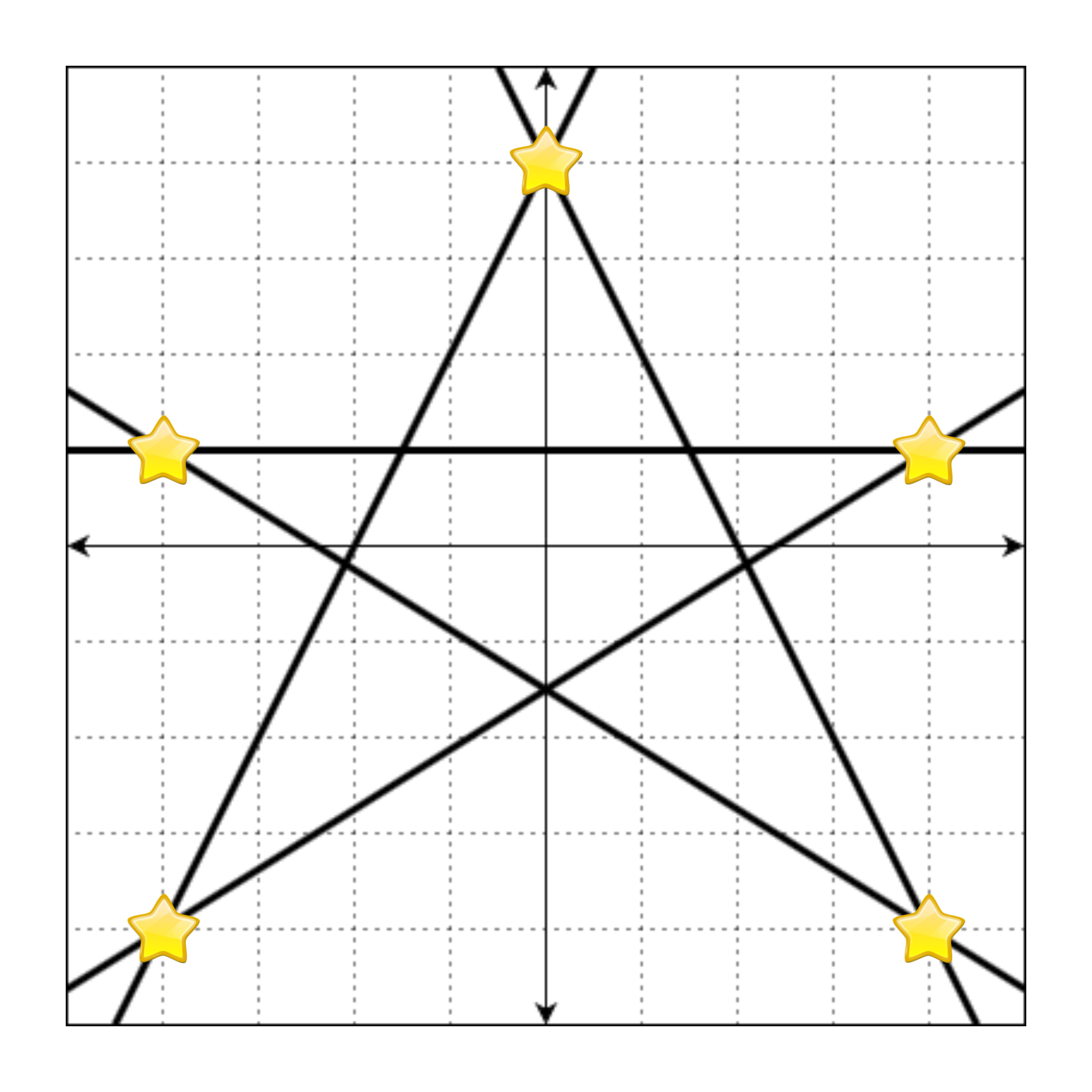
위의 그림을 문자열로 나타낼 때, 별이 그려진 부분은 *, 빈 공간(격자선이 교차하는 지점)은 .으로 표현하면 다음과 같습니다.

"..........."  
".....*....."  
"..........."  
"..........."  
".*.......*."  
"..........."  
"..........."  
"..........."  
"..........."  
".*.......*."  
"..........."  

이때 격자판은 무한히 넓으니 모든 별을 포함하는 최소한의 크기만 나타내면 됩니다.

따라서 정답은

"....*...."  
"........."  
"........."  
"*.......*"  
"........."  
"........."  
"........."  
"........."  
"*.......*"  

입니다.

직선 A, B, C에 대한 정보가 담긴 배열 line이 매개변수로 주어집니다. 이때 모든 별을 포함하는 최소 사각형을 return 하도록 solution 함수를 완성해주세요.

제한 사항

• line의 세로(행) 길이는 2 이상 1,000 이하인 자연수입니다.
  • line의 가로(열) 길이는 3입니다.
  • line의 각 원소는 [A, B, C] 형태입니다.
  • A, B, C는 -100,000 이상 100,000 이하인 정수입니다.
  • 무수히 많은 교점이 생기는 직선 쌍은 주어지지 않습니다.
  • A = 0이면서 B = 0인 경우는 주어지지 않습니다.
• 정답은 1,000 * 1,000 크기 이내에서 표현됩니다.
• 별이 한 개 이상 그려지는 입력만 주어집니다.

입출력 예

line	result
[[2, -1, 4], [-2, -1, 4], [0, -1, 1], [5, -8, -12], [5, 8, 12]]	["........", ".........", ".........", ".......", ".........", ".........", ".........", ".........", ".......*"]
[[0, 1, -1], [1, 0, -1], [1, 0, 1]]	["."]
[[1, -1, 0], [2, -1, 0]]	["*"]
[[1, -1, 0], [2, -1, 0], [4, -1, 0]]	["*"]

참고 사항
Ax + By + E = 0
Cx + Dy + F = 0
두 직선의 교점이 유일하게 존재할 경우, 그 교점은 다음과 같습니다

또, AD - BC = 0인 경우 두 직선은 평행 또는 일치합니다.

2. 풀이

계획1 - 문제에 나온 공식대로 모든 정수 교차점과 좌표의 최대/최솟값을 구합니다.

for (let i = 0; i < N - 1; i++) {
    for (let j = i + 1; j < N; j++) {
        const [a, b, e] = line[i];
        const [c, d, f] = line[j];

        const mod = a * d - b * c;
        if (!mod) continue; // 분모가 0인 경우 -> 서로 평행하거나 일치

        const xNumerator = b * f - e * d;
        const yNumerator = e * c - a * f;
        if (xNumerator % mod || yNumerator % mod) continue; // 정수가 아닌 교차점

        const x = xNumerator / mod;
        const y = yNumerator / mod;

        crossPoints.push([x, y]); // 교차점 추가
        minX = Math.min(minX, x); // 좌표 최대/최솟값 갱신
        minY = Math.min(minY, y);
        maxX = Math.max(maxX, x);
        maxY = Math.max(maxY, y);
    }
}

한 선분에 대해서 다른 모든 선분과 비교하며 교차점을 계산합니다.

계획2 - 너비와 높이를 계산 후, 별을 찍습니다.

const paper = [...Array(maxY - minY + 1)].map(() => [...Array(maxX - minX + 1)].map(() => '.'));

crossPoints.forEach(([x, y]) => {
    paper[maxY - y][x - minX] = '*';
});

높이는 maxY - minY + 1가 되고 너비는 maxX - minX + 1가 됩니다.
별을 찍을 때는 그래프 안에 있는 점들을 1사분면에 옮긴다 생각하시면 되는데
그 이유는 컴퓨터의 2차원 배열이 그래프의 1사분면을 뒤집은 형태로 표현되기 때문입니다.
그래서 y좌표 = maxY - y, x좌표 = x - minX의 결과가 나옵니다.
조금만 생각해보면 그리 어렵지 않습니다.

3. 전체 코드

function solution(line) {
    const N = line.length;
    const INF = Number.MAX_SAFE_INTEGER;
    const crossPoints = [];
    let minX = INF;
    let minY = INF;
    let maxX = -INF;
    let maxY = -INF;

    // 계획1 - 문제에 나온 공식대로 모든 정수 교차점과 좌표의 최대/최솟값을 구합니다.
    for (let i = 0; i < N - 1; i++) {
        for (let j = i + 1; j < N; j++) {
            const [a, b, e] = line[i];
            const [c, d, f] = line[j];

            const mod = a * d - b * c;
            if (!mod) continue; // 분모가 0인 경우 -> 서로 평행하거나 일치

            const xNumerator = b * f - e * d;
            const yNumerator = e * c - a * f;
            if (xNumerator % mod || yNumerator % mod) continue; // 정수가 아닌 교차점

            const x = xNumerator / mod;
            const y = yNumerator / mod;

            crossPoints.push([x, y]); // 교차점 추가
            minX = Math.min(minX, x); // 좌표 최대/최솟값 갱신
            minY = Math.min(minY, y);
            maxX = Math.max(maxX, x);
            maxY = Math.max(maxY, y);
        }
    }

    // 계획2 - 너비와 높이를 계산 후, 별을 찍습니다.
    const paper = [...Array(maxY - minY + 1)].map(() => [...Array(maxX - minX + 1)].map(() => '.'));

    crossPoints.forEach(([x, y]) => {
        paper[maxY - y][x - minX] = '*';
    });

    return paper.map(v => v.join(''));
}