1. 문제
설명
계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.
아래 그림은 m = 4, n = 3 인 경우입니다.
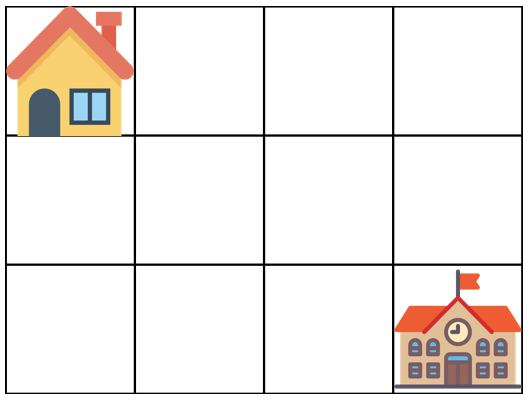
가장 왼쪽 위, 즉 집이 있는 곳의 좌표는 (1, 1)로 나타내고 가장 오른쪽 아래, 즉 학교가 있는 곳의 좌표는 (m, n)으로 나타냅니다.
격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 격자의 크기 m, n은 1 이상 100 이하인 자연수입니다.
* m과 n이 모두 1인 경우는 입력으로 주어지지 않습니다. - 물에 잠긴 지역은 0개 이상 10개 이하입니다.
- 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않습니다.
입출력 예
| m | n | puddles | return |
|---|---|---|---|
| 4 | 3 | [[2, 2]] | 4 |
2. 풀이
2-1. 완전 탐색
늘 그랬듯이 먼저 완전 탐색으로 접근해봅시다.
집에서 학교로 가는 모든 경로를 탐색해서
학교에 도착할 수 있는 경우를 카운팅하면 됩니다.
// 모든 경로를 탐색하는 함수
static public int f(int y, int x) {
// 도착했을 때 1을 반환
if (y == N && x == M) return 1;
int ret = 0;
// 아래로 갈 수 있을 때
if (y + 1 <= N && map[y + 1][x] != -1) ret = (ret + f(y + 1, x)) % MOD;
// 오른쪽으로 갈 수 있을 때
if (x + 1 <= M && map[y][x + 1] != -1) ret = (ret + f(y, x + 1)) % MOD;
return ret;
}실행 결과
이 재귀 함수는 우리의 예상대로 잘 동작합니다만, 문제는 역시 효율성이죠.
격자의 크기는 n x m이고 각 격자마다 오른쪽, 아래쪽으로 가는 경우를 모두 탐색하니
시간 복잡도는 O(2^nm)이 됩니다. 어마무시하죠...
이 때 사용하는 기법이 바로 메모이제이션입니다.
지난 포스팅에서 배운 방법대로 메모이제이션 기법을 사용해봅시다.
2-2. 메모이제이션
// dp[y][x] = (y, x)에서 (N, M)으로 가는 경로의 개수
static public int f(int y, int x) {
if (y == N && x == M) return 1;
if (dp[y][x] != -1) return dp[y][x];
int ret = 0;
if (y + 1 <= N && map[y + 1][x] != -1) ret = (ret + f(y + 1, x)) % MOD;
if (x + 1 <= M && map[y][x + 1] != -1) ret = (ret + f(y, x + 1)) % MOD;
return dp[y][x] = ret;
}실행 결과
어떻습니까? 코드는 별로 수정하지 않았지만 메모이제이션 기법 하나로
효율성 테스트를 모두 통과했습니다.
시간 복잡도는 dp배열을 채우는데 비례하니 O(nm)이 되기 때문이죠.
2-3. bottom-up
지금까지 재귀 함수를 이용해서 풀었는데 반복문으로도 깔끔하게 짤 수 있습니다.
아니 오히려 더 깔끔하게 짤 수 있습니다.
bottom-up기법은 초기값을 잘 잡은 다음
메모이제이션에서 나온 점화식을 반대로 적용해주면 됩니다.
// dp[i][j] = (1, 1)에서 (i, j)까지 갈 수 있는 경우의 수
class Solution {
public int solution(int m, int n, int[][] puddles) {
int[][] dp = new int[n + 1][m + 1];
int[][] map = new int[n + 1][m + 1];
// 웅덩이 설정
for (int[] p: puddles)
map[p[1]][p[0]] = -1;
// 초기값 설정
// dp[i][j]의 정의상 'dp[1][1] = 1'이 맞지만
// 반복문을 깔끔하게 짜기 위해 'dp[0][1] = 1'로 설정했습니다.
dp[0][1] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 현 위치가 웅덩이일 땐 넘어감
if (map[i][j] == -1) continue;
// dp[i][j] = dp[i - 1][j]까지 갈 수 있는 경우의 수 + dp[i][j - 1]까지 갈 수 있는 경우의 수
dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % 1000000007;
}
}
return dp[n][m];
}
}