백준 - 휴계소 세우기 (1477)

1. 문제 링크

문제 링크

2. 풀이

전형적인 parametric search 문제입니다.
반복문으로 l - 1부터 1까지 간격을 설정한 다음,
그 간격으로 휴계소를 세워서 m개를 세울 수 있다면 답이 됩니다.
즉 특정 간격 이하부터는 m개 이상으로 세울 수 있고
간단하게 그래프로 그려보면 아래와 같습니다.

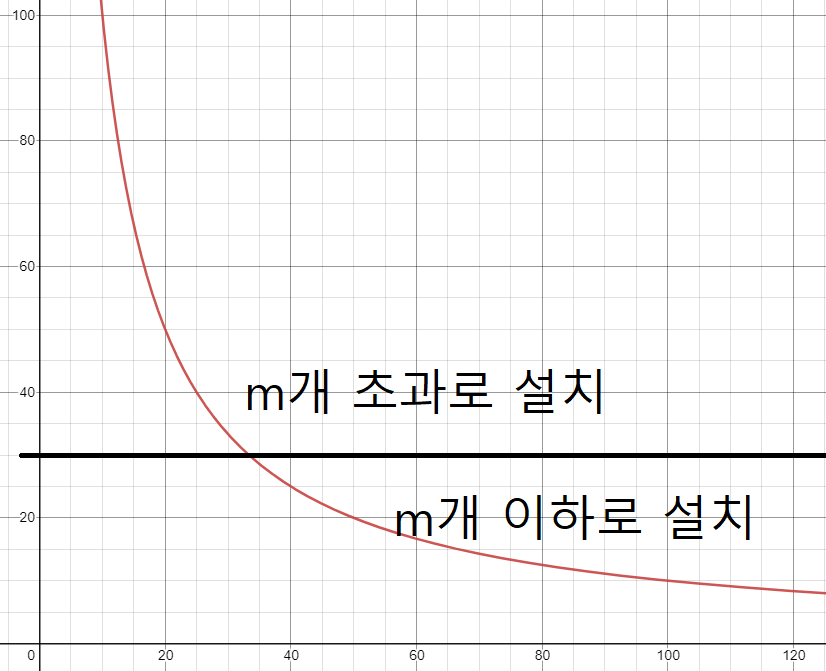
• Y축 - 휴계소 사이의 거리의 최댓값
• X축 - 휴계소 사이의 거리의 최솟값

검정색 수평선 위로는 m개 초과로 설치
검정색 수평선을 포함한 아래는 m개 이하로 설치한 경우입니다.
즉,
최적화 문제 - 휴계소 m개를 설치할 때 휴계소 사이의 거리의 최댓값
결정 문제 - 휴계소 사이의 거리의 최솟값이 mid일 때 휴계소 m개를 세울 수 있는가?
로 바꿀 수 있다는 의미입니다.

1. 구간 설정

sort(a + 1, a + 1 + n);
a[0] = 0;
a[n + 1] = l;

int lo = 0, hi = l;

정답의 범위는 1부터 l - 1까지 나올 수 있으니lo = 1, hi = l로 설정합니다.
마찬가지로 휴계소도 1부터 l - 1까지 세울 수 있으니
첫 번째 인덱스는 0, 마지막 인덱스는 l로 설정합니다.

2. 결정 함수 만들기

bool check(int inter) {
	int cnt = 0;

	for (int i = 1; i <= n + 1; i++) {
		cnt += (a[i] - a[i - 1] - 1) / inter;
	}

	return cnt > m;
}

휴계소를 세울 수 있는 위치는 a[i] - 1부터 a[i - 1] + 1까지 입니다.
이로서 도출되는 휴계소를 세울 수 있는 길이의 식은
(a[i] - 1) - (a[i - 1] + 1) - 1이 되고, 간단화하면 a[i] - a[i - 1] - 1이 됩니다.
위 식을 현재 간격으로 나누면 세울 수 있는 휴계소의 개수를 얻을 수 있습니다.

3. 파라메트릭 서치 실행

while (lo + 1 < hi) {
	int mid = (lo + hi) / 2;

	if (check(mid)) lo = mid;
	else hi = mid;
}

cout << hi;

세울 수 있는 휴계소의 개수가 m보다 크다면
구간의 크기를 늘려서 m개로 맞춰야 하므로 lo = mid,
세울 수 있는 휴계소의 개수가 m보다 작거나 같다면
구간의 크기를 줄여서 m개로 맞춰야 하므로 hi = mid 가 됩니다.

그리고 정답의 범위인 작거나 같다면에 해당하는 hi가 답이 됩니다.
위의 그래프로 따지면 hi는 검정색 수평선에 해당하는 x값이 됩니다.

3. 전체 코드

#define MAX 55
#include <bits/stdc++.h>

using namespace std;

int n, m, l;
int a[MAX];

bool check(int inter) {
	int cnt = 0;

	for (int i = 1; i <= n + 1; i++) {
		cnt += (a[i] - a[i - 1] - 1) / inter;
	}

	return cnt > m;
}

int main(void) {
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n >> m >> l;

	for (int i = 1; i <= n; i++) cin >> a[i];

	sort(a + 1, a + 1 + n);
	a[0] = 0;
	a[n + 1] = l;

	int lo = 0, hi = l;

	while (lo + 1 < hi) {
		int mid = (lo + hi) / 2;

		if (check(mid)) lo = mid;
		else hi = mid;
	}

	cout << hi;

	return 0;
}