프로그래머스 - 표 편집

1. 문제

문제 링크

설명

업무용 소프트웨어를 개발하는 니니즈웍스의 인턴인 앙몬드는 명령어 기반으로 표의 행을 선택, 삭제, 복구하는 프로그램을 작성하는 과제를 맡았습니다. 세부 요구 사항은 다음과 같습니다

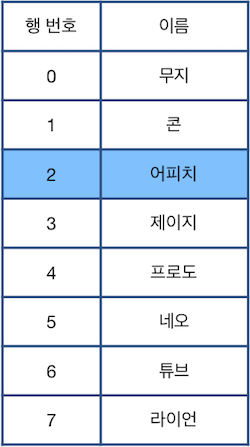
위 그림에서 파란색으로 칠해진 칸은 현재 선택된 행을 나타냅니다. 단, 한 번에 한 행만 선택할 수 있으며, 표의 범위(0행 ~ 마지막 행)를 벗어날 수 없습니다. 이때, 다음과 같은 명령어를 이용하여 표를 편집합니다.

• "U X": 현재 선택된 행에서 X칸 위에 있는 행을 선택합니다.
• "D X": 현재 선택된 행에서 X칸 아래에 있는 행을 선택합니다.
• "C" : 현재 선택된 행을 삭제한 후, 바로 아래 행을 선택합니다. 단, 삭제된 행이 가장 마지막 행인 경우 바로 윗 행을 선택합니다.
• "Z" : 가장 최근에 삭제된 행을 원래대로 복구합니다. 단, 현재 선택된 행은 바뀌지 않습니다.

예를 들어 위 표에서 "D 2"를 수행할 경우 아래 그림의 왼쪽처럼 4행이 선택되며, "C"를 수행하면 선택된 행을 삭제하고, 바로 아래 행이었던 "네오"가 적힌 행을 선택합니다(4행이 삭제되면서 아래 있던 행들이 하나씩 밀려 올라오고, 수정된 표에서 다시 4행을 선택하는 것과 동일합니다).

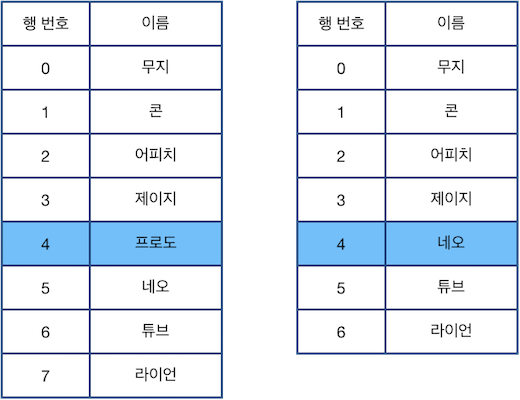
다음으로 "U 3"을 수행한 다음 "C"를 수행한 후의 표 상태는 아래 그림과 같습니다.

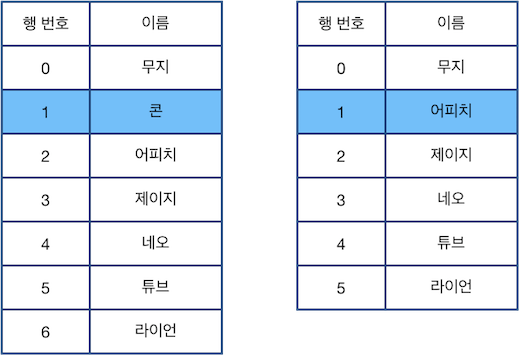
다음으로 "D 4"를 수행한 다음 "C"를 수행한 후의 표 상태는 아래 그림과 같습니다. 5행이 표의 마지막 행 이므로, 이 경우 바로 윗 행을 선택하는 점에 주의합니다.

다음으로 "U 2"를 수행하면 현재 선택된 행은 2행이 됩니다.

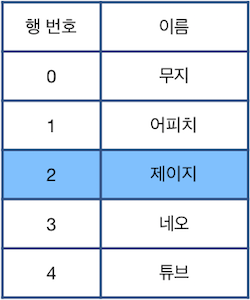
위 상태에서 "Z"를 수행할 경우 가장 최근에 제거된 "라이언"이 적힌 행이 원래대로 복구됩니다.

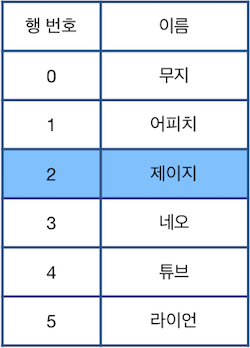
다시한번 "Z"를 수행하면 그 다음으로 최근에 제거된 "콘"이 적힌 행이 원래대로 복구됩니다. 이때, 현재 선택된 행은 바뀌지 않는 점에 주의하세요.

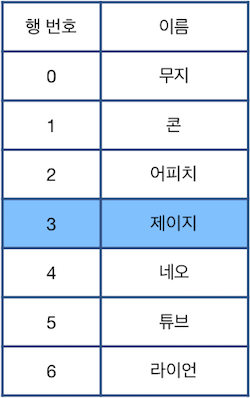
이때, 최종 표의 상태와 처음 주어진 표의 상태를 비교하여 삭제되지 않은 행은 "O", 삭제된 행은 "X"로 표시하면 다음과 같습니다.

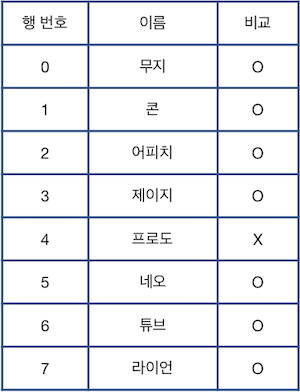
처음 표의 행 개수를 나타내는 정수 n, 처음에 선택된 행의 위치를 나타내는 정수 k, 수행한 명령어들이 담긴 문자열 배열 cmd가 매개변수로 주어질 때, 모든 명령어를 수행한 후 표의 상태와 처음 주어진 표의 상태를 비교하여 삭제되지 않은 행은 O, 삭제된 행은 X로 표시하여 문자열 형태로 return 하도록 solution 함수를 완성해주세요.

입출력 예

n	k	cmd	result
8	2	["D 2","C","U 3","C","D 4","C","U 2","Z","Z"]	"OOOOXOOO"
8	2	["D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C"]	"OOXOXOOO"

2. 풀이

단순 배열 활용

js 기준으로 Array.splice 메서드를 사용할 때

• C명령을 하면 내부적으로 인덱스를 한 칸씩 앞당기기 (삭제 연산) -> O(n)소요
• Z명령을 하면 내부적으로 인덱스를 한 칸씩 밀기 (중간 삽입 연산) -> O(n)소요

위와 같이 구현되어 있기 때문에 효율성 검사에서 통과하지 못할 겁니다.

더블 링크드 리스트 활용

이런 문제는 사실 보자마자 링크드 리스트 떠올려야 됩니다.
삽입, 삭제가 빈번하게 일어나는 문제는 무조건 링크드 리스트입니다.
이 문제에서는 U명령과 D명령을 통해 위, 아래로 이동할 수 있기 때문에
더블 링크드 리스트가 필요합니다.

스택 활용

더블 링크드 리스트 말고도 필요한 자료구조가 하나 더 있습니다.
Z명령을 수행할 때 쓰이는 스택입니다.
문제에서 보다시피 가장 최근에 C명령으로 삭제된 행이 Z명령으로 복구되기 때문에
스택에 삭제된 행을 담아두고, pop하면서 더블 링크드 리스트에 복구시키면 됩니다.

z 명령 수행시 주의점

그래도 많은 분들이 더블 링크드 리스트와 스택의 활용 문제라는 사실은 알고 계셨을 겁니다.
저도 처음 풀이시에 두 자료구조를 활용하여 이동, 삽입, 삭제를 하며 풀이했지만
효율성 검사해서 통과하지 못했습니다.
더블 링크드 리스트의 원소들은 무조건 오름차순을 유지하고 있기 때문에
z명령을 수행할 때 pop된 행의 값을 더블 링크드 리스트의 앞에서부터 순차적으로 따라가며
오름차순을 유지할 수 있는 위치를 찾은 다음에 삽입 연산을 했기 때문에 그렇습니다.

'역시 효율성 통과 못하는 구나' 깨닫고
Z명령의 성능 개선을 위해 그림을 그려본 결과, 놀라운 사실을 알아냈습니다.

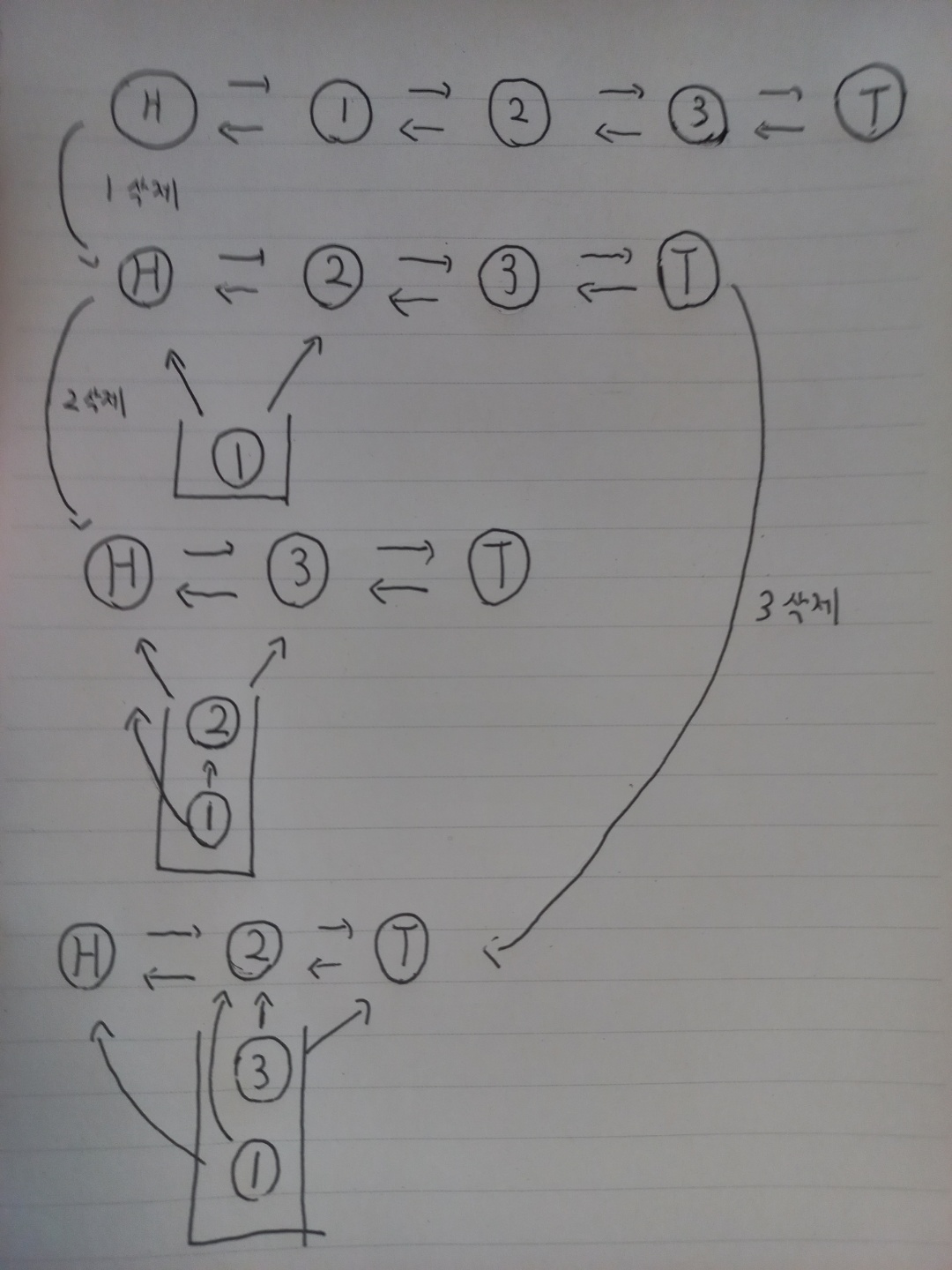
삭제된 행들은 더블 링크드 리스트의 원소들을 못 잊고 가리키고 있었습니다.
그리고 가장 최근에 삭제된 행이 먼저 복구되기 때문에 언제든지 원래 모양으로 되돌아갈 수 있습니다.
이로서 스택에서 pop해온 원소를 node라고 칭할 때

node.prev.next = node;
node.next.prev = node;

위 코드로만 Z명령을 구현할 수 있기 때문에 O(1)만에 복구가 됩니다.
저는 이 때 유레카!를 외쳤답니다. ㅋㅋ

3. 전체 코드

class DoubleLinkedList {
    constructor() {
        this.head = this.initNode(null);
        this.tail = this.initNode(null);

        this.head.next = this.tail;
        this.tail.prev = this.head;
    }

    initNode(data) {
        return {
            data,
            prev: null,
            next: null,
        };
    }

    move(node, count, dir) {
        while (count--) {
            node = node[dir];
        }

        return node;
    }
	
    // 오른쪽으로 이동 (D명령)
    moveRight(node, count) {
        return this.move(node, count, 'next');
    }

    // 왼쪽으로 이동 (U명령)
    moveLeft(node, count) {
        return this.move(node, count, 'prev');
    }
    
    // 꼬리에 추가
    addToTail(data) {
        const node = this.initNode(data);

        this.tail.prev.next = node;
        node.prev = this.tail.prev;
        node.next = this.tail;
        this.tail.prev = node;
    }

    // 삭제 연산 (D 명령)
    remove(node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
        
        // 가장 마지막 행일 땐 이전 원소 
        return node[node.next != this.tail ? 'next' : 'prev'];
    }

    // 복구 연산 (Z 명령)
    recover(node) {
        node.prev.next = node;
        node.next.prev = node;
    }
}

class Stack {
    constructor() {
        this.top = this.initNode(null);
    }

    initNode(data) {
        return {
            data,
            next: null,
        };
    }

    push(data) {
        const node = this.initNode(data);
        node.next = this.top;
        this.top = node;
    }

    pop() {
        const node = this.top;
        
        this.top = node.next;

        return node.data;
    }
}

function solution(n, k, cmd) {
    const table = new DoubleLinkedList();
    const st = new Stack();
    const ans = [...Array(n)].map(() => 'X');

    for (let i = 0; i < n; i++) {
        table.addToTail(i);
    }

    let cur = table.moveRight(table.head.next, k);

    cmd.forEach(v => {
        const [c, num] = v.split(' ');

        if (c == 'D') {
            cur = table.moveRight(cur, Number(num));
        } else if (c == 'U') {
            cur = table.moveLeft(cur, Number(num));
        } else if (c == 'C') {
            st.push(cur);
            cur = table.remove(cur);
        } else {
            table.recover(st.pop());
        }
    });

    cur = table.head.next;

    // 더블 링크드 리스트에 남은 애들은 현재 남아있는 행들이니, 차례대로 순회하며 'O' 표시
    while (cur != table.tail) {
        ans[cur.data] = 'O';
        cur = table.moveRight(cur, 1);
    }

    return ans.join('');
}

효율성 문제인만큼 스택도 구현해봤습니다.
js의 Array.push연산은 내부적으로 새배열을 만들어서 복사하기 때문에 효율성이 떨어집니다.