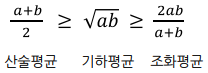[230220-24] 머신러닝에 앞선 통계, 모델 성능 평가, 모델링 기본 코드

지도학습에만 대해서 배웠음

• 지도학습: 학습 대상이 되는 데이터에 정답을 주고 규칙성, 데이터의 패턴을 배우게 하는 것
  • 그 중에서도 분류와 회귀에 대해서 배움
    • 분류인지 회귀인지 구분을 잘해야 함
    • 회귀는 연속적인 숫자를 예측, 아니면 분류

• 데이터 셋을 실제로는 학습용/검증용/평가용 데이터로 구분하는 데, 수업에는 학습용/평가용으로 할거임

• 과대적합 (Overfitting) : 학습데이터에서만 너무 잘 맞아서 실전에서는 예측 성능 별로
• 과소적합 (Underfitting) : 모델 너무 단순해서 훈련이 안되었거나, 평가 데이터 점수가 더 높거나, 둘다 점수가 낮거나

• $Scikit-Learn$ (사이킷런 라이브러리) :
  오픈소스, 같은 구조의 코드로 여러 알고리즘 가능, 토이 데이터 셋 포함

---

머신러닝을 위한 통계

성능평가 - 회귀 모델 성능 평가 (오차를 줄이자)

• $SSE$ (Sum Squared Error) : 오차 제곱의 합
• $MSE$ (Mean SSE) : 오차 제곱의 평균
• $RMSE$ (Root MSE) : 오차 제곱의 평균의 루트, 제곱근
  
  
• $MAE$ (Mean Absloute Error) : 오차 절대값의 평균
  
  
• $MAPE$ (Mean Absolute Percentage Error) : 평균 절대 백분율 오차, 예측 방법의 예측 정확도를 측정
  
  
  

  $SST$(전체오차 제곱합) = $SSE$( |평균-예측| $^2$ ) + $SSR$( |예측-실제| $^2$ )

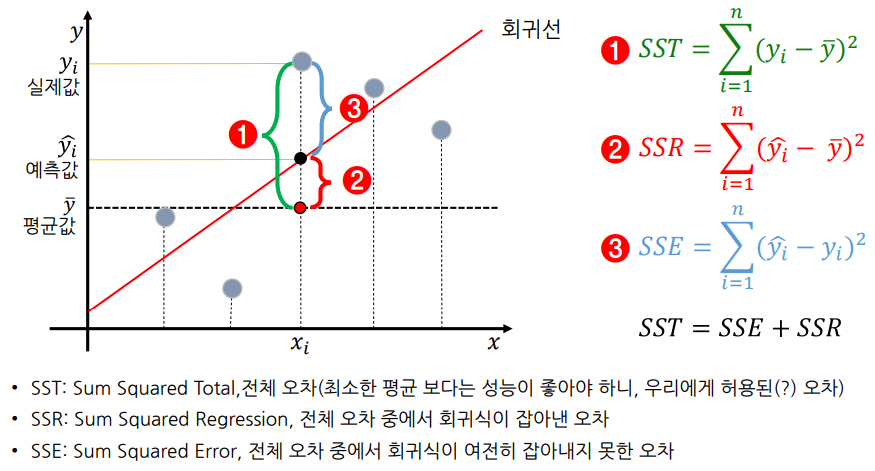
• 결정 계수 $R^2$ (R-Squared) :
  - $MSE$를 표준화하여 모델 성능을 잘 해석하기 위함
  - 전체 오차 중에서 회귀식이 잡아낸 오차 비율 (일반적으로 0 ~ 1 사이임)
  - 오차의 비, 설명력이라고도 함
  - $R^2 = 1$ 이면 $MSE = 0$이고 모델이 데이터를 완벽하게 학습한 것임

  $R^2 = \cfrac{SSR}{SST} = 1 - \cfrac{SSE}{SST}$

성능평가 - 분류 모델 성능 평가 (정확도를 높이자)

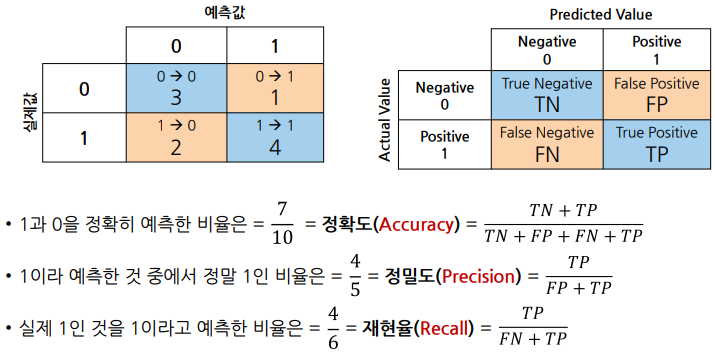
• $Accuracy$ (정확도, 정분류율) $= \cfrac{TN + TP}{TN + FP + FN + TP}$
  ㄴ 1과 0을 정확히 예측한 비율
  
  
• $Precision$ (정밀도) $= \cfrac{TP}{FP + TP}$
  ㄴ 1이라 예측한 것 중에 실제 1인 비율
  ㄴ 정밀도 낮을 경우 : 비 안오는데 온다고 해서 불필요한 우산을 챙기게 됨, 암 아닌데 암이라 해서 불필요한 치료 발생
  
  
• $Recall$ (재현율) $= \cfrac{TP}{FN + TP}$
  ㄴ 실제 1인 것을 1이라고 예측한 비율
  ㄴ 재현율 낮을 경우 : 비가 내리는데 안내린다고 해서 비를 맞게 됨, 암인데 암 아니라 해서 심각한 결과 초래
  
  
• $Specificity$ (특이도) $= \cfrac{TN}{TN + FP}$
  ㄴ 실제 0인 것을 0이라고 예측한 비율
  ㄴ 특이도 낮을 경우 : 비 안오는데 온다고 해서 불필요한 우산을 챙기게 됨, 암 아닌데 암이라 해서 불필요한 치료 발생
  
  
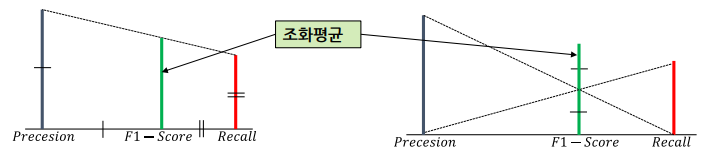
• $F1-Score$ (정밀도와 재현율의 조화평균)
  $= 2 \times \cfrac{1}{\cfrac{1}{Precesion} + \cfrac{1}{Recall}} = \cfrac{2 \times Precesion \times Recall}{Precesion + Recall}$
  
  
  ㄴ 작은 값 쪽으로 치우친, 작은 값과 큰 값 사이의 값을 가진 평균
  ㄴ 산술평균보다 큰 값이 끼치는 영향이 줄어듦

---

< 데이터 준비 >

1. 결측치 확인 및 처리

data.isna().sum()

# 전날 값으로 채우기
data.fillna(method = 'ffill', inplace = True)

# NaN 이 포함된 모든 행(axis = 0) 제거
data.dropna(axis=0, inplace=True)

2. 변수 제거 - 분석 의미 없는거 버리기

drop_cols = ['Month', 'Day']
data.drop(drop_cols, axis = 1, inplace = True)

3. x, y 분리

# target 확인
target = 'Ozone'

# 데이터 분리
x = data.drop(target, axis = 1)
y = data.loc[:, target]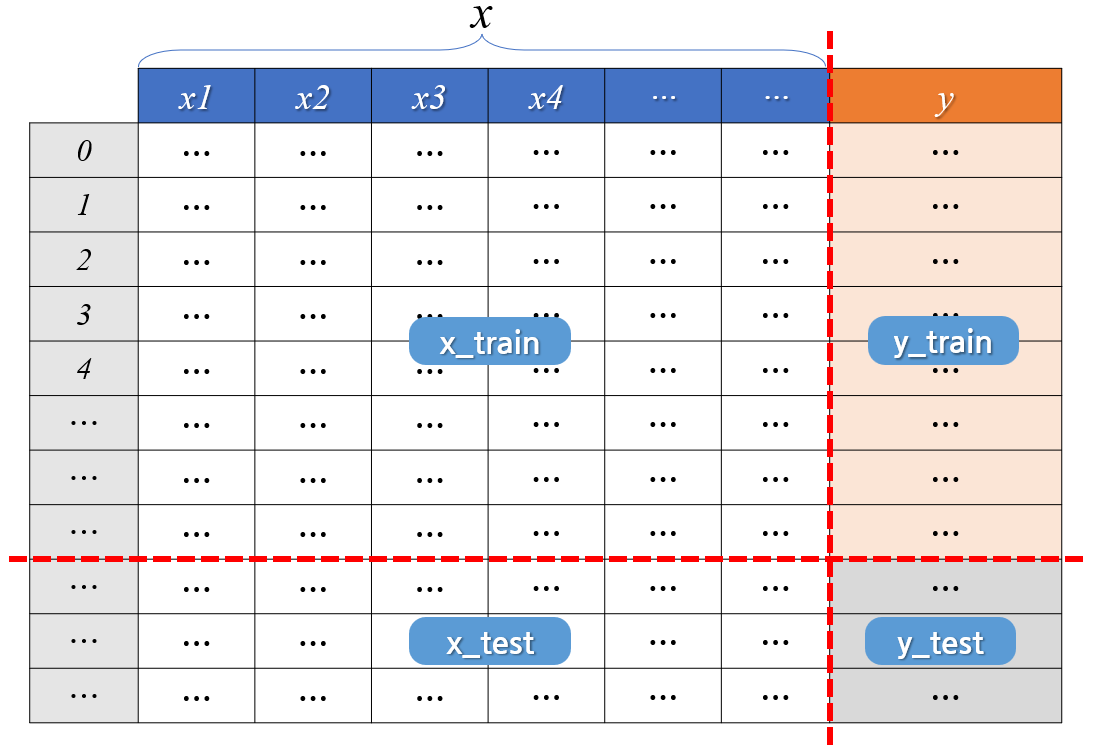

# 모듈 불러오기
from sklearn.model_selection import train_test_split

# 7:3으로 분리
x_train, x_test, y_train, y_test = train_test_split(
                                   x, y, test_size = 0.3, random_state = 1)
# random_state는 호출할 때마다 동일한 학습/테스트용 데이터를 생성하기 위해 주어지는 난수 값

< 모델링 기본 코드 >

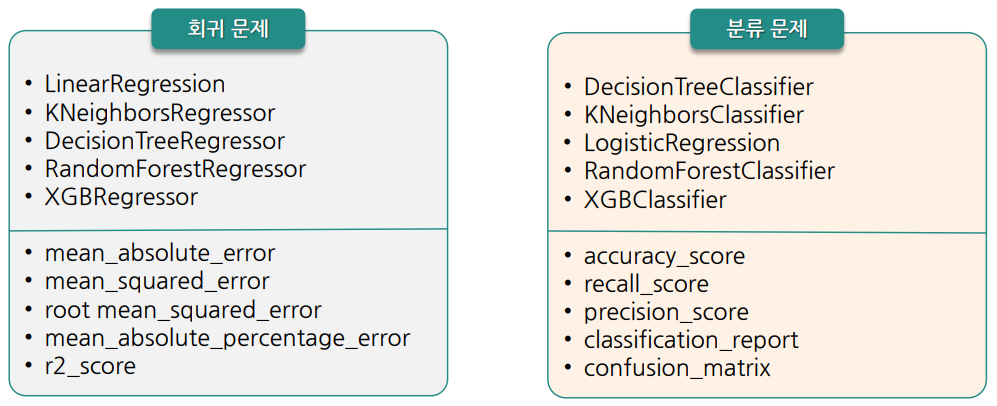
• 회귀 문제 or 분류 문제? => 알고리즘과 평가 방법이 달라짐
  • 예시 : 알고리즘 - LinearRegression, 평가방법 - mean_absolute_error

1. 불러오기

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error

2. 선언하기

model = LinearRegression()

3. 학습하기

model.fit(x_train, y_train)

4. 예측하기

y_pred = model.predict(x_test)

5. 결과확인

print(y_test.values[:10]) # 왼 인덱스, 오 밸류
print(y_pred[:10])

6. 평가하기

print('MAE', mean_absolute_error(y_test, y_pred))

7. 결과 시각화

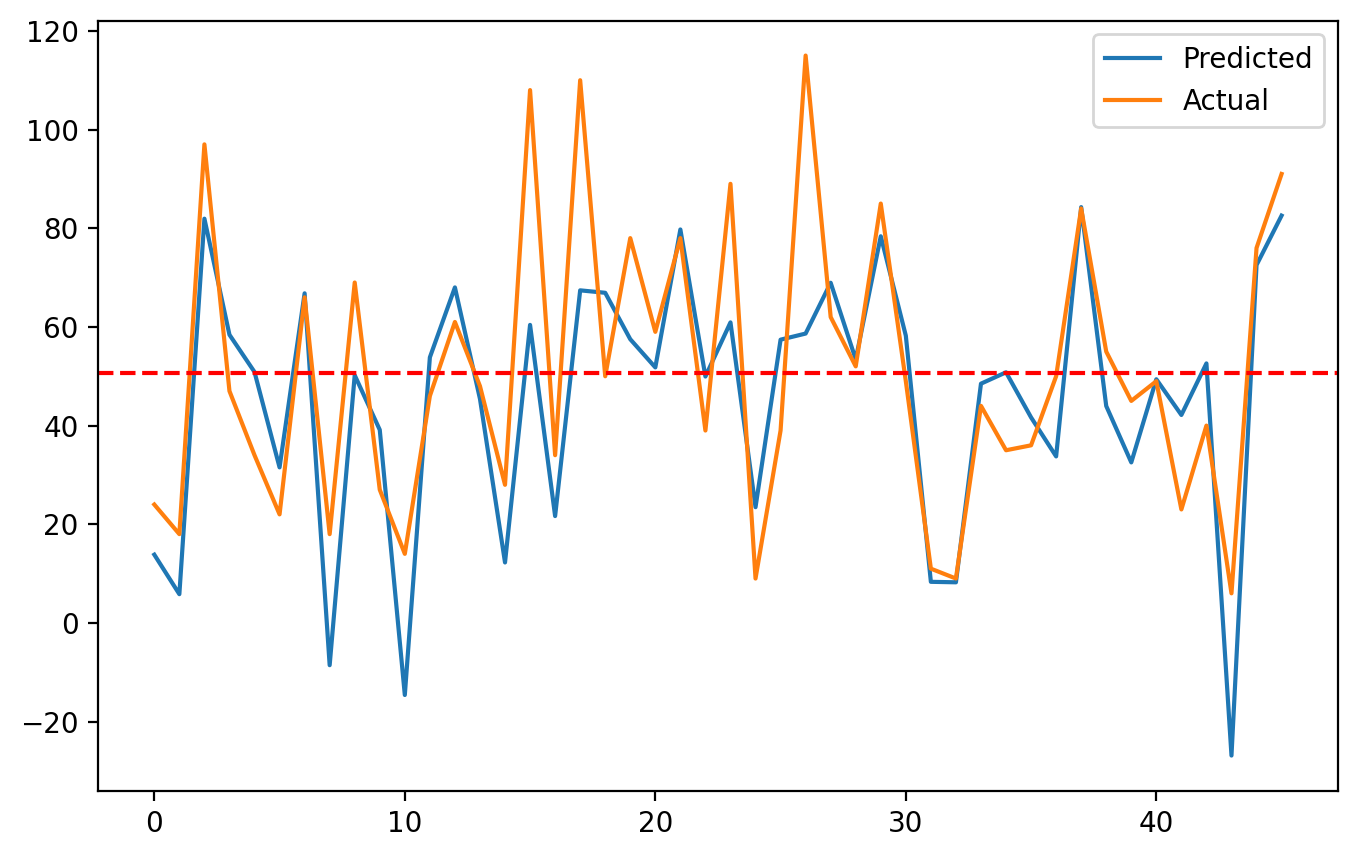
ozone_mean = y_test.mean()

plt.figure(figsize = (8, 5))
plt.plot(y_pred, label = 'Predicted')
plt.plot(y_test.values, label = 'Actual')
plt.axhline(ozone_mean, color = 'r', linestyle = '--')
plt.legend()
plt.show()