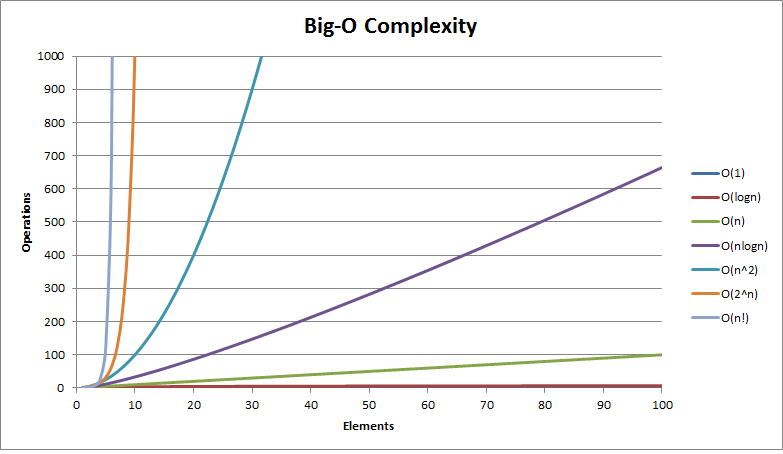
시간 복잡도, Time complexity
- 입력 값 n에 대하여 하나의 결과 값을 도출하는데 다양한 로직을 구현할 수 있다.
- 입력 값 n에 대하여 문제를 해결하는데 로직에 따라 걸리는 실행 시간을 시간 복잡도라고 한다.
Big-O 표기법, 대문자 O 표기법
- O(1), 상수 시간, Constant time : 한번의 연산 과정으로 결과 값 반환
function constantTime(arr, n) {
return arr[n]
}O(1)은 어떠한 Input값을 받든 실행 시간은 항상 같다.
- O(n), 직선적 시간 Linear time : 실행 시간이 Input, 입력 값의 크기와 같다. 따라서 Input값의 크기에 따라 실행 시간도 증가한다.
function linearTime(arr, callback) {
for(let i = 0; i < arr.length; i++) {
callback(arr[i], i, arr)
}
}배열에 접근해서 배열의 요소, index, 원본 배열을 callback 함수에 인자로 전달하는 함수이다. 배열의 요소만큼 실행 시간을 가진다.
- O(log n), 로그 시간, Logarithmic time : 특정 로직에 의해 문제 해결 단계를 줄여가며 입력 값의 단계를 줄이는 알고리즘에 비례 한다.
정렬된 배열에서 원소를 찾을 때 단순 for 문만을 활용하면 찾고자하는 원소를 찾을 때까지 배열의 길이 만큼 반복해야 한다(O(n)). 이는 배열의 크기가 커질수록 for 문의 실행시간이 늘어나 비 효율적인 시간 복잡도를 가진다. 따라서 순차적인 배열을 반으로 줄여가며 원소를 검사하는 로직을 구현하면 O(n)보다 효율적인 시간 복잡도를 가지게 할 수 있다.
function logarithmicTime(arr, n) {
// 배열의 첫번째, 중간, 마지막 요소 Index를 선언해준다.
let firstIndex = 0;
let lastIndex = arr.length - 1;
let midIndex;
// for 문 i의 초기화 값을 첫번째 index로, 마지막 index까지 돌려준다.
for(let i = firstIndex; i <= lastIndex; i++) {
// 배열의 중간 index를 할당해준다.
midIndex = Math.floor((firstIndex + lastIndex) / 2);
// 배열의 중간 index 요소와 n을 비교하고 n이 크면 firstIndex = midIndex, 작으면 lastIndex = midIndex로 초기화 시켜준다.
if(arr[midIndex] < n) {
firstIndex = midIndex + 1
} else if(arr[midIndex] > n) {
lastIndex = midIndex - 1
// 배열의 중간 index 요소와 n이 같으면 index를 반환하여 확인할 수 있다.
} else if(arr[midIndex] === n) {
return midIndex;
}
}
// 배열에 요소가 없다면 undefined를 반환한다.
return undefined;
}위 알고리즘은 Binary search algorithm으로 정렬된 배열이 주어졌을 때 배열 요소에 전부 접근하는 방식이 아닌 중간 index를 기준으로 반으로 줄여가며 찾고자 하는 요소의 n과 비교해 n의 index를 반환하는 함수로 로그 시간 복잡도를 가장 이해하기 좋은 대표적 예시이다.
-O(n^2), 2차 시간, Quadratic time : 문제를 해결하기 위해 입력 값 n의 제곱만큼의 단계의 수를 가지는 시간 복잡도.
function QuadraticTime(arr) {
for(let i = 0; i < arr.length; i++) {
for(let j = 0; j < arr.length; j++) {
if(i !== j && arr[i] === arr[j]) {
return true;
}
}
}
return false;
}위 함수는 배열안에 중복된 값이 있는지 확인하는 함수이다. 이 함수는 하나의 입력 값을 가지고 있지만 중복된 값을 확인하기 위해 하나의 입력 값을 두번 확인해야 한다.
- O(C^n), 지수 시간, Exponential time : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n 제곱.
function exponentialTime(num) {
if (num <= 1) return 1;
return exponentialTime(num - 1) + exponentialTime(num - 2);
}재귀를 통해 구현한 fibonacci 함수이다. 입력 값 num이 커지면 그 값의 n제곱만큼 연산 횟수가 증가한다.
Reference
https://medium.com/@ariel.salem1989/an-easy-to-use-guide-to-big-o-time-complexity-5dcf4be8a444
https://joshuajangblog.wordpress.com/category/algorithm-programming/
