프로그래머스 합승 택시 요금

피나코·2022년 1월 8일

알고리즘

목록 보기

18/46

문제 바로가기

문제

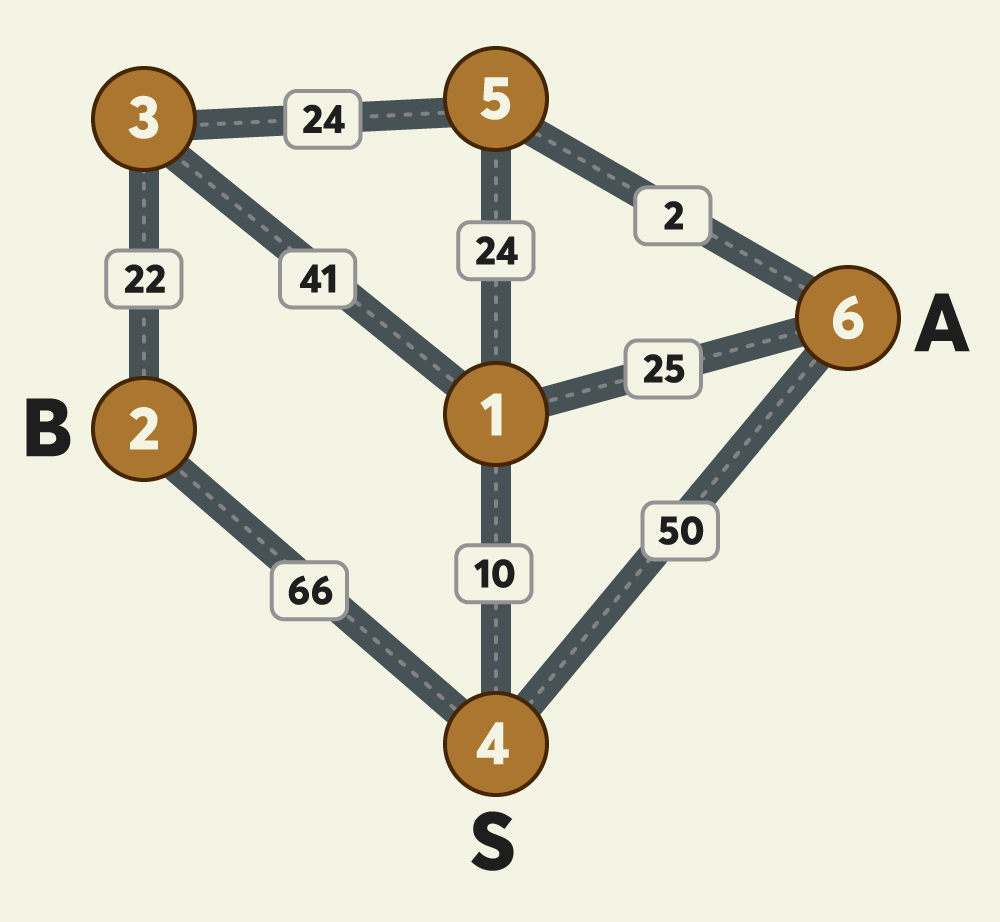
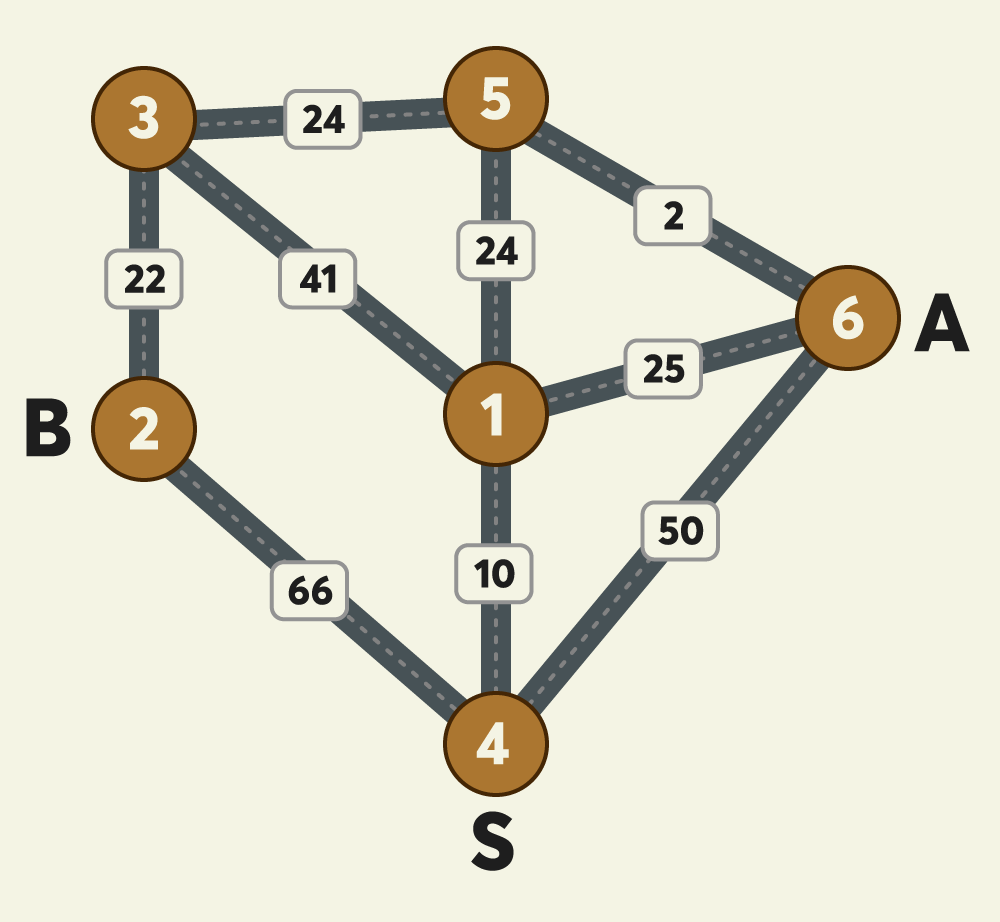
밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. "무지"는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. "무지"는 "어피치"와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을 지 계산해 보고 "어피치"에게 합승을 제안해 보려고 합니다.

접근

정리 하자면 S 지점에서 둘 다 출발해 어느 한 지점까지 합승 후 각각 A, B로 헤어질 때 가장 적은 택시요금을 구하여라 이다. 다익스트라를 써야한다!!

합승을 어느지점까지 해야할지 모르는 상황이다. 그렇다면, 모든 경우를 비교해줘야한다.
1 ~ n 각각의 지점까지 합승하는 경우를 다 비교해주면 된다.

i 지점 까지 합승 한 비용 = S 에서 i 지점까지 가는 최소 비용
i 지점에서 A 지점까지의 비용 = i 에서 A 지점까지 가는 최소 비용
i 지점에서 B 지점까지의 비용 = i 에서 B 지점까지 가는 최소 비용

다시 정리하면, S, A, B에 대해서 각각 1 ~ n 지점까지의 최소 비용들을 구하고 구한 비용의 합 들 중 가장 작은 것을 출력해주면 된다.

코드

//다익스트라
import java.util.*;
class Solution {
    static LinkedList<Node>[] doro;
    public int solution(int n, int s, int a, int b, int[][] fares) {
        int answer = 0;
        
        //도로 정보 정리 
        doro = new LinkedList[n+1];
        for(int i = 1; i <= n; i++) doro[i] = new LinkedList<>();
        for(int[] v : fares){
            doro[v[0]].add(new Node(v[1], v[2]));
            doro[v[1]].add(new Node(v[0], v[2]));
        }
        
        answer = getMinTaxiFare(s,a,b);
        return answer;
    }
    private static int getMinTaxiFare(int s, int a, int b){
        int maxV = 20000001;
        int doroLength = doro.length;
        
        //S, A, B 들의 1 ~ n 지점까지의 최소비용 배열을 만들어준다
        int[] arrS = new int[doroLength];
        int[] arrA = new int[doroLength];
        int[] arrB = new int[doroLength];
        Arrays.fill(arrS, maxV);
        Arrays.fill(arrA, maxV);
        Arrays.fill(arrB, maxV);
        dijkstra(s, arrS);
        dijkstra(a, arrA);
        dijkstra(b, arrB);
        
        int res = maxV;
        
        for(int i = 1 ; i < doroLength ; i++){
            //i지점까지 합승 후 각각 A, B로 나뉘는 경우
            res = Math.min(res, arrS[i] + arrA[i] + arrB[i]);
        }
        return res;
    }
    private static void dijkstra(int start, int[] arr){
        PriorityQueue<Node> mq = new PriorityQueue<>();
        
        mq.offer(new Node(start, 0));
        
        arr[start] = 0;
        
        while(!mq.isEmpty()){
            Node cur = mq.poll();
            int curN = cur.num;
            int curW = cur.weight;
            
            // 현재까지의 비용이 최단 비용의 값보다 크다면,
            // 그 경로는 사용할 필요가 없으니 continue;
            if(curW > arr[curN]) continue;
            
            for(int i = 0; i < doro[curN].size(); i++){
                if(arr[doro[curN].get(i).num] > curW + doro[curN].get(i).weight){
                    arr[doro[curN].get(i).num] = curW + doro[curN].get(i).weight;
                    mq.offer(new Node(doro[curN].get(i).num, 
                    curW+doro[curN].get(i).weight));
                }
            }
        }
    }
    static class Node implements Comparable<Node>{
        int num , weight;
        public Node(int num, int weight){
            this.num = num;
            this.weight = weight;
        }
        public int compareTo(Node o){
            return this.weight - o.weight;
        }
    }
}

다익스트라 방법 말고 하나가 더 생각이 날 것이다. 각 지점 사이의 최소비용을 구하는 것이므로 플로이드 와샬 알고리즘을 사용해도 된다.

코드

//플로이드 와샬
import java.util.*;
class Solution {
    public int solution(int n, int s, int a, int b, int[][] fares) {
        int answer = 20000001;
      
        int[][] arr = new int[n+1][n+1];
        for(int i = 1 ; i < n + 1; i++){
            Arrays.fill(arr[i], 20000001);
            arr[i][i] = 0;
        }
        
        //행렬 정보 생성
        for(int[] ae : fares){
            arr[ae[0]][ae[1]] = ae[2];
            arr[ae[1]][ae[0]] = ae[2];
        } 
       	//i,j,k 각각 다를 경우만 계산 하도록 if 조건을넣어줬다.
        for(int k = 1; k < n + 1; k++){
            for(int i = 1 ; i < n + 1; i++){
                if(k == i) continue;
                for(int j = 1; j < n + 1; j++){
                    if(i != j && k != j && arr[i][j] > arr[i][k] + arr[k][j])
                        arr[i][j] = arr[i][k] + arr[k][j];
                }
            }
        }
        
        for(int i = 1; i < n + 1 ;i++)
            answer = Math.min(answer, arr[s][i] + arr[i][a] + arr[i][b]);
        
        return answer;
    }  
}