
이 포스트는 FastCampus에 이 강의를 보고 포스팅되었습니다.
문제가 될 시 삭제될 예정입니다.
비선형?
아까 봤던 배열, 연결리스트, 스택, 큐와는 다른 구조입니다.
1:1에 관계가 아닌 1:n, n:m에 관계를 맺죠.
배우기 전에 노드에 대해 좀 짚고 가죠.
노드는 연결구조 또는 계층구조에서 데이터의 기본 단위를 뜻하는 단어입니다.
링크는 노드와 노드를 잇는 연결점입니다.
전에 선형구조에서 배웠던 연결리스트도 노드와 링크로 이루어져 있죠.
트리(Tree)

부모 노드가 있고, 양옆에 있는 노드를 자식 노드라고 부릅니다.
우리가 프로그래밍에서 많이 쓰는 트리는 이진 트리입니다.
- 이진 트리란, 자식 노드가 2개 이하인 트리입니다.
이진 트리에서도 대표적으로 쓰는 트리는 힙(Heap), 이진 검색 트리(BST)입니다.
힙(Heap)
힙은 완전 이진 트리입니다.
힙은 트리가 채워질 때 무조건 왼쪽 자식 노드부터 채워지죠.
이 트리가 꽉채워질때 이것을 완전 이진 트리라고 부른답니다.
힙에 특징은 다음과 같습니다.
- 루트 노드의 값이 가장 클 때 : Max Heap
- 루느 노드이 값이 가장 작을 때 : Min Heap
이때, 루트를 꺼낸다면, 트리가 다시 구현합니다.
- 서브트리 중, 가장 큰 값을 루트로 부른답니다.
이렇게 정렬하는 방법이 Heap Sort이에요.
- Max Heap으로 정렬하면 역순 정렬이 될 테고
- Min Heap으로 정렬하면 차순위 정렬이 된답니다
참고로, 힙은 중복 값이 들어갈 수 있습니다.
이진 검색 트리 ( Binary Search Tree )
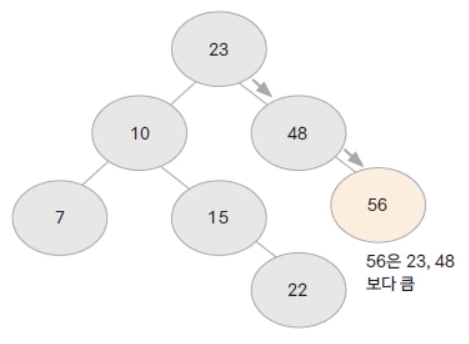
이진 검색 트리는 검색을 위해 만들어진 자료구조입니다.
그래서 힙과는 다르게 자료의 중복이 허용되지 않죠.
이 유일한 값을 우리는 키라고 부릅니다.
BST의 특징은 자식노드를 중심으로 왼쪽이 작은 값, 오른쪽이 큰 값을 가집니다.
위 사진에서 22를 찾을 때 어떻게 찾을까요?
- 23과 22를 비교 -> 작은 값 = 왼쪽으로
- 10과 22를 비교 -> 큰 값 = 오른쪽으로
- 15와 22를 비교 -> 큰 값 = 오른쪽으로
- 22와 22를 비교 -> 같은 값 = 연산 종료
왜 BST가 연산속도가 빠를까요?
- 완전 이진 트리로 생각해봅시다.
- 레벨이 n이고, 노드에 수는 2ⁿ- 1개이죠.
- 한번 연산하고 오면 비교해야 하는 범위가 절반이 되어 있죠.
- 그래서 찾아가는 데 걸리는 최대 시간이 log 2ⁿ시간입니다.
하지만, 항상 안정적으로 트리가 구성되지는 않습니다. 
위 사진처럼 구성될 수도 있죠. 이렇게 된 트리를 편향된 트리라고 합니다.
이렇게 편향된 트리에 BST를 쓴다면 연산 속도는 n이 될 것입니다.
그래서 위 같은 트리는 AVL 트리나 레드-블랙 트리를 사용합니다.
Inorder Traversal 탐색을 하게 된다면 자료가 정렬되어 출력됩니다.
Inorder Traversal : 부모를 기준으로 왼쪽 자식을 방문하고, 다시 루트를 방문하고 오른쪽 자식을 방문하는 식
아까 22 찾던 사진을 예로 들어봅시다.
- 23 -> 10 -> 7 -> 10 -> 15 -> 22 -> 23 -> 48 -> 56
- = 17 -> 10 -> 15 -> 22 -> 23 -> 48 -> 56 정렬됐죠?
그래프 ( Graph )
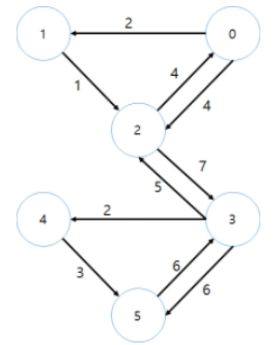
그래프도 범위가 굉장히 방대합니다.
- 네비게이션, 구글맵, 카카오맵 등이 그래프에 기반을 둬서 구현된 겁니다.
여기서는 노드를 vertex라고 하고, 링크를 edge라고 합니다.
V(vertex)를 서로 연결하는 E(edge)에 방향성이 있느냐 없느냐로 그래프에 종류를 구분할 수 있습니다.
그래프를 구현하는 방법은 크게 두 가지가 있습니다.
- 인접 행렬
- 인접 리스트
그래프를 탐색하는 알고리즘은 BFS, DFS가 있습니다.
이 내용은 너무 방대해서 알고리즘 쪽으로 가서 더 자세히 알아보겠습니다!
해싱 ( Hashing )
검색을 위한 자료구조입니다.
극장을 생각하시면 됩니다.
- 극장이 있고, 좌석표가 0 ~ 99번까지 있습니다.
- 이 극장이 사실 꽉 차지 않습니다. 그래서 표를 많이 팔았답니다.
- 표를 300장을 팔았답니다. 만약 55번 고객이 오면 어디에 앉힐까요?
- 55 % 100을 해서 나온 나머지 55번에 가서 앉히면 됩니다.
- 123번이 왔을 때는? 123 % 100를 해서 나온 23번에 앉히면 됩니다.
- 표 번호 % 좌석 수에서 % 가 해시함수가 되는 겁니다.
키는 유일하고, 이에 대한 value를 쌍으로 저장합니다.
사전이랑 비슷한 개념이라고 보시면 됩니다.
- 김치의 뜻을 찾을 때 그 뜻들은 value가 되고 김치는 키가 되는겁니다.
그래서 해싱을 다른 말로 딕셔너리라고 합니다.
파이썬에서는 딕셔너리를 제공합니다.
그런데요, 만약 위 예에서 223번이 오면 어떻게 될까요?
- 223 % 100 = 23번 근데 이미 앉고 있죠?
- 이럴 때에도 여러 가지 해결 방법이 있습니다.
- 대표적인 건 "옆에 앉으세요~"하면서 키를 1번 increase 시키는 겁니다.
이 해시 알고리즘을 쓰는 가장 큰 이유는 검색 속도가 산술적으로 가능하기 때문입니다.
지금까지에 검색 자료구조들은 배열 이외에는 산술적으로 시간이 들어가는 경우가 흔하지 않습니다.
해싱 같은 경우, 검색에 들어가는 속도가 굉장히 빠릅니다.
해싱을 효율적으로 관리할 수 있는 것으로 나온 것이 해시테이블입니다.
해시테이블에 들어가기 전에 중요한 점
가장 먼저는 해시 함수를 어떻게 만드느냐가 중요합니다.
실제로 키값은 여러 가지 종류가 있어요. 이 키값에 대한 고민을 많이 해보시고 해시함수를 보완해놓으시는 게 중요합니다.
그렇다고 충돌이 발생하지 않는다는 게 아니에요. 상황에 따라서 쓰라는 거죠.
해시테이블을 하나에 줄만 사용한다고 가정해볼게요.
그러면 오히려 데이터 검색할 때나 꺼내올 때 시간이 더 걸릴 수 있어요.
위에처럼 인덱스를 1개 1개 늘려가면서 찾으면 그만큼 시간이 소모되니까요.
이걸 오버헤드라고 해요.
자바에서는 오버헤드가 일어나지 않게끔 해시테이블이 76% 차면 다시 재구성하도록 구현되어 있어요.
해시테이블
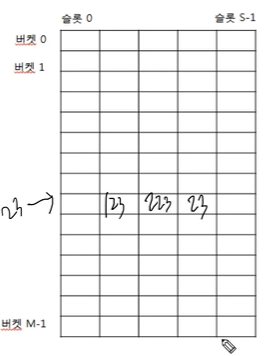
2차원 배열처럼 생겼죠?
말 그대로, 23번에 value들이 이웃이 되는 거에요.
하지만 이러면 안 쓰는 공간이 많게 돼요.
그래서 버킷과 슬롯이 많이 있을수록 오버헤드가 일어날 수 있어요.
그래서 대안으로 나온 메모리가 있어요.
체이닝

연결 리스트를 활용한 방식이에요.
key에 해당하는 인덱스에 value를 연결하는 방식이에요.
그러면 배열처럼 안 쓰는 공간이 발생한다든가 슬롯이 부족하다던가 하는 문제는 없을 거에요.
하지만, 그만큼 구현이 복잡해요.
아무래도 배열보다는 연결리스트가 구현하기 어렵죠.
자료구조 종류를 우리가 직접 짜야 됨?
우리가 직접 자료구조를 짜야 할 때도 있지만, 자바에서는 거의 짤 필요가 없습니다.
왜냐면 JDK(Java Developer Kit)가 자료구조를 많이 구현해놨기 때문이죠.

참고로 C++에서도 STL이라는 라이브러리에서 많이 구현되어 있습니다.
BST는 TreeSet, TreeMap으로 구현되어 있고, 해싱은 HashMap, Properties로 구현되어 있습니다.
진짜 존나 감사합니다 ㅠㅠ
마치며
네. 종류에 대한 설명은 이 정도면 될 거 같네요.
이제 한번 앞서 소개한 것들을 구현해볼 거에요.
다음 포스팅 때 말하겠지만 모든 코드는 깃 허브에 올라와 있어요.
Velog 코드블록 기능으로 쓰기도 할 거지만, 될 수 있으면 깃헙에서 코드를 보시고 포스팅 글을 보시면 될 거같아요.
수고하셨습니다.
