Codility_FrogJmp

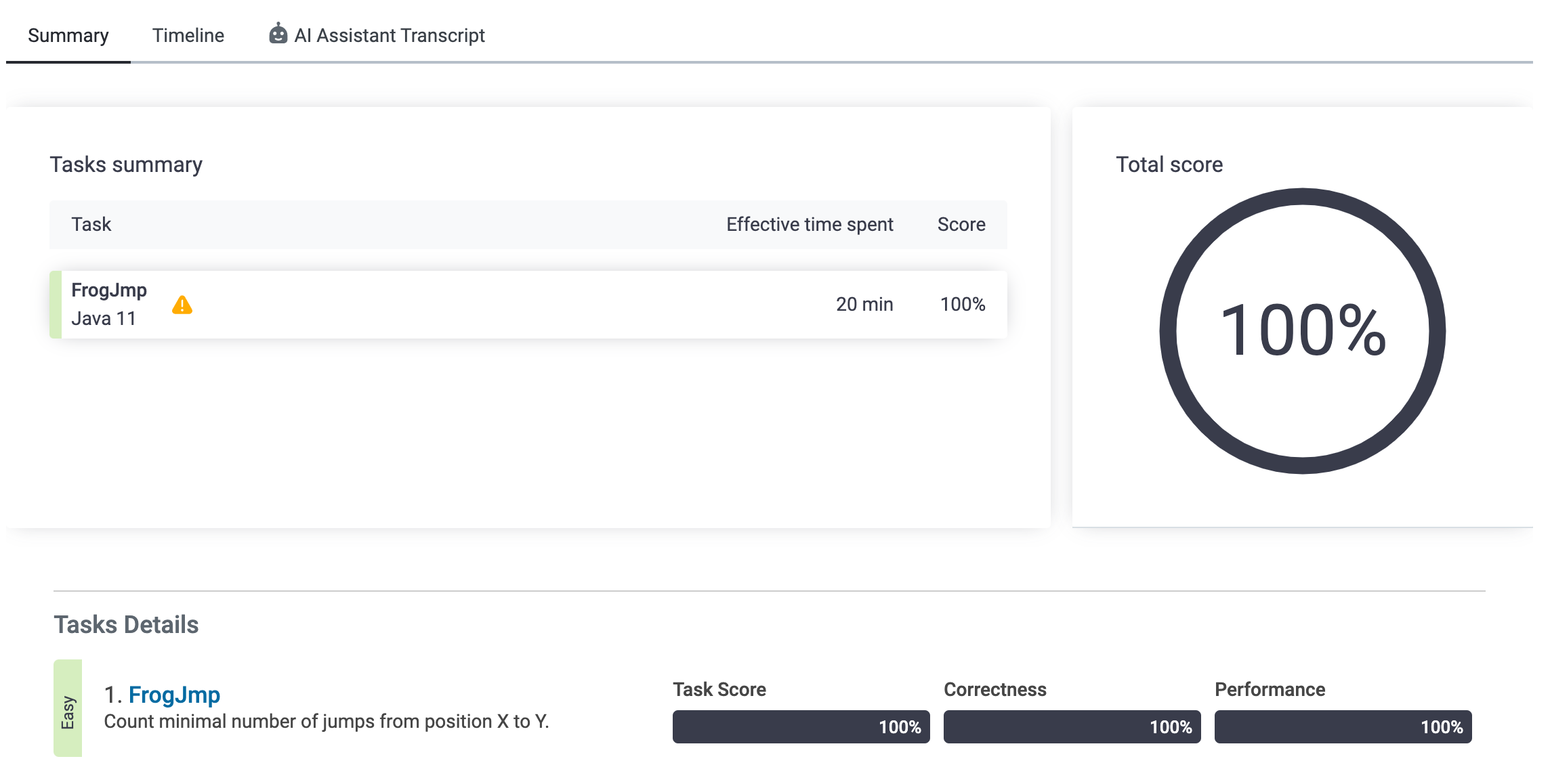
3-1. FrogJmp
A small frog wants to get to the other side of the road. The frog is currently located at position X and wants to get to a position greater than or equal to Y. The small frog always jumps a fixed distance, D.

Count the minimal number of jumps that the small frog must perform to reach its target.

Write a function:

class Solution { public int solution(int X, int Y, int D); }

that, given three integers X, Y and D, returns the minimal number of jumps from position X to a position equal to or greater than Y.

For example, given:

X = 10
Y = 85
D = 30
the function should return 3, because the frog will be positioned as follows:

after the first jump, at position 10 + 30 = 40
after the second jump, at position 10 + 30 + 30 = 70
after the third jump, at position 10 + 30 + 30 + 30 = 100
Write an efficient algorithm for the following assumptions:

X, Y and D are integers within the range [1..1,000,000,000];
X ≤ Y.

이 문제는 개구리가 위치 X에서 위치 Y로 고정된 점프 거리 D를 사용하여 이동할 때 필요한 최소 점프 수를 계산하면 됩니다.

문제풀이

class Solution {
    public int solution(int X, int Y, int D) {
        // Implement your solution here
        int jumpDistance = (Y - X);
        int Ne = jumpDistance % D;
        if(Ne != 0){
            return ((jumpDistance / D) + 1);
        }else{
            return (jumpDistance / D);
        }
    }
}

jumpDistance에서 미리 점프해야 하는 거리를 계산하고
나머지 값이 있을 겅우에는 +1
나머지 값이 없을 경우에는 바로 나눈값을 리턴해주는 방식으로 문제를 풀었습니다.

해당 방식으로도 풀이가 가능하지만 검색해보니 Math.ceil함수를 사용하면 더 간단하게 코드를 구현할 수 있습니다.

해당 함수를 사용한 문제풀이->

class Solution {
    public int solution(int X, int Y, int D) {
        int distance = Y - X;
        return (int) Math.ceil((double) distance / D);
    }
}

Math.ceil 함수는 소수점을 올림하여 정수로 변환합니다.
해당 함수를 사용하여 총 거리를 점프 거리 D로 나눈 값을 올림하여 최소 점프 수를 계산합니다.
더 깔끔하게 작성이 가능합니다.

문제 풀어보기 ->
https://app.codility.com/programmers/lessons/3-time_complexity/frog_jmp/