Codility_MinPerimeterRectangle

10-2. MinPerimeterRectangle

An integer N is given, representing the area of some rectangle.

The area of a rectangle whose sides are of length A and B is A B, and the perimeter is 2 (A + B).

The goal is to find the minimal perimeter of any rectangle whose area equals N. The sides of this rectangle should be only integers.

For example, given integer N = 30, rectangles of area 30 are:

(1, 30), with a perimeter of 62,
(2, 15), with a perimeter of 34,
(3, 10), with a perimeter of 26,
(5, 6), with a perimeter of 22.
Write a function:

class Solution { public int solution(int N); }

that, given an integer N, returns the minimal perimeter of any rectangle whose area is exactly equal to N.

For example, given an integer N = 30, the function should return 22, as explained above.

Write an efficient algorithm for the following assumptions:

N is an integer within the range [1..1,000,000,000].

정수 N이 주어졌을 때, 이는 어떤 직사각형의 넓이를 나타냅니다.

한 변의 길이가 A와 B인 직사각형의 넓이는 A B이고, 둘레는 2 (A + B)입니다.

목표는 넓이가 N인 직사각형의 둘레 중 최소값을 찾는 것입니다. 이 직사각형의 변의 길이는 모두 정수여야 합니다.

예를 들어, 주어진 정수 N = 30일 때, 넓이가 30인 직사각형은 다음과 같습니다:

(1, 30), 둘레는 62, (2, 15), 둘레는 34, (3, 10), 둘레는 26, (5, 6), 둘레는 22.

다음과 같은 함수를 작성하세요:

class Solution { 
    public int solution(int N); 
}

이 함수는 정수 N이 주어졌을 때, 넓이가 정확히 N인 직사각형의 최소 둘레를 반환해야 합니다.

예를 들어, 정수 N = 30이 주어졌을 때, 함수는 위에서 설명한 대로 22를 반환해야 합니다.

다음 가정을 위한 효율적인 알고리즘을 작성하세요:

N은 [1…1,000,000,000] 범위 내의 정수입니다.

문제풀이

import java.util.*;

class Solution {
    public int solution(int N) {
        int minPerimeter = Integer.MAX_VALUE;
        for (int i = 1; i * i <= N; i++) {
            if (N % i == 0) {
                int A = i;
                int B = N / i;
                int perimeter = 2 * (A + B);
                minPerimeter = Math.min(minPerimeter, perimeter);
            }
        }
        return minPerimeter;
    }
}

이전문제인 CountFactors와 유사하게 반복문에서 i * i <= N의 범위 지정을 통해 반복문의 반복횟수를 줄여 시간을 단축하였습니다. 왜냐하면 주어진 정수가 직사각형의 넓이이기 때문에 해당 정수의 약수가 한변의 길이 A와 B가 될 수있습니다.

하여 약수에 해당하는 값만 거른뒤 2*(A+B) 한변의길이A와B를 더하고 2를 곱한값 => 둘레를 계산하여 perimeter에 저장하고 이를 비교하여 최소값으로 업데이트합니다.

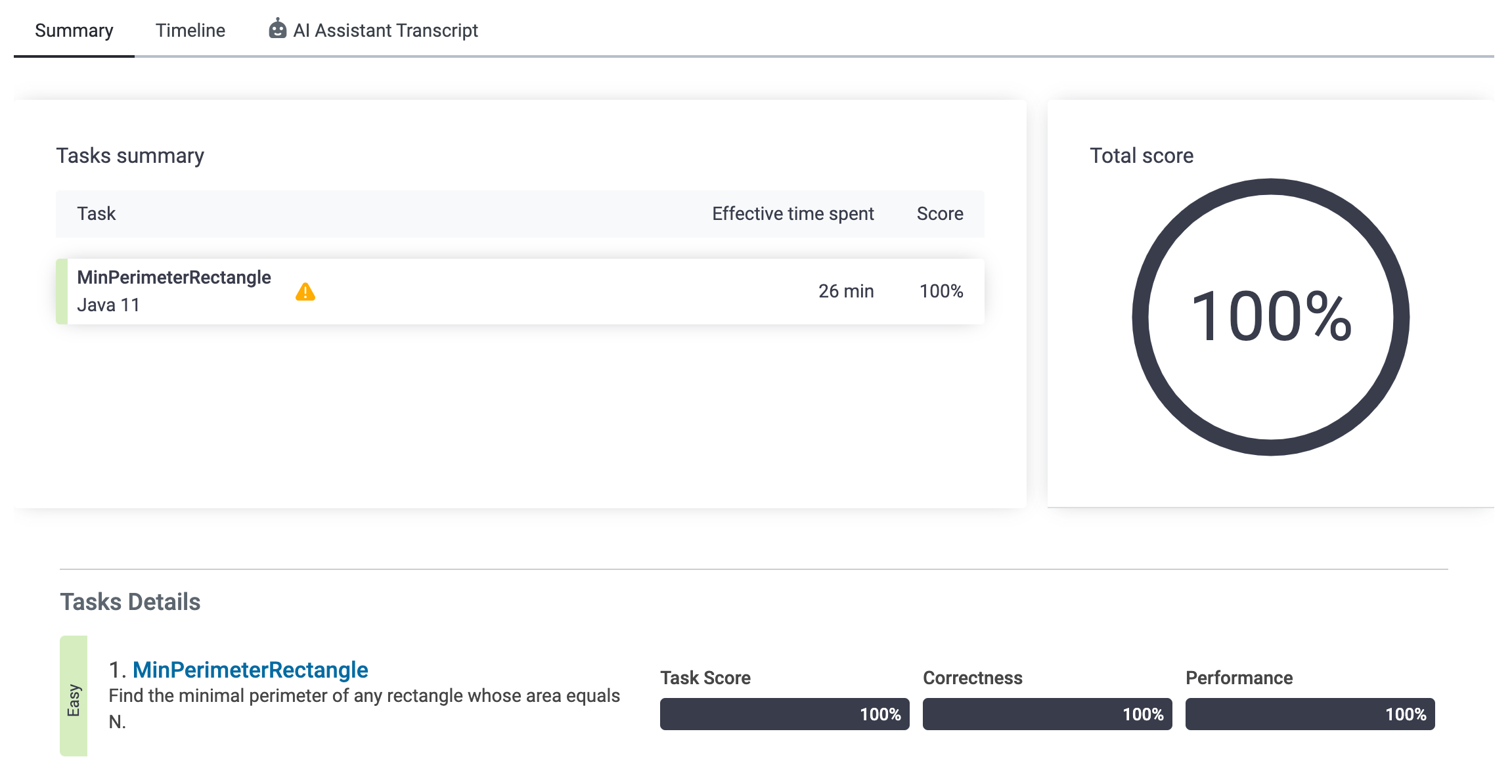
제출결과

문제풀어보기 -> https://app.codility.com/programmers/lessons/10-prime_and_composite_numbers/min_perimeter_rectangle/