Codility_TapeEquilibrium

3-3. TapeEquilibrium
A non-empty array A consisting of N integers is given. Array A represents numbers on a tape.

Any integer P, such that 0 < P < N, splits this tape into two non-empty parts: A[0], A[1], ..., A[P − 1] and A[P], A[P + 1], ..., A[N − 1].

The difference between the two parts is the value of: |(A[0] + A[1] + ... + A[P − 1]) − (A[P] + A[P + 1] + ... + A[N − 1])|

In other words, it is the absolute difference between the sum of the first part and the sum of the second part.

For example, consider array A such that:

A[0] = 3
A[1] = 1
A[2] = 2
A[3] = 4
A[4] = 3
We can split this tape in four places:

P = 1, difference = |3 − 10| = 7
P = 2, difference = |4 − 9| = 5
P = 3, difference = |6 − 7| = 1
P = 4, difference = |10 − 3| = 7
Write a function:

class Solution { public int solution(int[] A); }

that, given a non-empty array A of N integers, returns the minimal difference that can be achieved.

For example, given:

A[0] = 3
A[1] = 1
A[2] = 2
A[3] = 4
A[4] = 3
the function should return 1, as explained above.

Write an efficient algorithm for the following assumptions:

N is an integer within the range [2..100,000];
each element of array A is an integer within the range [−1,000..1,000].

비어 있지 않은 N개의 정수로 구성된 배열 A가 주어집니다. 배열 A는 테이프의 숫자를 나타냅니다.

[3][1][2][4][3]이 주어질 경우

[3] - [1][2][4][3]
[3][1] - [2][4][3][3][1][2] - [4][3]
[3][1][2][4] - [3]
위 4가지 경우 중 최소 차이를 반환하면 됩니다.

문제풀이

// you can also use imports, for example:
import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    public int solution(int[] A) {
        int totalSum = 0;
        for (int num : A) {
            totalSum += num;
        }

        int minDifference = Integer.MAX_VALUE;
        int leftSum = 0;

        for (int i = 0; i < A.length - 1; i++) {
            leftSum += A[i];
            int rightSum = totalSum - leftSum;
            int difference = Math.abs(leftSum - rightSum);
            minDifference = Math.min(minDifference, difference);
        }

        return minDifference;
    }
}

for문을 통해 우선 전체 더한 값을 구하고
이후 A.length의 1을 뺀만큼 for문을 실행하여
leftSum을 저장하면서 전체 값에서 뺀값을 rightSum에 저장해 주었습니다.

여기서 Integer.MAX_VALUE는 java에서 사용할 수 있는 가장 큰 정수 값으로 초기값으로 설정하면 비교할 때 바로 이보다 작은 값으로 업데이트가 가능합니다.

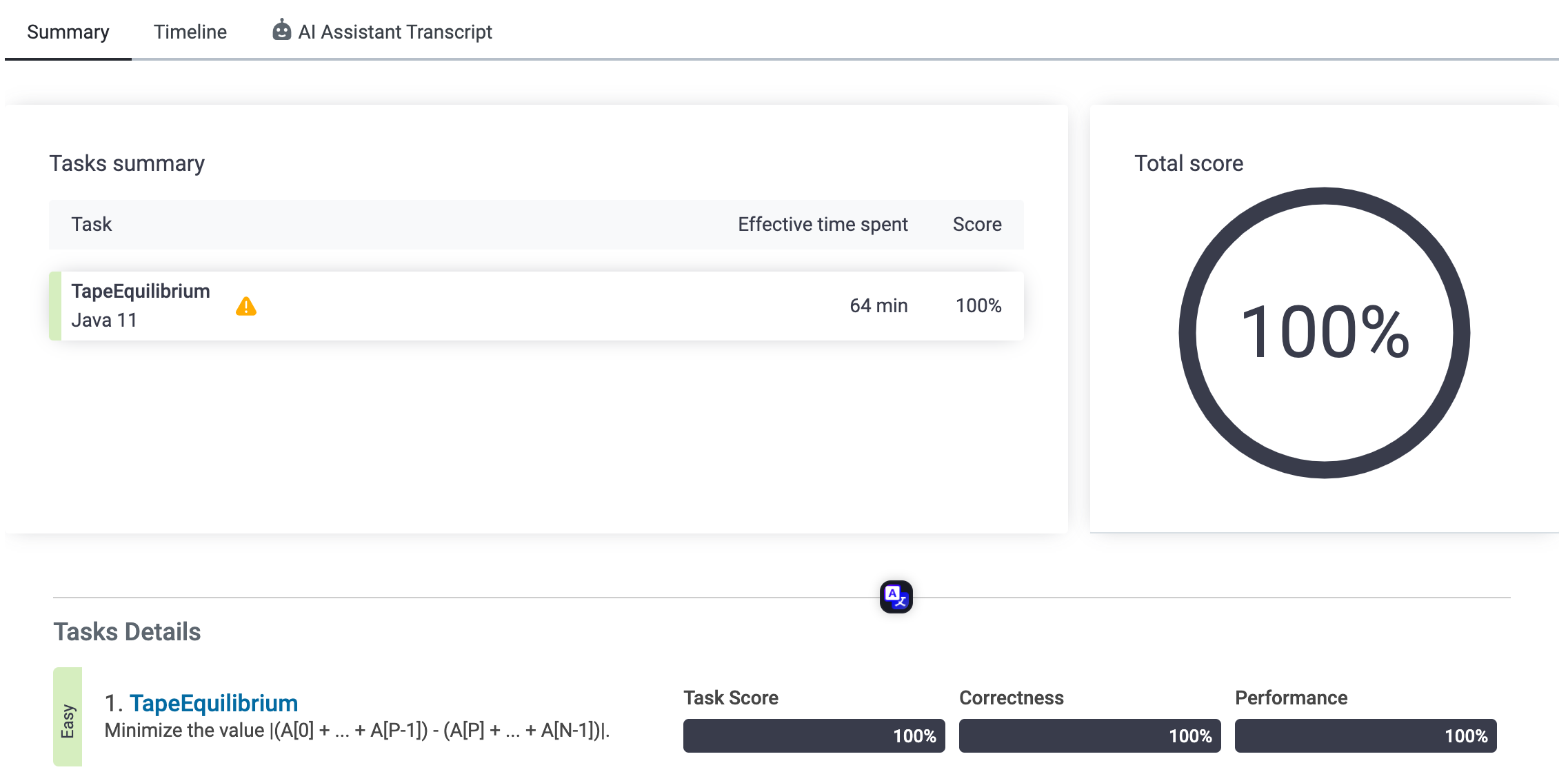
점수체크

문제풀어보기 -> https://app.codility.com/programmers/lessons/3-time_complexity/tape_equilibrium/