앞서 이진 탐색 트리에 대해 살펴봤듯이, 이진 탐색 트리는 한쪽으로 쏠릴 경우 시간 복잡도가 O(n) 으로 상승하는 것을 알 수 있었다. 이러한 문제를 보완하고자 나온 트리 중 하나가 AVL 트리다.
🍭 AVL 트리란?
AVL 트리란 자가 균형 이진 탐색 트리 중 하나로, 각 노드의 서브트리 높이 차이가 최대 1을 유지하도록 한다.
여기서 서브트리의 높이 차이를 균형 계수(Balance Factor, BF)라 한다. 삽입, 삭제 연산을 수행할 때 마다 트리의 균형 계수를 체크하여 균형 계수가 1보다 커질 때 Rotation을 통해 균형을 유지한다.
균형 계수 (Balance Factor, BF)
AVL트리는 균형이 무너졌는지에 대해 판단할 때 Balance Factor라는 것을 활용한다.
BF(K) = K의 왼쪽 서브트리의 높이 - K의 오른쪽 서브트리의 높이
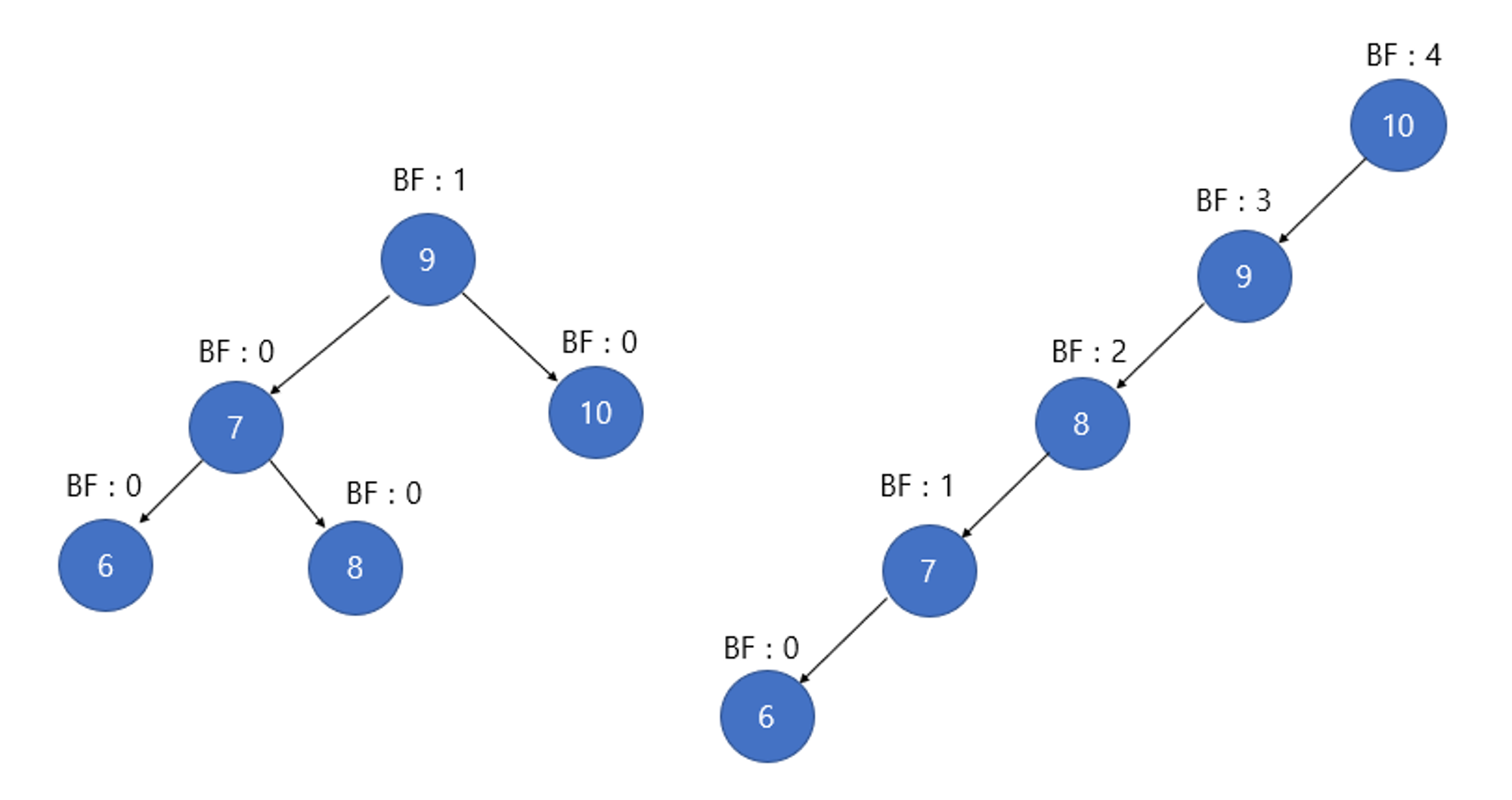
AVL트리는 모든 노드의 BF가 -1, 0, 1 중 하나여야 한다. 만약 이를 벗어나면 균형이 깨졌다는 것을 의미하고, 이때 회전이 필요하다.
Left and Right Rotatation
- Left Rotation
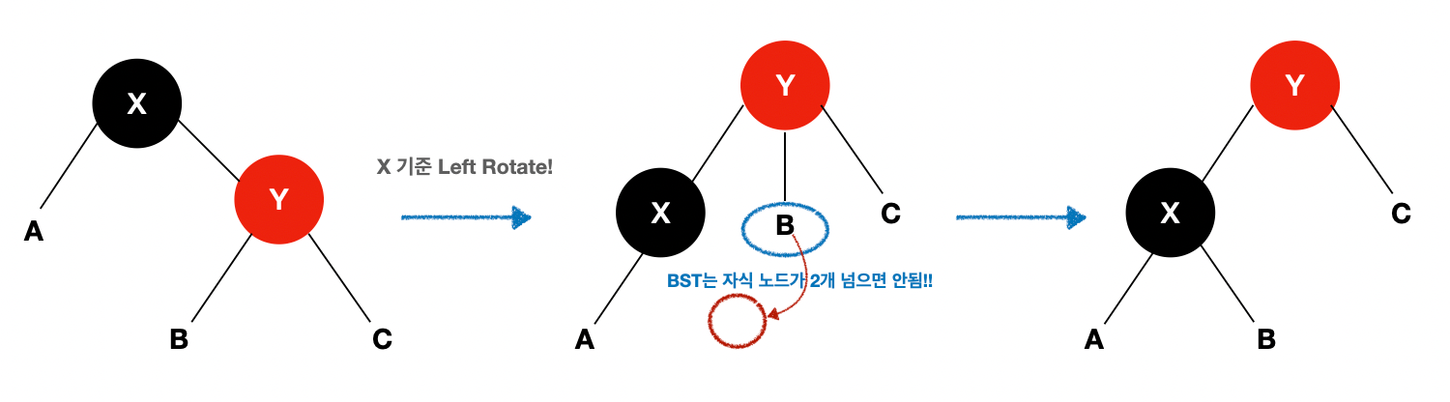
- Right Rotation
- 위와 반대로 하면 된다!
AVL 트리의 특징
- 이진 검색 트리(Binary Search Tree)
- 모든 노드의 두 하위 트리의 높이는 최대 1까지 차이가 난다.
- 트리의 모든 노드는 노드에서 리프 노드까지의 가장 긴 경로 길이인 높이 값을 갖는다.
- 루트 노드는 높이 0에 위치한다.
- 노드의 균형 계수는 항상 -1, 0, 1이다.
🤖 동작 과정
AVL트리는 LL, LR, RL, RR 4가지의 균형이 무너진 경우가 존재한다. 각각 해결법을 알아보자.
1. LL(Left Left) Case
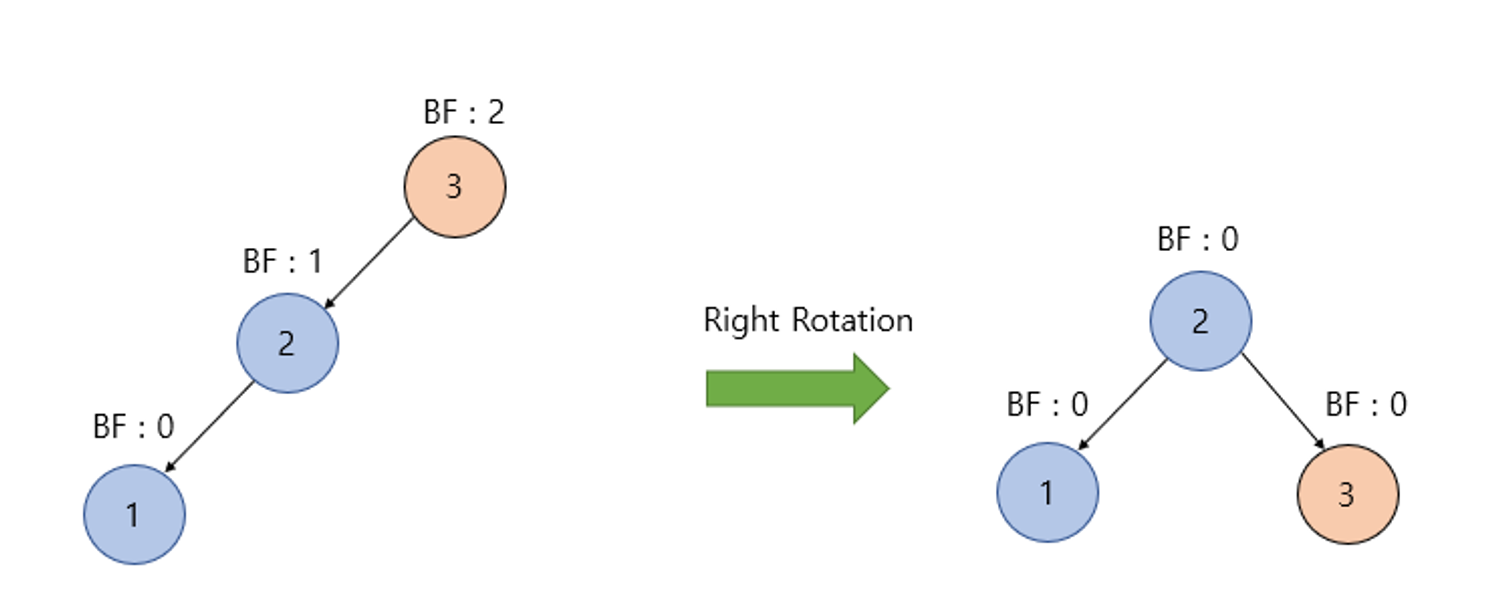
위 그림처럼 BF가 -1~1을 벗어난 노드를 기준으로 왼쪽, 왼쪽 노드가 존재한다면 LL Case이다.
이때 해당 노드를 기준으로 우회전을 적용하면 불균형이 해소된다.
2. RR(Right Right) Case
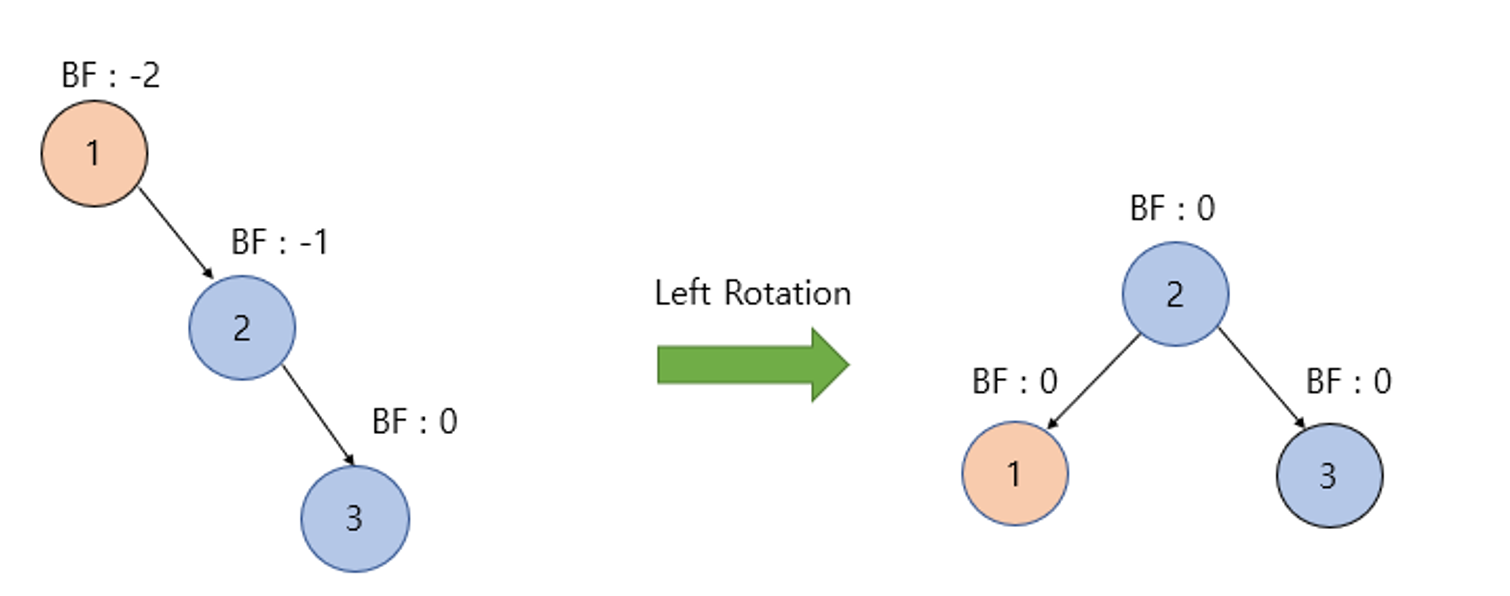
위 그림처럼 BF가 -1~1을 벗어난 노드를 기준으로 오른쪽, 오른쪽 노드가 존재한다면 RR Case이다.
이때 해당 노드를 기준으로 좌회전을 적용하면 불균형이 해소된다.
3. LR(Left Right) Case
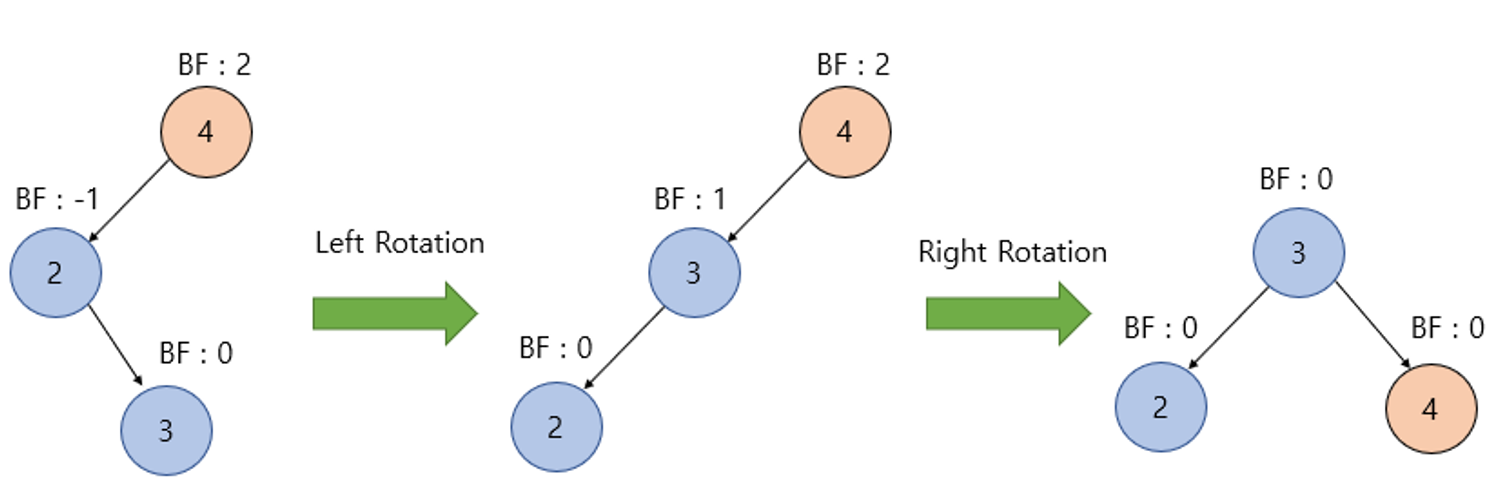
위 그림처럼 BF가 -1~1을 벗어난 노드를 기준으로 왼쪽, 오른쪽 노드가 존재한다면 LR Case이다.
이때 먼저 BF에 이상이 있는 노드(값이 4인노드)의 왼쪽 자식노드(값이 2인 노드)를 기준으로 좌회전을 진행한다.
이후 BF에 이상이 있는 노드(값이 4인 노드)를 기준으로 우회전을 진행하면 불균형이 해소된다.
4. RL(Right Left) Case
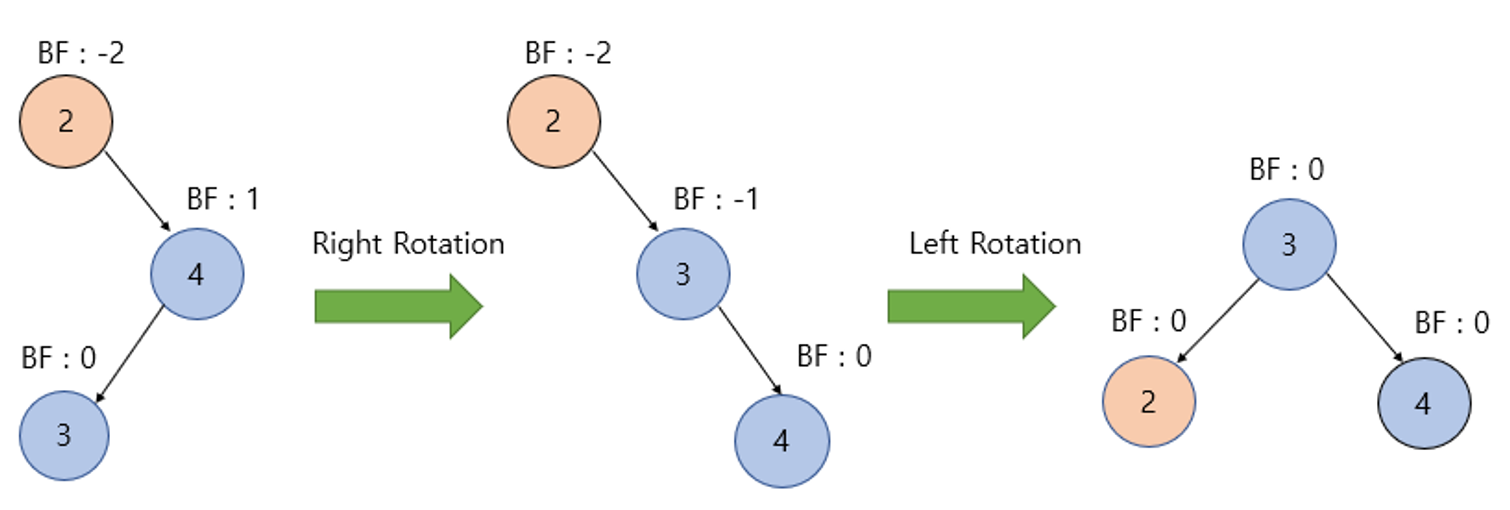
위 그림처럼 BF가 -1~1을 벗어난 노드를 기준으로 오른쪽(Right), 왼쪽(Left) 노드가 존재한다면 RL Case이다.
이때 먼저 BF에 이상이 있는 노드(값이 4인노드)의 오른쪽 자식노드(값이 4인 노드)를 기준으로 우회전을 진행한다.
이후 BF에 이상이 있는 노드(값이 4인 노드)를 기준으로 좌회전을 진행하면 불균형이 해소된다.
📚 참고 자료
