[BOJ 2565] 전깃줄 - java

BOJ 2565 : 전깃줄

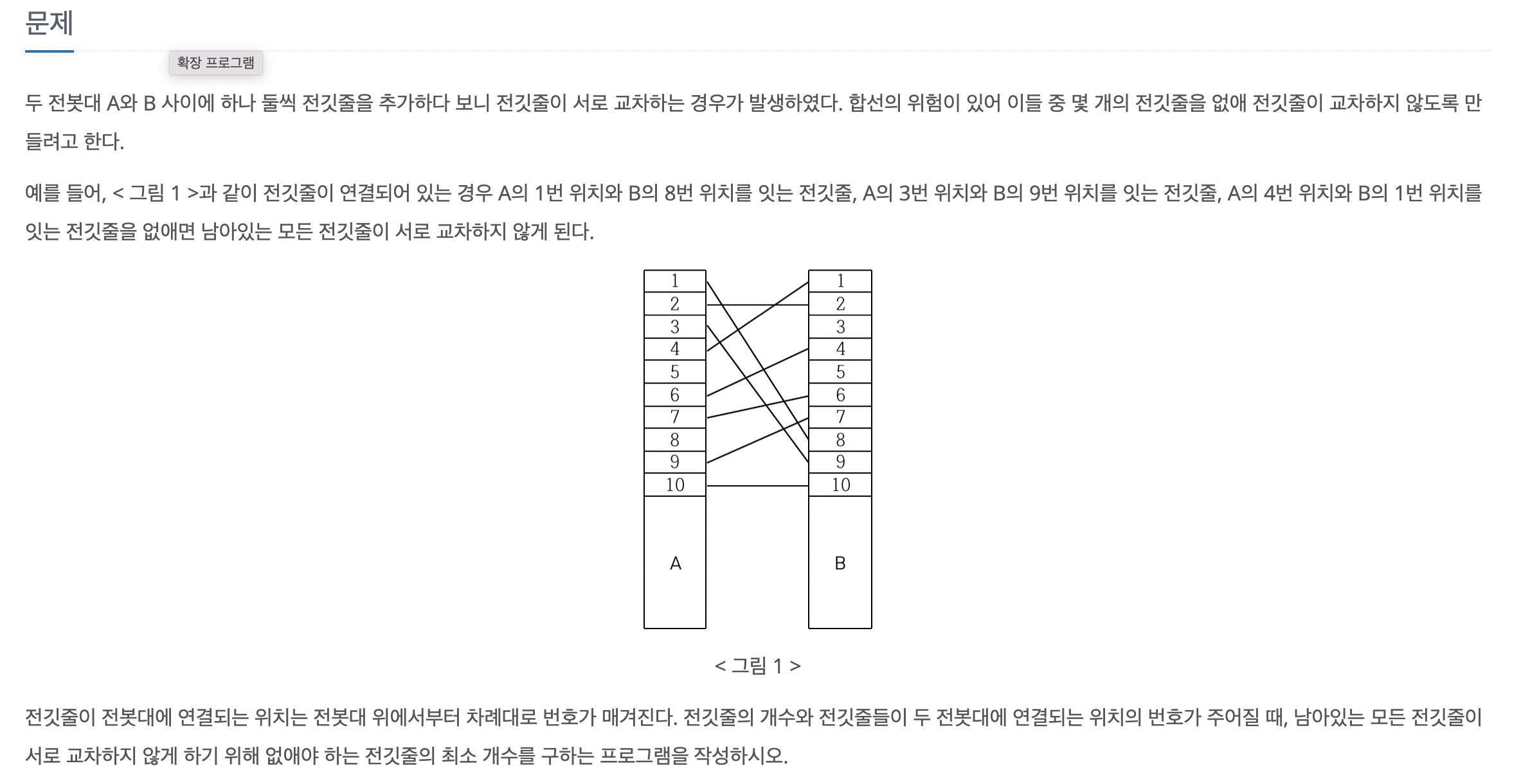
구해야 할 것 👉 없애야 하는 전깃줄의 최소 개수

근데 반대로 생각하면 설치 가능한 전깃줄의 최대 개수를 구하면 된다!

풀이

1. 입력

wire[i][0] : A 전봇대에서의 위치

wire[i][1]: B 전봇대에서의 위치

그리고 wire[i][0]을 기준으로 오름차순 정렬한다.

2. DP 테이블 정의

dp[i] : i 번째 전깃줄까지 고려했을 때 설치 가능 개수

3. 점화식 찾기

for (int j = 0; j < i; j++) {
    if (wire[i][1] > wire[j][1]) dp[i] = Math.max(dp[i], dp[j] + 1);
}

dp[i]를 정의하기 위해서는, i 보다 앞서는 j들에 대해 겹치는지의 여부를 확인하고 dp 값을 갱신해주면 된다.

4. 초기값

dp[i] = 1
👉 i 번째에서 최소한 i 번째 전깃줄은 설치할 수 있다

전체 코드

public class BOJ_2565 {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        int n = Integer.parseInt(br.readLine());
        int[][] wire = new int[n][2];
        for (int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine());
            wire[i][0] = Integer.parseInt(st.nextToken());
            wire[i][1] = Integer.parseInt(st.nextToken());
        }

        Arrays.sort(wire, (o1, o2) -> o1[0] - o2[0]);

        int max = -1;
        int[] dp = new int[n];
        for (int i = 0; i < n; i++) {
            dp[i] = 1;

            for (int j = 0; j < i; j++) {
                if (wire[i][1] > wire[j][1]) dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            max = Math.max(max, dp[i]);
        }
        System.out.println(n - max);
    }
}