이진 탐색 트리 (Binary Search Tree, BST) + 동작 과정

🌵 이진 탐색 트리란?

이진 탐색 트리란, 정렬된 이진트리로써 다음과 같은 속성을 갖고 있다.

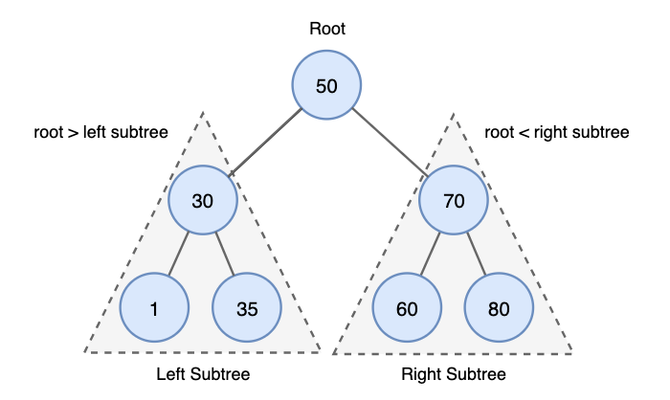
1. 모든 노드의 키는 유일하다.
2. 왼쪽 서브트리의 모든 키는 루트 노드의 키보다 작다
3. 오른쪽 서브트리의 모든 키는 루트 노드의 키보다 크다
4. 서브트리도 이진탐색트리이다.

👉 이를 통해 효율적인 검색이 가능하다!!

🤖 동작 방식

1. 탐색

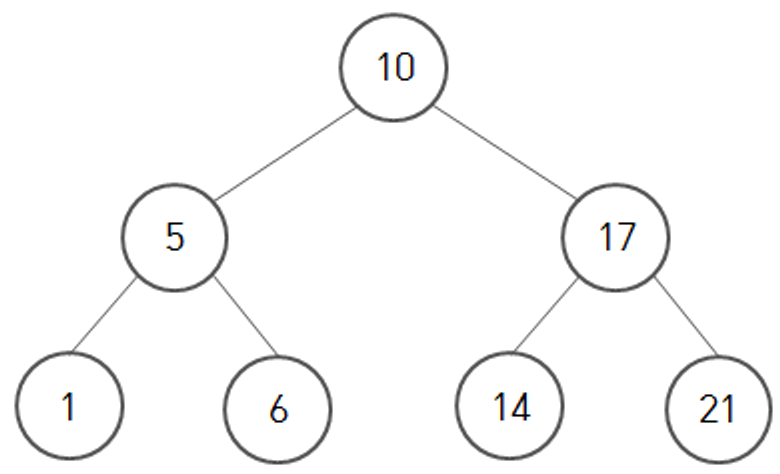
위의 트리에서 14라는 노드를 찾아보자!

루트 노드인 10과 비교했을 때, 14가 더 크므로 오른쪽 서브트리로 이동한다.

오른쪽 서브 트리의 루트 노드인 17과 비교했을 때 작으므로 왼쪽 서브트리로 이동한다.

14 발견!

2. 삽입

위의 트리에 12라는 노드를 삽입해보자!

루트 노드인 10보다 크므로, 왼쪽 서브트리로 이동 → 서브트리의 노드인 17보다 작으므로 왼쪽 서브트리로 이동 → 서브트리의 노드인 14보다 작으므로 왼쪽에 배치!

3. 삭제

삭제는 3가지 케이스로 나눌 수 있다고 한다.

• 단말 노드인 경우
  • 해당 노드만 지우면 된다.
• 왼쪽이나 오른쪽 서브 트리 중 하나만 가지고 있는 경우
  • 삭제되는 노드의 자식 노드와 부모 노드를 연결한다.
• 삭제할 노드의 자식 노드가 두 개 있는 경우

  • 지우려는 노드의 왼쪽 서브트리에서 가장 큰 값 or 오른쪽 서브트리에서 가장 작은 값으로 메꾼다.

    👉 삭제되는 노드와 가장 값이 비슷한 노드를 정해야 다른 노드들을 이동시키지 않아도 트리가 유지된다.

🦖 한계

n개의 노드를 갖는 BST 경우, 평균적인 시간 복잡도는 트리의 높이인 O(logn) 이다.

하지만 트리간 한 쪽으로 치우치는 최악의 경우에는 트리의 높이가 n이 되며, 시간 복잡도는 O(n) 이 된다.

이를 해결하고자, 트리의 균형을 유지하는 기법들이 많이 개발되었다.

👉 AVL 트리, 레드-블랙 트리, B-트리