정의

연결 리스트는 노드(Node)들이 포인터를 통해 연결된 선형 자료구조다. 각 노드는 데이터와 다음 노드를 가리키는 포인터(또는 참조)로 구성된다.

현실에 비유하자면

보물찾기 게임의 단서들

• 각 장소에서 "다음 단서는 도서관에 있다"는 메모를 남김
• 특정 단서를 찾으려면 처음부터 순서대로 따라가야 한다 - O(n) 접근
• 중간에 새로운 단서를 추가하는 것은 쉽다 - O(1) 삽입
• 한 장소를 건너뛰고 싶으면 이전 장소의 메모만 바꾸면 된다

지하철 노선

• 각 역에서 "다음 역은 ○○역"이라는 안내가 있다
• 특정 역에 가려면 순서대로 지나가야 한다
• 새로운 역을 중간에 추가하는 것은 연결만 바꾸면 쉽다
• 하지만 "3번째 역이 어디지?"라고 물어보면 처음부터 세어야 한다

회사의 보고 체계

• 직원 A → 팀장 B → 부장 C → 이사 D 순으로 연결
• 새로운 중간 관리자를 추가하기 쉽다 (연결만 변경)
• 하지만 "5단계 위 상사가 누구지?"를 알려면 하나씩 올라가야 한다

구조

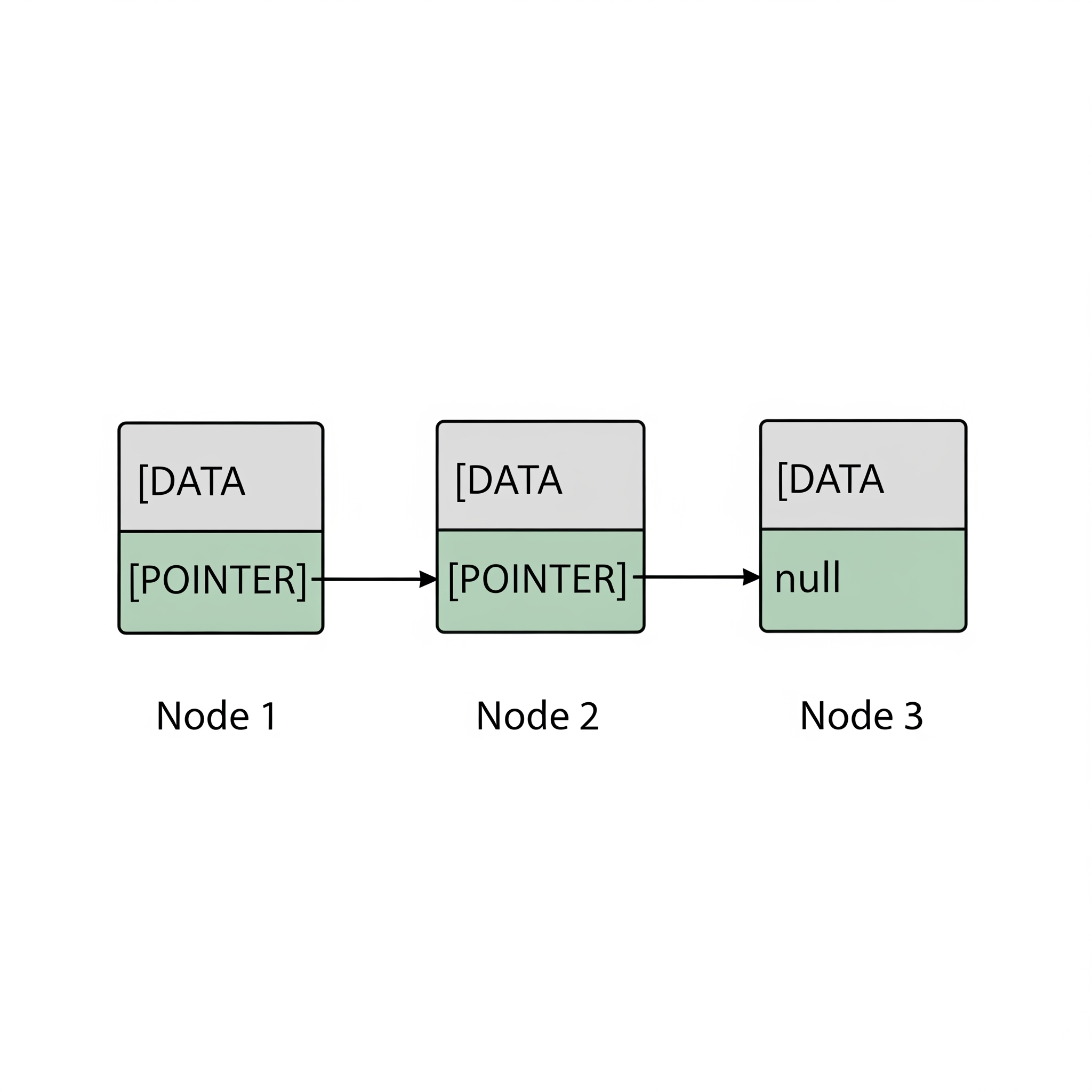
연결 리스트의 종류

단일 연결 리스트 (Singly Linked List)

각 노드가 다음 노드만을 가리키는 구조다.

이중 연결 리스트 (Doubly Linked List)

각 노드가 이전 노드와 다음 노드를 모두 가리키는 구조다.

원형 연결 리스트 (Circular Linked List)

마지막 노드가 첫 번째 노드를 가리켜 순환하는 구조다.

시간 복잡도

연산	시간 복잡도	설명
접근 (Access)	O(n)	처음부터 순차적으로 탐색
검색 (Search)	O(n)	선형 검색 필요
삽입 (Insert)	O(1)	위치를 알고 있다면
삭제 (Delete)	O(1)	위치를 알고 있다면

공간 복잡도

• O(n): n개의 노드와 각 노드마다 추가 포인터 저장 공간

JavaScript/TypeScript 구현

노드 클래스 정의

class ListNode<T> {
  data: T;
  next: ListNode<T> | null;

  constructor(data: T) {
    this.data = data;
    this.next = null;
  }
}

단일 연결 리스트 구현

class SinglyLinkedList<T> {
  private head: ListNode<T> | null;
  private size: number;

  constructor() {
    this.head = null;
    this.size = 0;
  }

  // 리스트 맨 앞에 삽입
  prepend(data: T): void {
    const newNode = new ListNode(data);
    newNode.next = this.head;
    this.head = newNode;
    this.size++;
  }

  // 리스트 맨 뒤에 삽입
  append(data: T): void {
    const newNode = new ListNode(data);
    
    if (!this.head) {
      this.head = newNode;
    } else {
      let current = this.head;
      while (current.next) {
        current = current.next;
      }
      current.next = newNode;
    }
    this.size++;
  }

  // 특정 인덱스에 삽입
  insertAt(index: number, data: T): void {
    if (index < 0 || index > this.size) {
      throw new Error('Index out of bounds');
    }

    if (index === 0) {
      this.prepend(data);
      return;
    }

    const newNode = new ListNode(data);
    let current = this.head;
    
    for (let i = 0; i < index - 1; i++) {
      current = current.next;
    }
    
    newNode.next = current.next;
    current.next = newNode;
    this.size++;
  }

  // 데이터로 검색
  find(data: T): ListNode<T> | null {
    let current = this.head;
    while (current) {
      if (current.data === data) {
        return current;
      }
      current = current.next;
    }
    return null;
  }

  // 인덱스로 삭제
  removeAt(index: number): T | null {
    if (index < 0 || index >= this.size || !this.head) {
      return null;
    }

    if (index === 0) {
      const data = this.head.data;
      this.head = this.head.next;
      this.size--;
      return data;
    }

    let current = this.head;
    for (let i = 0; i < index - 1; i++) {
      current = current.next;
    }

    const nodeToRemove = current.next;
    const data = nodeToRemove.data;
    current.next = nodeToRemove.next;
    this.size--;
    
    return data;
  }

  // 배열로 변환
  toArray(): T[] {
    const result: T[] = [];
    let current = this.head;
    while (current) {
      result.push(current.data);
      current = current.next;
    }
    return result;
  }

  getSize(): number {
    return this.size;
  }
}

이중 연결 리스트 노드

class DoublyListNode<T> {
  data: T;
  next: DoublyListNode<T> | null;
  prev: DoublyListNode<T> | null;

  constructor(data: T) {
    this.data = data;
    this.next = null;
    this.prev = null;
  }
}

class DoublyLinkedList<T> {
  private head: DoublyListNode<T> | null;
  private tail: DoublyListNode<T> | null;
  private size: number;

  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  // 앞에 삽입
  prepend(data: T): void {
    const newNode = new DoublyListNode(data);
    
    if (!this.head) {
      this.head = this.tail = newNode;
    } else {
      newNode.next = this.head;
      this.head.prev = newNode;
      this.head = newNode;
    }
    this.size++;
  }

  // 뒤에 삽입
  append(data: T): void {
    const newNode = new DoublyListNode(data);
    
    if (!this.tail) {
      this.head = this.tail = newNode;
    } else {
      this.tail.next = newNode;
      newNode.prev = this.tail;
      this.tail = newNode;
    }
    this.size++;
  }
}

장점

• 동적 크기: 런타임에 크기를 자유롭게 변경할 수 있다
• 효율적 삽입/삭제: 위치를 알고 있다면 O(1) 시간에 수행
• 메모리 효율성: 필요한 만큼만 메모리를 사용한다

단점

• 순차 접근: 특정 위치 접근에 O(n) 시간 필요
• 추가 메모리: 포인터 저장을 위한 추가 공간 필요
• 캐시 성능: 메모리가 연속적이지 않아 캐시 미스 발생 가능
• 포인터 관리: 포인터 조작 실수 시 메모리 누수나 오류 발생

활용 사례

일반적인 사례

• 실행 취소/다시 실행: 편집기의 히스토리 관리
• 음악/동영상 플레이리스트: 순차적 재생과 추가/제거
• 브라우저 히스토리: 뒤로/앞으로 가기 기능

다른 자료구조의 기반

• 스택 구현: 단일 연결 리스트로 구현 가능
• 큐 구현: 이중 연결 리스트로 효율적 구현
• 해시 테이블: 충돌 해결을 위한 체이닝

프론트엔드에서의 활용

React 컴포넌트 체인

// 컴포넌트 간 연결 관리
interface ComponentNode {
  id: string;
  component: React.ComponentType;
  next: ComponentNode | null;
}

class ComponentChain {
  private head: ComponentNode | null = null;

  addComponent(id: string, component: React.ComponentType): void {
    const newNode: ComponentNode = {
      id,
      component,
      next: this.head
    };
    this.head = newNode;
  }

  renderChain(): React.ReactElement[] {
    const components: React.ReactElement[] = [];
    let current = this.head;
    
    while (current) {
      const Component = current.component;
      components.push(<Component key={current.id} />);
      current = current.next;
    }
    
    return components;
  }
}

무한 스크롤 구현

interface DataNode<T> {
  data: T;
  next: DataNode<T> | null;
}

class InfiniteScrollList<T> {
  private head: DataNode<T> | null = null;
  private tail: DataNode<T> | null = null;

  append(data: T): void {
    const newNode: DataNode<T> = { data, next: null };
    
    if (!this.head) {
      this.head = this.tail = newNode;
    } else {
      this.tail!.next = newNode;
      this.tail = newNode;
    }
  }

  getPage(startIndex: number, pageSize: number): T[] {
    const result: T[] = [];
    let current = this.head;
    let index = 0;

    // startIndex까지 이동
    while (current && index < startIndex) {
      current = current.next;
      index++;
    }

    // pageSize만큼 데이터 수집
    while (current && result.length < pageSize) {
      result.push(current.data);
      current = current.next;
    }

    return result;
  }
}

배열과의 비교

특성	배열	연결 리스트
접근 시간	O(1)	O(n)
삽입/삭제	O(n)	O(1)*
메모리 사용	연속적	비연속적
캐시 성능	좋음	나쁨
구현 복잡도	낮음	높음

*위치를 알고 있을 때

최적화 팁

• 더미 헤드 노드: 삽입/삭제 로직을 단순화
• 꼬리 포인터 유지: 리스트 끝 삽입을 O(1)로 최적화
• 크기 추적: 별도 변수로 리스트 크기 관리
• 메모리 풀링: 노드 재사용으로 메모리 할당/해제 비용 절약