DFS | BFS 알고리즘

그래프 탐색에는 두가지 방법이 있다.
DFS (depth - first - search) 와 BFS (breadth - first - search)

1. DFS

정의

다음 분기로 넘어가기 전에 한 루트의 모든 노드를 방문한 후 넘어가는 방식

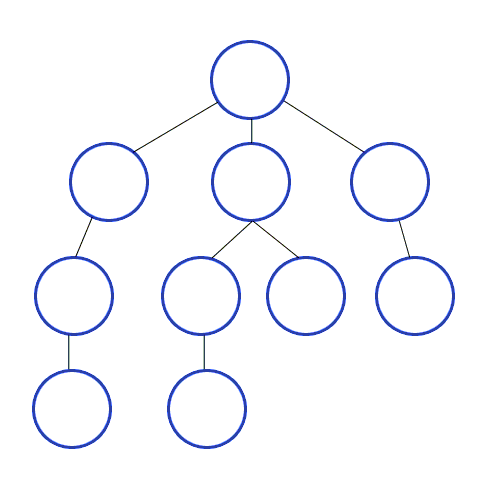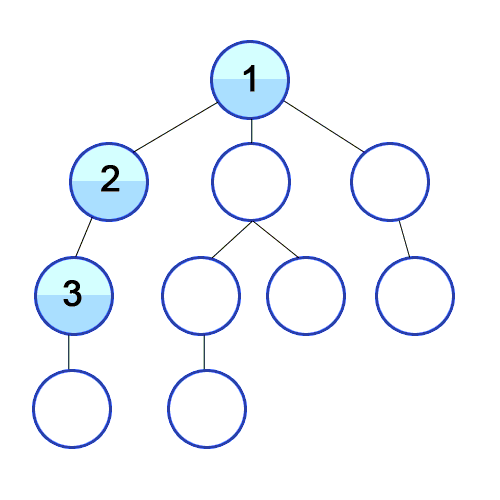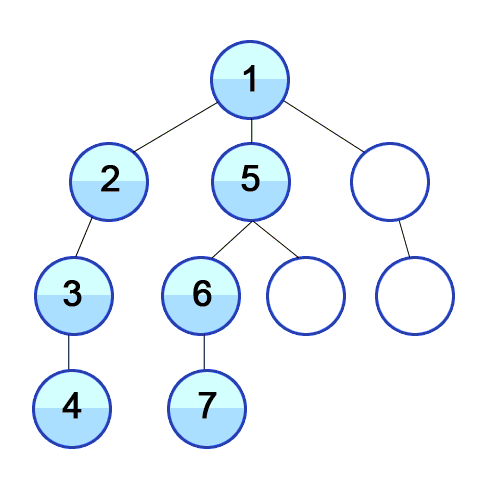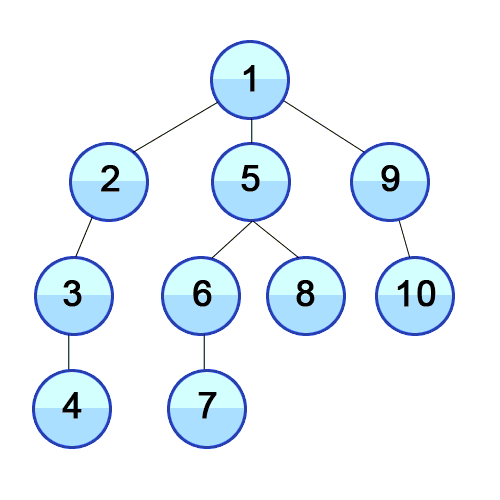
출처 https://developer-mac.tistory.com/64

특징

1) 경로의 특징을 알고자 할때
이유: 한 분기에서 루트노드는 끝까지 가보려고 하기 때문에 어떤 부분에 어떤 정점이 있는지를 알려줄 수 있음
2) 탐색하려는 그래프의 크기가 클 때
이유: 한 분기별로 간단하게 처리할 수 있음
3) 검색 속도는 느림
4) 스택 또는 재귀함수로 구현

재귀함수로 구현한 경우

class Graph {
	private int V;
    private LinkedList<Integer> adj[];

	Graph(int v) {
		V = v;
		adj = new LinkedList[v];
		for (int i = 0; i < v; ++i) {
			adj[i] = new LinkedList(); 
		}
	}
    
    void addEdge(int v, int w){
    	adj[v].add(w);
    }
    
    void DFS(int v) {
      boolean visited [] = new boolean[V];
      DFSUtil(v, visited);
	}
    
    void DFSUtil(int v, boolean visited[]){
		visitied[v] = true;
        System.out.println(v + "");
        
        Iterator<Integer> it = adj[v].listIterator();
        while (it.hasNext()) {
        	int n =it.next();
            if (!visited[n])
            	DFSUtil(n, visited);
        }
	}
}

2. BFS

정의

루트노드부터 시작하여 인접한 노드를 먼저 탐색하는 방식으로 가까운 정점부터 먼저 방문함

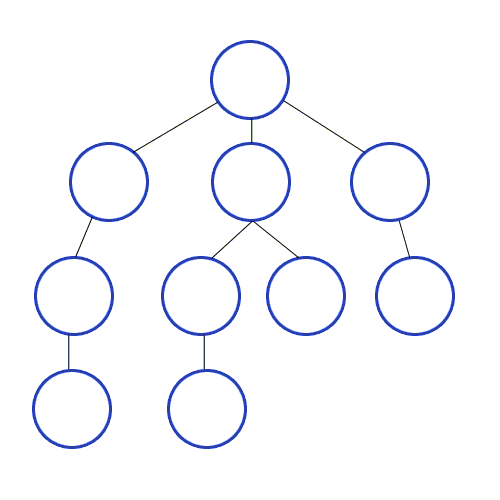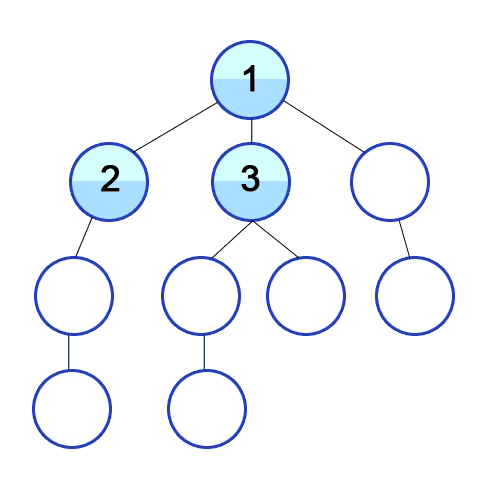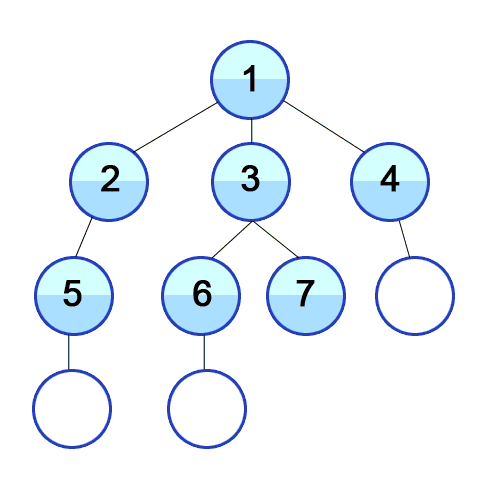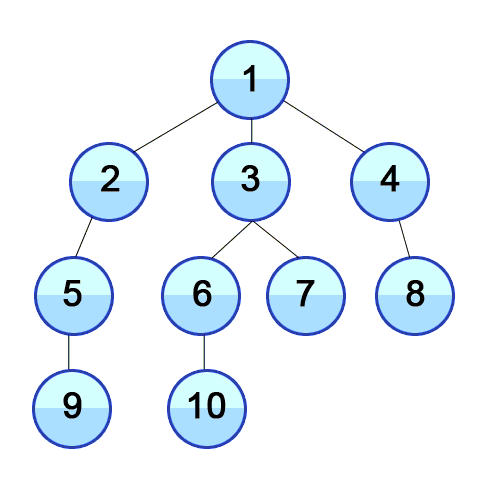
출처 https://developer-mac.tistory.com/64

특징

1) 최단 거리를 구하고자 할 때
이유: 인접한 노드부터 검색하므로 원하는 타겟까지의 바운더리를 알 수 있음
2) 탐색하려는 그래프가 별로 크지 않을때
이유: 그래프가 크지 않다는 건 그만큼 타겟이 가까운 거리에 있다는 뜻임
3) 큐로 구현

큐로 구현

class Graph {
	private int V;
    private LinkedList<Integer> adj[];
    
	Graph(int v) {
		V = v;
		adj = new LinkedList[v];
		for (int i = 0; i < v; ++i) {
			adj[i] = new LinkedList(); 
		}
	}
    
    void addEdge(int v, int w) {
    	adj[v].add(w);
    }
    
    void BFS(int s) {
    	boolean visited[] = new boolean[V];
        LinkedList<Integer> queue = new LinkedList<Integer>();
        
        visited[s] = true;
        queue.add(s);
        
        while (queue.size() != 0 ){
        	s = queue.poll();
            System.out.println(s + " ");
            
            Iterator<Integer> i = adj[s].listIterator();
            
            while (i.hasNext()) {
            	int n = i.next();
                if(!visited[n]){
                	visited[n] = true;
                    queue.add();
                }
            }
        }
    }
}