자료구조와 알고리즘 책을 읽다가 유용한 내용이 있어서 정리하려고 한다.
이 글을 읽는 사람이 있다면 기본적으로 시간복잡도에 대해 어느정도 알고 있다는 가정을 한다.
데이터를 처리하는데 있어서 연산이 얼마나 빠른가를 측정할 때는 순수하게 시간 관점에서 연산이 얼마나 빠른가가 아니라 얼마나 많은 단계가 필요한지를 논해야 한다.
누구도 어떤 연산이 정확히 5초가 걸린다고 단정할 수 없다. 같은 연산도 어떤 컴퓨터에서는 5초가 걸리고, 구형 하드웨어에서는 더 오래 걸릴 수 있으며, 미래의 컴퓨터에서는 훨씬 빠를 수 있다.
시간은 연산을 실행하는 하드웨어에 따라 항상 바뀌므로 시간을 기준으로 속도를 측정하면 신뢰 할 수 없다. 대신 연산의 속도를 측정할 때 얼마나 많은 단계(step)가 필요한가를 따져볼 수 있다.
연산 A에 5단계가 필요하고 연산 B에 500단계가 필요하면, 모든 하드웨어에서 연산 A가 연산 B보다 항상 빠를거라고 가정할 수 있다. 빅오표기법은 데이터의 크기에 따라 알고리즘의 연산이 최악의 경우 얼마만큼의 단계를 거치는지에 대한 표기이다.
Big-O
- 상수 무시
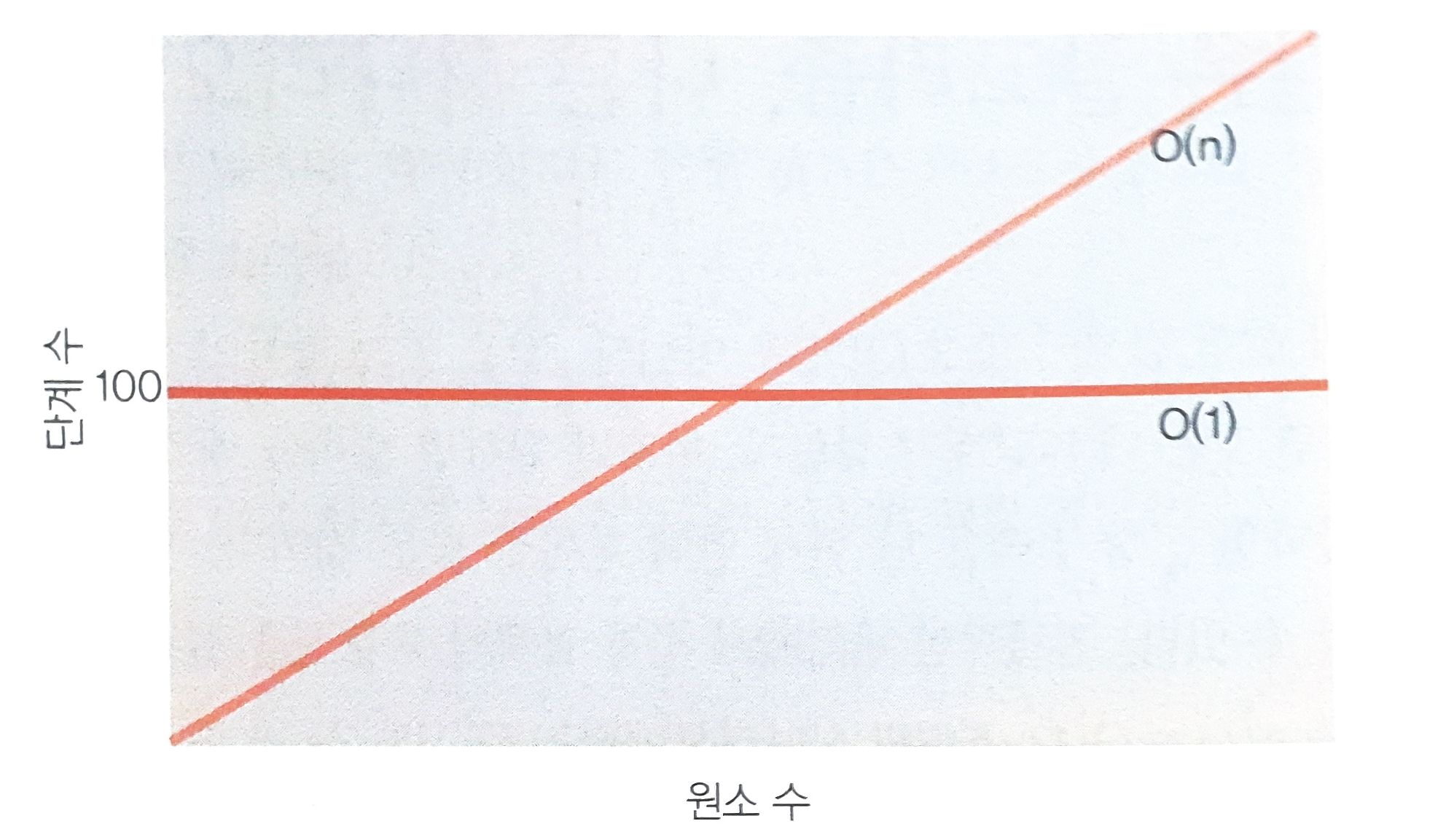
빅오표기법은 기본적으로 상수를 생략한다. 알고리즘이 데이터가 아무리 커지더라도 항상 100단계를 거친다면 O(100)이 아닌 O(1)로 표기한다. 그렇다고 O(1)이 O(N), O(N^2)보다 무조건 빠른다는 것은 아니다. O(N)과 비교했을 때 100단계까지는 O(N)이 처리가 더 빠르다. 마찬가지로 10단계까지는 O(N^2)이 처리가 더 빠르다.
하지만 핵심은 이렇다.
100보다 큰 데이터부터는 '항상 100단계가 걸리는 알고리즘' 보다 O(N) 알고리즘이 더 많은 단계가 걸린다.
변화가 생기는 일정량의 데이터가 항상 있을 것이고 O(N)은 그 순간부터 무한대까지 더많은 단계가 걸리므로 O(N)은 전반적으로 O(1)보다 덜 효율적이라고 할 수 있다.
항상 1,000,000 단계가 걸리는 O(1) 알고리즘이라도 마찬가지다. 데이터가 증가 할수록 O(N)이 O(1)보다 덜 효율적인 어떤 지점에 반드시 다다르게 되며, 이 지점부터 데이터양이 무한대로 갈 때까지 바뀌지 않는다.
그러나 시간복잡도가 같은 O(N^2)이라고 하더라도 실제 O(N^2/2)의 경우가 2배 더 빠른 처리를 한다. 아래와 같이 시간복잡도가 둘 다 O(N^2)인 버블정렬과 선택정렬을 비교해보면 이해하기 쉽다.
- 버블정렬 O(N^2)
let step = 0;
function bubbleSort(array) {
let len = array.length;
for (let i = 0; i < len; i++) {
for (let j = 0; j < len - i - 1; j++) {
// step++;
if (array[j] > array[j + 1]) {
const temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
// step++;
}
}
}
return array;
}
console.log(bubbleSort([10, 9, 8, 7, 6, 5, 4, 3, 2, 1]));
console.log(step); // 90
- 선택정렬 O(N^2)
let step = 0;
function selectionSort(array) {
for (let i = 0; i < array.length - 1; i++) {
let lowestNumberIndex = i;
for (let j = i + 1; j < array.length; j++) {
// step++;
if (array[j] < array[lowestNumberIndex]) {
lowestNumberIndex = j;
}
}
if (lowestNumberIndex !== i) {
const temp = array[i];
array[i] = array[lowestNumberIndex];
array[lowestNumberIndex] = temp;
}
// step++;
}
return array;
}
console.log(selectionSort([10, 9, 8, 7, 6, 5, 4, 3, 2, 1]));
console.log(step); // 54

빅오표기법에서는 상수를 무시하기때문에 선택정렬과 버블정렬을 정확히 같은 방식으로 설명한다. 앞선 선택정렬과 버블정렬 예제를 봤을 때 선택정렬은 엄밀히 말해 O(N^2/2) 여야하지만 단순히 O(N^2)이다. 비슷하게 O(2N)도 O(N)이고, O(N/2)도 O(N)이다. O(N)보다 100배나 느린 O(100N)이라해도 마찬가지로 O(N)이다.
빅 오로는 정확히 같은 방법으로 표현되는 두 알고리즘이 있을 때, 한쪽이 다른 한쪽보다 100배나 빠를 수 있다는 점 때문에 이 규칙은 빅 오 표기법을 완전히 쓸모없게 만들어 버리는 것처럼 보인다. 선택정렬과 버블정렬에서도 정확히 마찬가지다. 두 알고리즘 모두 빅 오로는 O(N^2)이지만 선택정렬은 사실 버블정렬보다 두배나 빠르다. 정말로 두 알고리즘 중 하나를 골라야 한다면 선택정렬이 더 나은 선택이다.
빅오의 역할
빅 오는 버블정렬과 선택 정렬간에 차이를 두지 않지만, 알고리즘의 장기적인 증가율을 분류하는 훌륭한 방법이기에 여전히 매우 중요하다. 다시말해, 어느 정도 크기의 데이터에 대해서는 O(N)이 항상 O(N^2)보다 빠르다. O(N)이 실제로 O(2N)이든 심지어 O(100N)이든 결과적으로 항상 그렇다.
O(100N)이 O(N^2)보다 빨라지는 어느 정도 크기의 데이터가 꼭 있기 마련이다. 이게 바로 빅 오가 상수를 무시하는 이유다. 빅 오는 특정시점부터 어떤 유형이 다른유형보다 속도가 빨라지고 이후로도 계속해서 더 빠른 경우 두 유형을 다르게 분류하고자 한다. 하지만 정확한 시점은 빅 오에서 중요하지 않다.
따라서 O(100N) 같은 유형은 사실 없다. O(N)이라고 쓸 뿐이다.
마찬가지로 데이터가 크다면 주어진 O(log N) 알고리즘이 원래는 O(2log N)일지라도 O(log N)이 O(N)보다 항상 빠르다.
빅 오는 데이터가 많을 때 한 알고리즘이 어떤 시점부터 다른 알고리즘보다 더 빠름을 보장하므로 빅 오에서 서로 다른 분류에 속하는 두 알고리즘이라면 어떤 알고리즘을 써야 할지 대체로 알 수 있으며, 따라서 빅 오는 매우 유용한 도구다.
하지만 중점적으로 이해해야 할 내용은 두 알고리즘이 같은 분류에 속하더라도 반드시 두 알고리즘의 처리 속도가 같지 않다는 점이다. 버블정렬과 선택정렬은 둘다 O(N^2)이지만 어쨌든 버블 정렬은 선택 정렬보다 두배 느리다. 따라서 빅 오에서 다른 분류에 속하는 알고리즘을 대조할 때는 빅 오가 완벽한 도구지만, 같은 분류에 속하는 두 알고리즘이라면 어떤 알고리즘이 더 빠를지 알기 위해 더 분석해야 한다.
평균적인 시나리오의 경우엔?
삽입정렬의 경우 시간복잡도는 O(N^2)이다. 엄밀히 따지면 O(N^2+N-2)이다. 그렇기 때문에 항상 O(N^2/2)의 효율을 가지는 선택정렬보다 느리다. 단 이것은 최악의 시나리오의 경우에서다. 실제로 최악의 시나리오와 최선의 시나리오는 드물게 일어난다.
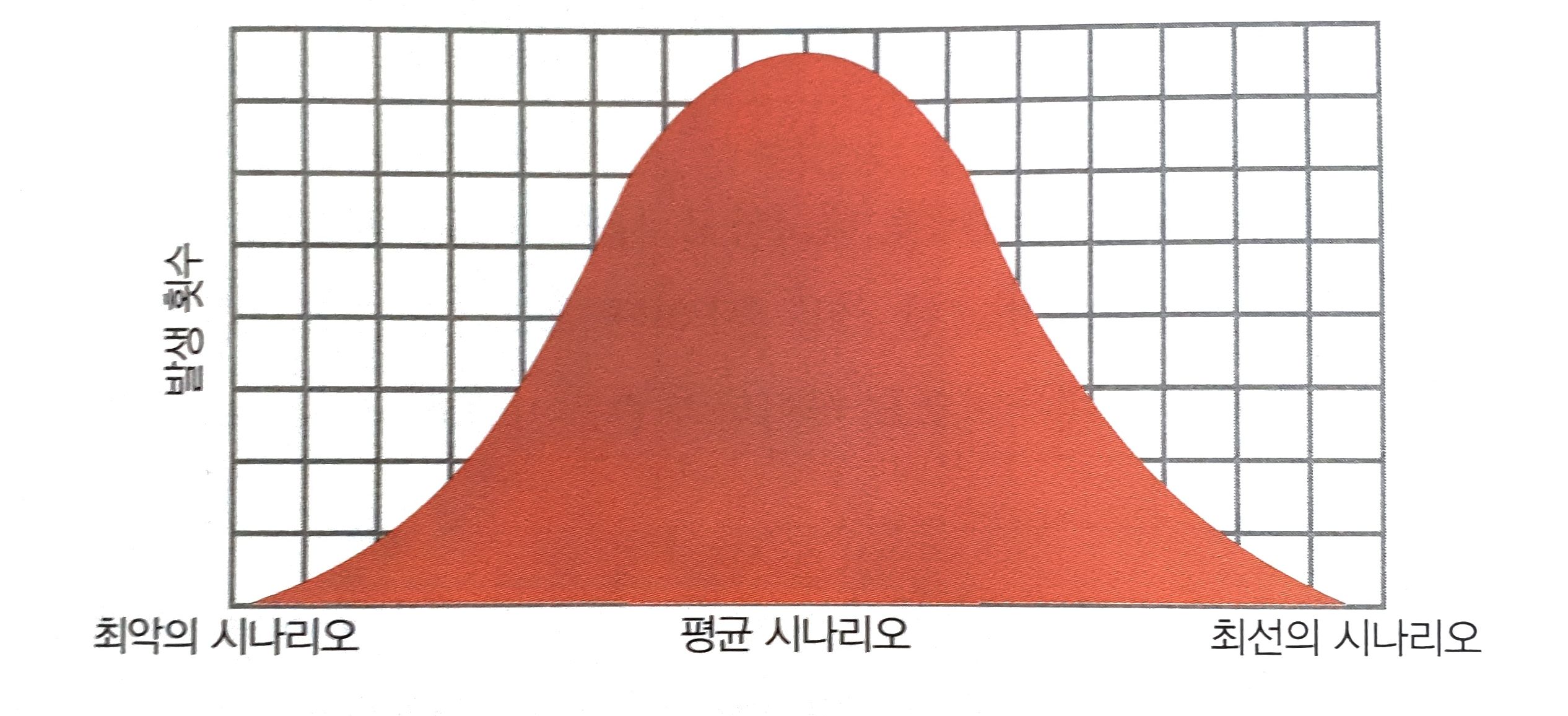
모든 시나리오 관점에서 삽입정렬을 검토해보면 최악은O(N^2), 평균은 O(N^2/2), 최선은 O(N)이다. 이렇게 서로 다른 까닭은 삽입정렬에서는 데이터를 비교하는 어떤 패스스루에서는 이미 정렬 된 상태라면 패스스루가 일찍 종료되기 때문이다.
선택정렬은 모든 시나리오에서 O(N^2/2)이다. 선택정렬에서는 어떤 시점에서 미리 패스스루를 끝낼 메커니즘이 전혀 없기 때문이다.
그렇다면 선택정렬과 삽입정렬 중 어떤게 더 나을까? 정답은 음.. 경우에 따라 다르다.
임의로 정렬된 배열 같은 평균적인 경우라면 두 정렬은 유사하게 수행된다. 거의 정렬된 데이터를 다룰 거라고 가정할 수 있는 이유가 있다면 삽입 정렬이 더 낫다. 대부분 역순으로 정렬된 데이터를 다룰 거라고 가정할 수 있는 이유가 있다면 선택정렬이 더 빠르다. 데이터가 어떨지 전혀 알 수 없다면 기본적으로 평균적인 경우이며 둘 다 같다.
이처럼 최악의 시나리오에서 효율이 좋지않은 알고리즘이더라도 모든 시나리오를 검토했을때, 데이터에 따라 더 좋은 성능을 기대 할 수 있는 근거가 있다면 삽입정렬을 선택 할 수도 있다.
이 내용들은 정렬에 대해 알아보고자 하는 내용이 아니다. Big-O 표기법에 따라 같은 유형의 알고리즘이더라도 더 효율이 좋은 알고리즘이 있고, for문에서 break를 이용한다던지 원하는 결과를 얻었을 때 불필요한 검색을 없애 평균적인 시나리오에서의 성능을 높일 수 있음을 인지하는 것이 중요하다. 내가 선택한 알고리즘보다 더 효율이 좋은 알고리즘이 있는지, 혹은 최적화 할 수 있는 방법이 있는지 항상 고민 해 볼 부분이라고 생각한다.
마무리
지금까지 시간복잡도에 대해 '이거는 O(N^2)이고 저거도 O(N^2)이니까 걸리는 시간은 똑같아'라고 생각하고있었다. 같은 연산을 하는데 극단적으로 1000000N^2 과 N^2을 놓고 본다면 N^2이 백만배는 더 빠른 처리를 할 수 있는데 말이다. 데이터에 따라서는 O(N)보다 O(N^2)이 더 효율이 좋을수도, 같은 시간복잡도라도 무조건 같은 효율성을 갖지 않는다는것을 알고 있어야 한다고 생각이 들었다.

감사합니다. 매우 좋은 글입니다!