탐색
- 주어진 자료들 중에 원하는 조건에 해당하는 자료를 찾는 과정
- 주어진 자료들을 모아둔 공간(탐색 공간)에서 목표 값을 찾는 과정
모든 알고리즘의 3가지 공통 구성요소
-
탐색 목표
: 타겟 데이터(값)
-> 탐색 성공 여부 판단의 기준 -
탐색 공간
: 탐색 목표일 가능성이 있는 것을 모아 놓은 집합
- 탐색(검색) 알고리즘
: 탐색을 진행하며 따라야하는 특정 절차 및 지침을 모아둔 집합
탐색 문제 해결방법
1. 선형 탐색 알고리즘 = 순차 탐색 알고리즘

- 순서대로 하나씩 탐색하며 탐색 타겟 찾기
->원하는 값 발견시, 나머지는 안봄 - 완전 탐색법 중 하나
(완전탐색? <- 선형 검색 외에 완전탐색하는 방법들은 위 링크에서 다룸) - 시간 복잡도
최선 = O(1) -> 한번에 찾음
최악 = O(n) -> 타겟 못 찾음
2. 이진(이분) 탐색 알고리즘
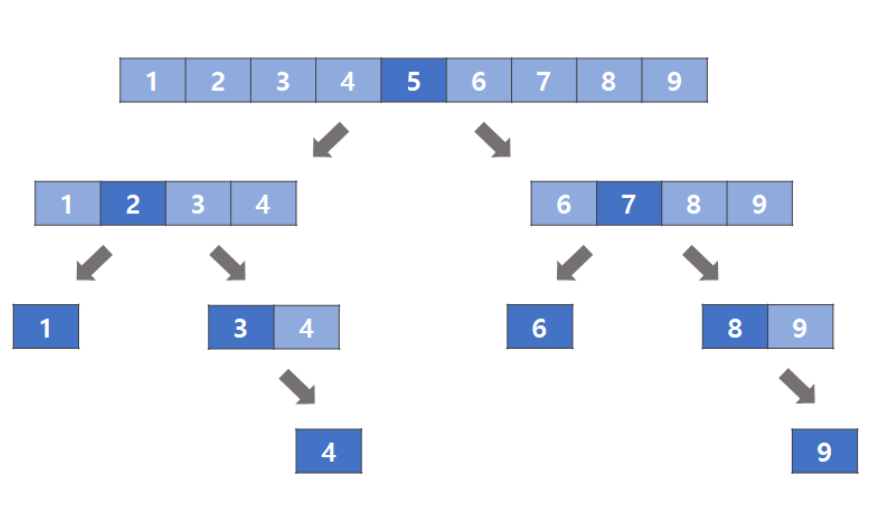
- 중간값 찾아서 -> 왼쪽 오른쪽 구분
계속 중간값을 찾아 반씩 나눠서 탐색 - 정렬된 리스트에서 특정 값 위치를 탐색하는 알고리즘
- 시간 복잡도
최선 : O(1) -> 한번에 찾음
최악 : O(log2n) -> 타겟 못찾음
-> 보통 정렬된 리스트에는 이진탐색
-> 정렬되지 않은 리스트에는 선형 탐색 사용
3. 해시 탐색
- 해시 : 잘게 썬다, 자른다
- 선형/이진 탐색은 어떤 값이 어떤 인덱스에
들어있는지 정보가 없을 때 사용
-> 데이터랑 데이터와 같는 첨자의 요소에 넣어두면 한번에 찾는게 가능하지 않을까? 란 아이디어가 떠오름
-> 해시 탐색은 값-인덱스 미리 연결해두어 더 짧은 시간에 탐색 가능
- 해시 탐색은 해시 함수를 사용하여
1) 입력들을 분류 및 저장
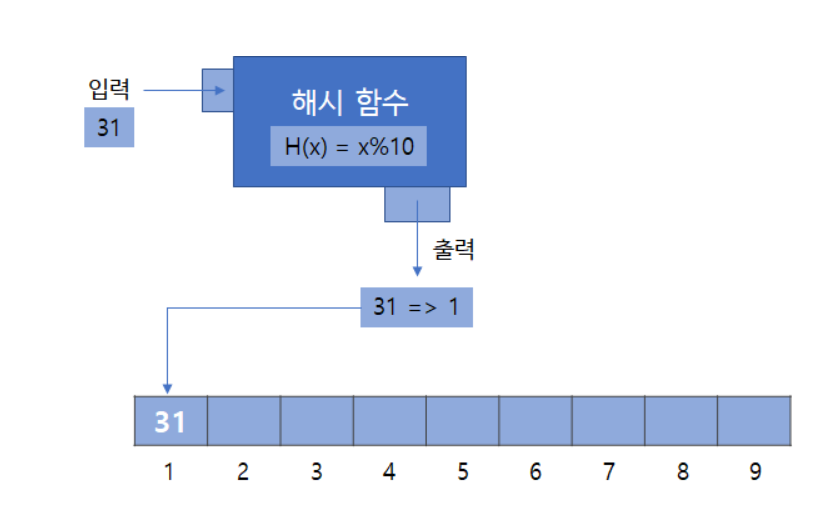
-> 입력.분류하는 과정
= 해시테이블(미리 준비해둔 상자)에 입력/분류하여 담아두는 과정
2) 요소를 탐색(검색)
하는 두개의 알고리즘이 필요
- 해시 값 충돌 (해시 값이 겹치는 경우)
-> 해결방법으로 같은 해시 값을 가지면 해당 요소들을 연결 리스트로 만듦
-> 해시 충돌시에 조사하게 되는 대체칸 = 번지 계열
-> 번지 계열이 겹쳐 충돌일어날 경우 = 클러스터 발생 - 시간복잠도
최선 : O(1)
최악 : O(n)
검색 알고리즘 중에서 매우 속도가 빠른 알고리즘
해시함수의 질이 좋을 때 사용이 권장됨
4. 이진 탐색 트리 = BST
-
정의
왼쪽 서브트리의 키값들은 root의 키값보다 작다
오른쪽 서브트리의 키값들은 root의 키값보다 크다
왼쪽, 오른쪽 서브트리들은 각각 모두 BST정의를 만족한다
BST의 모든 node들의 키값은 unique하다.
위의 4가지를 모두 만족해야 한다. -
탐색 알고리즘
어떠한 BST에서 원하는 값을 찾고자할 때,root값을 기준으로
원하는 값 > root 키 값 : 오른쪽 서브트리로 이동
원하는 값 < root 키 값 : 왼쪽 서브트리로 이동
원하는 값 = root 키 값 : 탐색 종료
이 것을 계속 반복해나가면 된다.
-> 이진 탐색 트리는 트리 구조와 함께
추후 게시물에서 추가적으로 다뤄
관련 링크 첨부 예정 + 관련 내용 수정 예정
참고
탐색 알고리즘 - 선형탐색/이진탐색
[탐색&자료구조] 👀완전탐색(exhaustive search) 알고리즘 + 📂배열(array)
[알고리즘] 탐색 알고리즘 (선형, 이분, 해시, BST)
[c++] 알고리즘 개념공부 :: 탐색 (선형 탐색, 이진 탐색, 해시 탐색)
탐색 알고리즘을 알아봅시다!!:)
