자료구조_그래프

그래프란?

• 데이터 간 관계를 표현하기 위한 자료구조 중 하나
• 비선형 구조 + 트리의 일반적 개념
  (트리도 일종의 그래프)
  
  
• 그래프(G) = (V,E)의 쌍
  V = 정점(vertex)의 집합
  E = 간선(edge)의 집합
  
  
• 정점 =노드(N)와 노드를 연결하는 간선(E)을 하나로 모아 놓은 자료구조
  

---

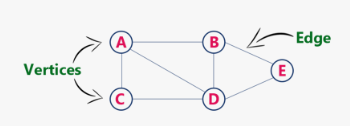
그래프 구성요소

1) 정점 = 노드

• 독립된 개체로 동그라미로 표현
• 일반적으로 숫자나 이름으로 구분
• 데이터가 저장되어있음

2) 간선 = link = branch

• 노드를 연결하는 선
• 위치 간의 관계

3) 인접 정점(adjacent vertex)

• 간선에 의 해 직접 연결된 정점

4) 정점의 차수(degree)

• 무방향 그래프에서 하나의 정점에 인접한 정점의 수
• 무방향 그래프에 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배

5) 진입 차수(in-degree) = 내차수

• 방향 그래프에서 외부에서 오는 간선의 수

6) 진출 차수(out-degree) = 외차수

• 방향 그래픙에서 외부로 향하는 간선의 수
• 방향 그래프에 있는 정점의 진입 차수 또는 진출 차수의 합
  = 방향 그래프의 간선의 수(내차수 + 외차수)

7) 경로 길이(path length)

• 경로를 구성하는 데 사용된 간선의 수

8) 단순 경로(simple path)

• 경로 중에서 반복되는 정점이 없는 경우

9) 사이클(cycle)

• 단순 경로의 시작 정점과 종료 정점이 동일한 경우

---

그래프 특징

---

그래프 종류

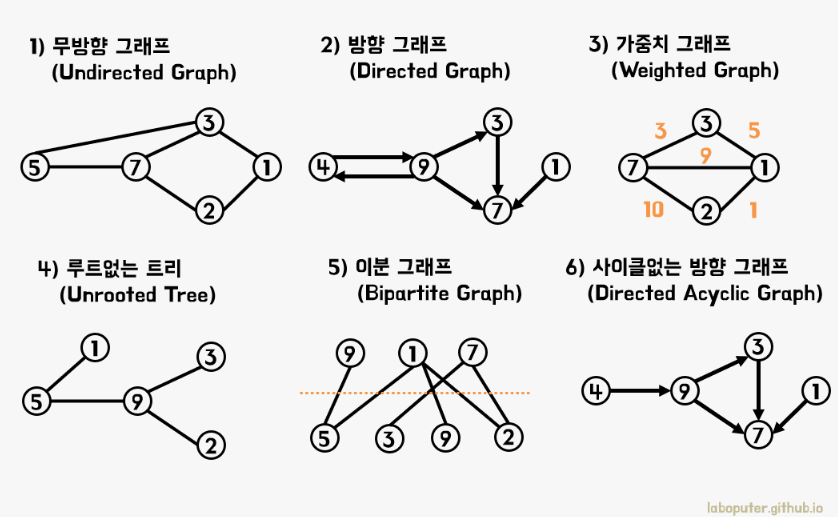
1) 무방향 그래프

• 간선의 방향이 없음
  = 간선을 통해 양방향으로 갈 수 있음
• A와 B를 연결하는 간선 = (A,B) = (B,A)

2) 방향 그래프

• 간선에 방향이 있음
• A>B로 가는 간선 = <A,B> != <B,A>

3) 가중치 그래프

• 간선에 비용 또는 가중치가 할당된 그래프
• 네트워크라고 함

4) 루트없는 트리

• 간선을 통해 정점 간 잇는 방법이 한가지인 그래프
  -> 트리의 정의

5) 이분 그래프

• 그래프의 정점을 겹치지 않게 두 그룹으로 나눈 후 다른 그룹끼리만 간선이 존재하게 분할할 수 있는 그래프

6) 사이클이 없는 방향 그래프

• 정점에서 출발해 자기 자신으로 돌아오는 경로(사이클)가 없는 그래프

7) 연결 그래프(Connected Graph)

• 무방향 그래프에 있는 모든 정점쌍에 대해서 항상 경로가 존재하는 경우
  (트리(Tree): 사이클을 가지지 않는 연결 그래프)

8) 비연결 그래프(Disconnected Graph)

• 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우

9) 사이클(Cycle)

• 단순 경로의 시작 정점과 종료 정점이 동일한 경우
• 단순 경로(Simple Path): 경로 중에서 반복되는 정점이 없는 경우

10) 완전 그래프(Complete Graph)

• 그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
• 무방향 완전 그래프
  정점 수 = n이면 간선의 수: n * (n-1) / 2

---

그래프의 표현

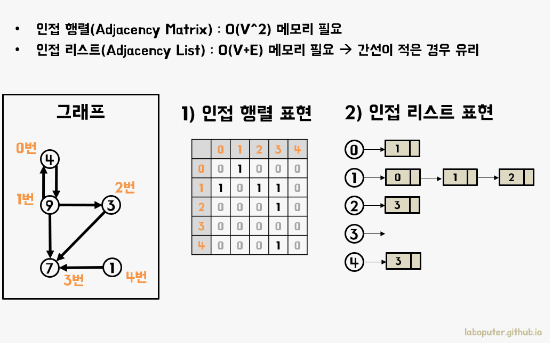
1) 인접 행렬

• 가장 일반적 표현 방법
• 2차원 배열로 정점 간의 간선의 존재 여부를 1 또는 0으로 표현
• 정점의 번호만 알면, 배열의 이넥스로 각 정점의 연결리스트에 쉽게 접근 가능
• 무방향 그래프에 간선은 두 번 저장됨

2) 인접 리스트

• 정점 개수만큼 리스트를 만들어 각각의 정점 리스트에 간선 추가
• NxN 불린 행렬(Boolean Matrix)로써 matrix[i][j]가 true라면 i -> j로의 간선이 있다는 뜻
• 무방향 그래프를 인접 행렬로 표현한다면 이 행렬은 대칭 행렬

---

그래프의 선택

1) 인접 리스트

• 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 사용
• 장점
  어떤 노드에 인접한 노드들 을 쉽게 찾을 수 있음
  그래프에 존재하는 모든 간선의 수 는 O(N+E) 안에 알 수 있다.
  : 인접 리스트 전체를 조사함
• 단점
  간선의 존재 여부와 정점의 차수: 정점 i의 리스트에 있는 노드의 수 즉, 정점 차수만큼의 시간이 필요

2) 인접 행렬

• 그래프에 간선이 많이 존재하는 밀집 그래프(Dense Graph) 의 경우
• 장점
  두 정점을 연결하는 간선의 존재 여부 (M[i][j])를 O(1) 안에 즉시 알 수 있음
  정점의 차수 는 O(N) 안에 알 수 있다. : 인접 배열의 i번 째 행 또는 열을 모두 더함
• 단점
  어떤 노드에 인접한 노드들을 찾기 위해서는 모든 노드를 전부 순회해야함
  그래프에 존재하는 모든 간선의 수는 O(N^2) 안에 알 수 있음
  : 인접 행렬 전체를 조사함