[C++] 백준 1697번 숨바꼭질

문제

문제 유형: 그래프 이론 그래프 탐색 너비 우선 탐색
난이도: 실버1

수빈이가 N의 위치에서 동생을 찾기 위해서 K의 위치까지 가야한다.
수빈이가 갈 수 있는 방법은 총 세 가지가 있고, 한 방법을 쓸 때마다 1초가 소요된다.

1. 수빈이가 지금 위치에서 +1 이동한다.
2. 수빈이가 지금 위치에서 -1 이동한다.
3. 수빈이가 지금 위치에서 *2 이동한다.

가장 빠르게 K까지 갈 수 있는 시간은 몇 초 후일까?

풀이

우선, '최단 시간'을 구한다는 것에서 BFS, DFS를 떠올릴 수 있다.
해당 문제에서는 동일 시간(동일 그래프 깊이) 내에서 가장 빨리 도착하는 경우가 최단 시간(최단 깊이)이므로 BFS를 사용하는 것이 적합하다.

수빈이가 기존 위치에서 이동하는 경우는 총 3가지이다.
즉, 노드 3개로 펼쳐나갈 수 있다.

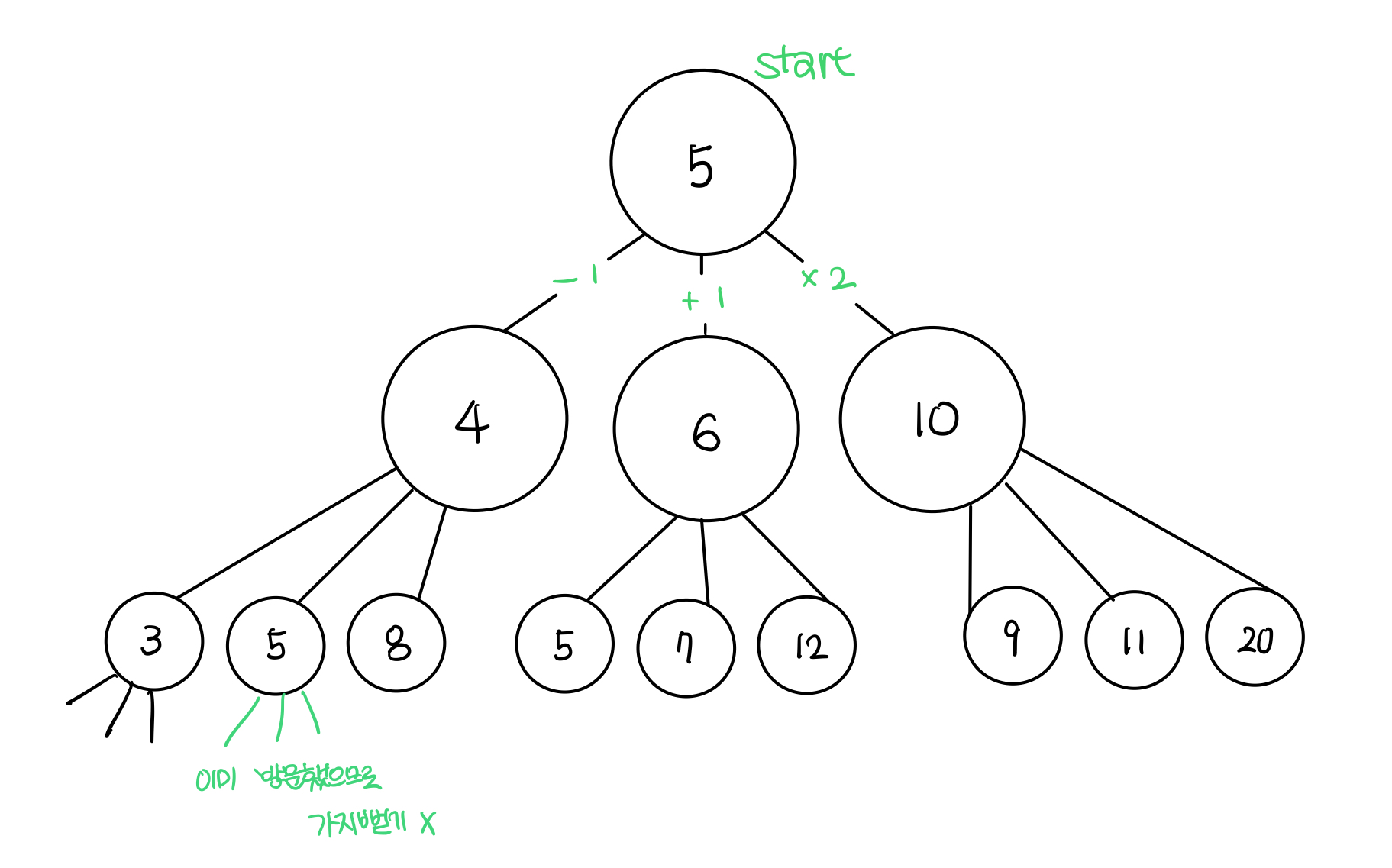
위의 방식대로 작동한다고 이해하면 쉽다.

✨ 주의할 점
1. 큐에 들어갈 정보는 방문 위치, 소요 시간이다.
따라서 pair<int, int> 을 사용한다.
2. 이미 방문한 곳을 판별하기 위해 bool visit[]을 선언한다.
3. 방문한 곳이 동생의 위치와 같으면 탐색을 종료한다.

코드

#include <iostream>
#include <queue>
using namespace std;

int n, k;
bool visit[100001]; // 방문 체크

void bfs(int start){
    queue<pair<int, int>> q; // <수빈이의 위치, 소요 시간>
    q.push(make_pair(start, 0)); // start 지점에서 0의 시간에 시작

    while(!q.empty()){
        int x = q.front().first; // x : 위치
        int cnt = q.front().second; // cnt : 시간
        q.pop();

        if(x == k){
            cout << cnt;
            break;
        }
        if(x + 1 >= 0 && x+1 < 100001){
            if(!visit[x+1]){
                visit[x + 1] = true;
                q.push(make_pair(x + 1, cnt + 1));
            }
        }
        if( x-1 >= 0 && x-1 < 100001){
            if(!visit[x-1]){
                visit[x - 1] = true;
                q.push(make_pair(x - 1, cnt + 1));
            }
        }
        if( 2*x >=0 && 2*x < 100001){
            if(!visit[2*x]){
                visit[2*x] = true;
                q.push(make_pair(2 * x, cnt + 1));
            }
        } // 모두 탐색
    }
}
int main(){
    cin >> n >> k;
    bfs(n);
    return 0;
}