https://www.youtube.com/watch?v=CS4cs9xVecg&list=PLkDaE6sCZn6Ec-XTbcX1uRg2_u4xOEky0
Andrew Ng 의 Machine Learning Course 01의 Week 1 ~ Week 2 를 수강하고 정리하였습니다.
Introduction
What is a Neural Network?
Housing Price Prediction example
Tiny neural network:
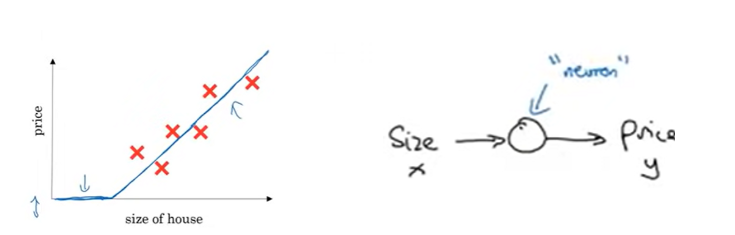
By stacking many neurons, you can get a bigger neural network:

X는 input layer, y는 output layer, X, y 사이의 neurons는 hidden layer이다.
Supervised Learning with a Neural Network
supervised learning needs input X and output y:
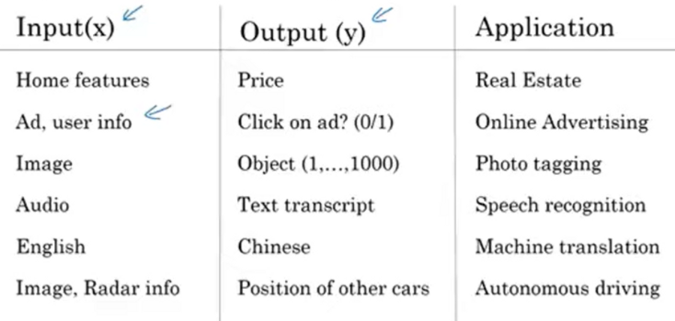
→ selecting X and y is important
- Real Estate and Online Advertising uses standard neural network
- Photo taggin uses CNN
- Speech Recognition and Machine translation uses RNN (1-d sequence data에 RNN 잘 사용)
- Autonomous driving uses Custom/Hybrid architecture (input으로 Image, Radar 등 다양한 정보가 들어가므로)
Neural Network examples

Structured data and unstructured data

rise of neural network → computers can understand unstructured data much better!
Why is deep learning taking off?
Scale drives deep learning progress
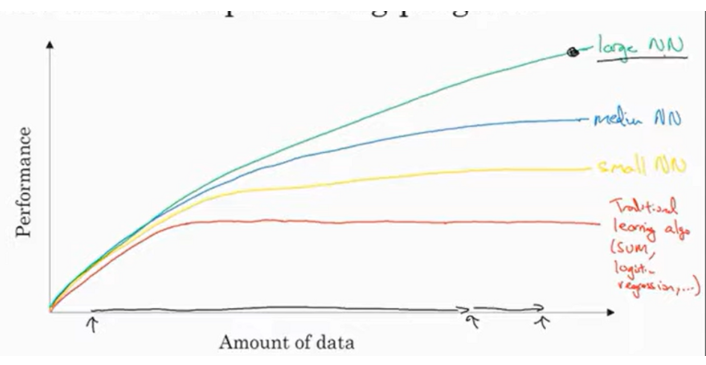
- Traditional learning algorithms as SVM, performance improves when amount of data increases but at some point it flattens.
- last 20 years, amount of data has rapidly increased!
- As for Neural Network, the larger the neural network, the performance increases more as amount of data gets larger.
m: number of training examples (size of training data)
⇒ Scale of data (m) drives deep learning progress!
- data (m)
- computation
- algorithms

using sigmoid function → 그래프 양 끝의 gradient가 0에 가까워 learning 속도가 매우 느려진다. (parameter가 천천히 바뀌기 때문)

ReLU 사용 → sigmoid를 사용했을 때보다gradient descent가 훨씬 빨라졌다
Basics of Neural Network programming
forward propagation and backward propagation
Binary Classification
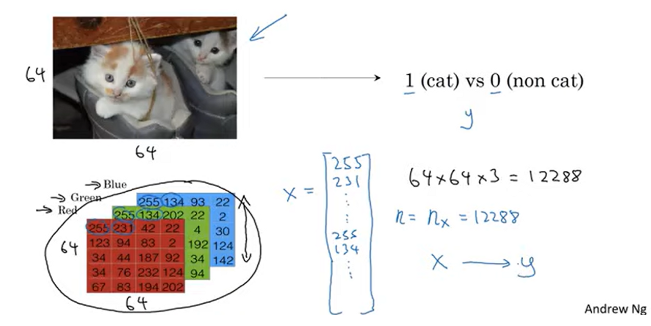
pixel intensity values → input feature vector x 로 바꾸려면 먼저 featue vector x 를 define 해야 한다.
Notation

- x is n_x dimensional feature vector
- y is 0 or 1
- m training examples
define a matrix X and stack m training examples as columns
- n_x rows
- m columns
- X.shape = (n_x, m)
define Y matrix
- Y.shape = (1, m)
Logistic Regression

Given input feature vector x, want y^ to be P(y=1|x), which means the chance of the given x to be a cat picture.
with given x and parameters are w and b, how do we generage output y^?
- y^ = 와 같은 식을 사용해 구할 수 있지만, y^이 0~1 의 값을 가지게 하고 싶다면
- y^ = 처럼 sigmoid 를 사용해야 한다.
Logistic Regression cost function
model output인 y^ 와 ground truth인 y 를 비교해 loss 계산

terminoloogy:
- Loss function is applied to just single training example
- cost function is the cost of your parameters (w, b)
Gradient Descent

parameter w, b에 따른 cost function J(w, b)
⇒ J(w, b) 가 minimum인 w, b를 찾는 것이 목적이다.
one local minima → convex function
many local minima → nonconvex function
gradient descent : from initialized value, step downhill and find minima!

: actual update of w and b
derivative를 뜻하는 d는 partial derivative를 뜻하는 다른 기호로 나타내지기도 한다.
Derivatives

derivative = slope = height/width
at a = 2, slope is 3
at a = 5, slope is also 3
More Derivatives Examples
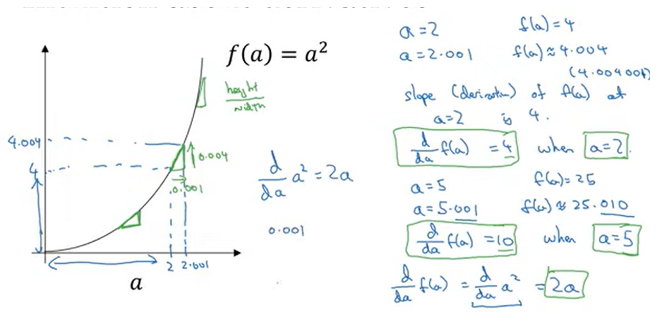
at a = 2, slope is 4
at a = 5, slope is 10
derivative of a^2 is 2a (Calculus)

Computation Graph
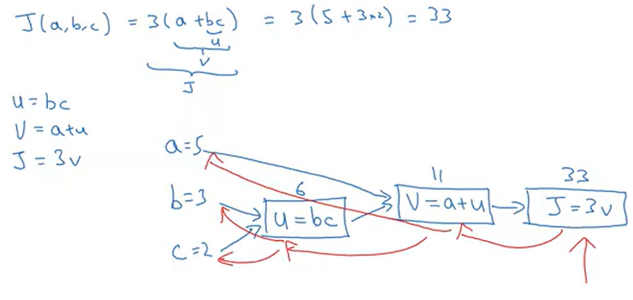
- computing J(a, b, c) needs three steps: u, v, J
- blue arrow : forward pass
- red arrow : backward pass
Computing derivatives

if you change a, value of v changes and therefore changes J.
dJ/da 를 구하기 위해서는 dJ/dv 와 dv/da 를 먼저 구해야 한다 ⇒ backward propagation
- final output variable is J in this graph.
- you want to calculate dJ/dvar
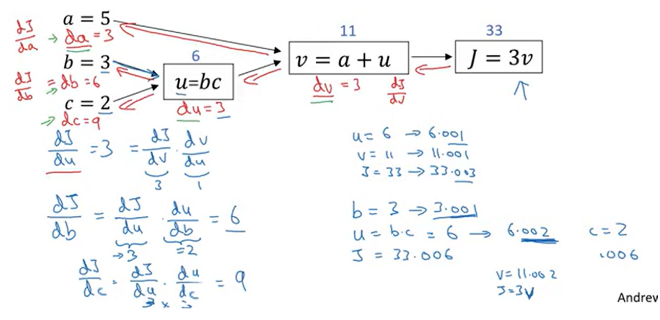
dJ/du is dJ/dv * dv/du
using chain rule, dJ/db = dJ/du * du/db
dJ/dc = dJ/du * du/dc
⇒ to compue all the derivatives, most effecient way is to compute from right to left. (backward propagation)
Logistic Regression Gradient Descent

→ draw computational graph

→ modify w and b to reduce L(a, y) by going backward to compute derivatives
- compute derivative da = dL/da = -y/a + (1-y)/(1-a)
- compute derivative dz = dL/dz = dL/da * da/dz = a - y
- dL/dw1 = x1 * dz
- dL/dw2 = x2 * dz
- db = dz
Gradient Descent on m Examples
Logistic regression on m examples

cost function J(w, b) is average of individual losses.
derivative of cost function J(w, b) is also average of derivatives of individual losses.

we are using dw_1, dw_2, db as accumulators.
after the algorithm, we can update parameters w_1, w_2, b.
for loops
- for i=1 to m
- for each features (dz, dw_1, dw_2, db, …)
Vectorization can get rid of for loops → efficient!
Vectorization
What is vectorization?

Non-vectorized implementations → for loops → very slow
vectorized → faster
demo
More Vectorization Examples
Neural network programming guideline
Whenever possible, avoid explicit for-loops:

Vectors and matrix valued functions

Logistic regression derivatives

Vectorizing Logistic Regression

define X
and define Z
and define A
Vectorizing Logistic Regression’s Gradient Computation
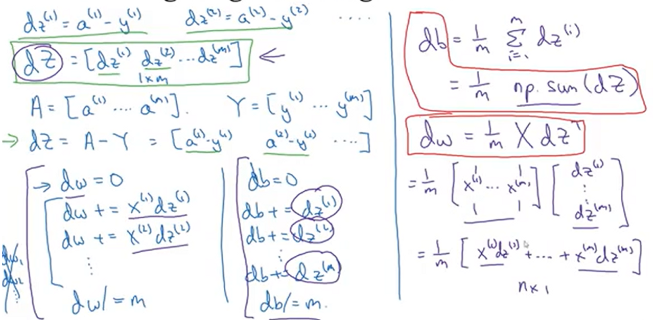
based on the definitions of dZ, we can compute this by one line of code!

→ implementing logistic regression
Broadcasting in Python
Broadcasting example

- calculate percentage of callories from carb, protein, fat for each food.
- carb in apples = 16/59 → 90%
- do this without for-loop! Google Colaboratory
cal = A.sum(axis = 0) percentage = 100*A/(cal.reshape(1,4)) # you don't have to call reshape command. # why? broadcasting

- (4, 1) + (1, ) ⇒ (4, 1) + (4, 1)
- (2, 3) + (1, 3) ⇒ (2, 3) + (2, 3)
- (m, n) + (m, 1) ⇒ (m, n) + (m, n)
General Principle

A Note on Python/Numpy Vectors

illimate rank 1 array!!
Explanation of Logistic Regression’s Cost Function (Optional)
Logistic regression cost function


Cost on m examples
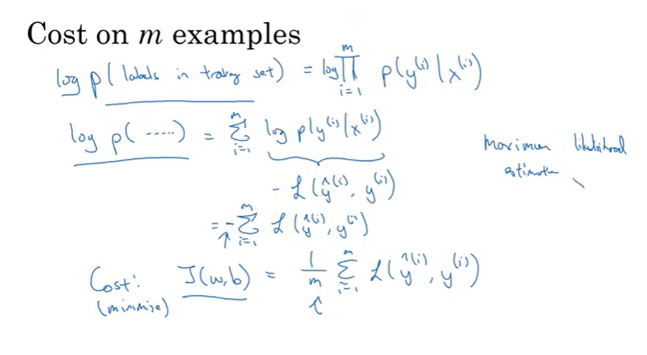

많은 것을 배웠습니다, 감사합니다.