[알고리즘] DFS(깊이 우선 탐색) & BFS(너비 우선 탐색)

Gaanii·2024년 10월 22일

BFS DFS TIL python 알고리즘

Algorithm

목록 보기

13/17

그래프란 ?

단순히 노드(N, node)와 그 노드를 연결하는 간선(E, edge)을 하나로 모아 놓은 자료 구조

그래프 관련 용어

정점(vertex): 위치라는 개념. (node 라고도 부름)
간선(edge): 위치 간의 관계. 즉, 노드를 연결하는 선 (link, branch 라고도 부름)
정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
무방향 그래프에 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배
경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우

그래프의 탐색

그래프를 탐색한다는 말은 하나의 정점으로부터 시작해서 차례대로 모든 정점들을 한 번씩 방문하는 것을 의미한다.

1-1. DFS(Depth First Search, 깊이 우선 탐색)

Root Node 혹은 다른 임의의 Node에서 다음 분기(Branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다.

모든 노드를 방문하고자 하는 경우에 DFS를 사용하고, BFS보다 좀 더 간단하지만 검색 속도 자체는 BFS에 비해 느리다 ..

DFS
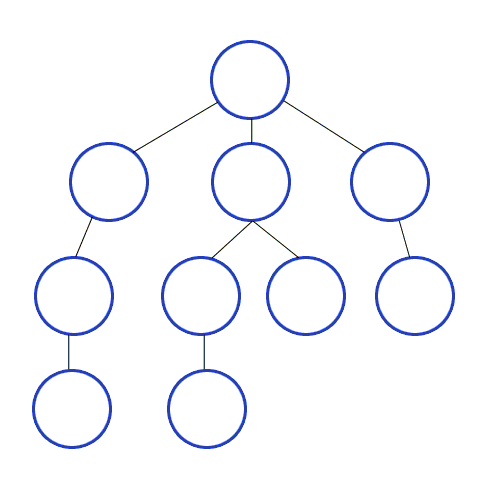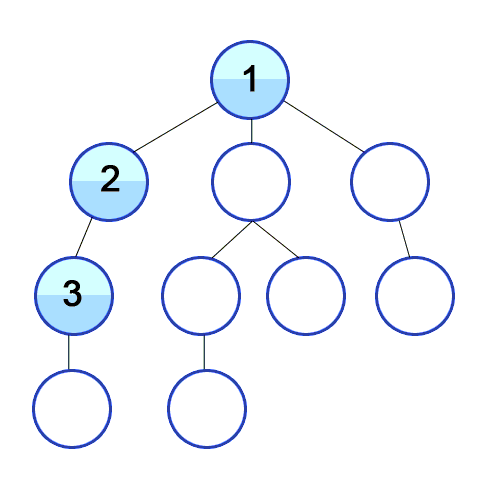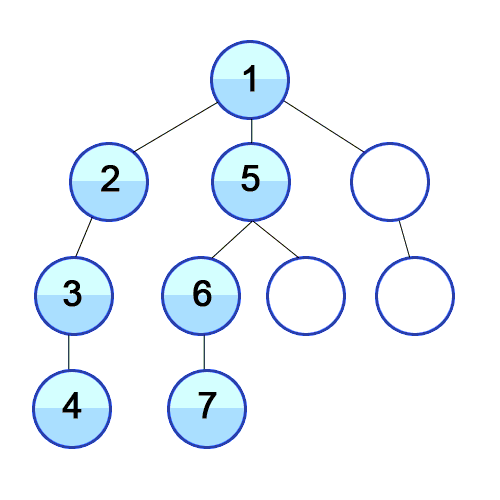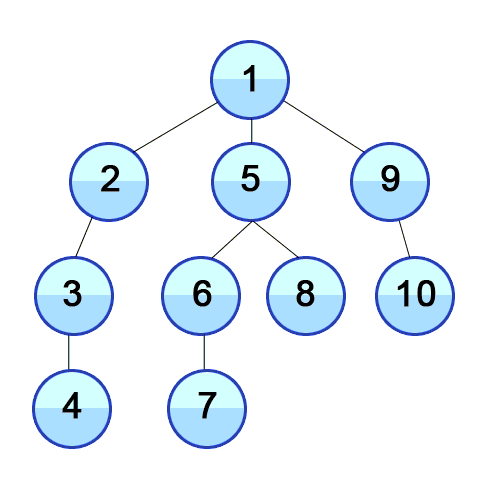
출처 : https://developer-mac.tistory.com/64

1-2. DFS Python 구현

def dfs(v):
    # 현재 노드 방문 처리
    visited[v] = True
    print(v, end=' ')
    
    # 그래프를 순환하면서 인접 노드들을 방문
    for i in graph[v]:
        # 만약 방문하지 않은 노드가 있다면
        if not visited[i]:
            # 탐색 시작
            dfs(i)

2-1. BFS(Breadth-First Search)

Root Node(혹은 다른 임의의 노드)에서 시작해서 인접한 Node를 먼저 탐색하는 방법으로, 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 방법이다.

주로 두 노드 사이의 최단 경로를 찾고싶을 대 BFS를 사용한다.

BFS
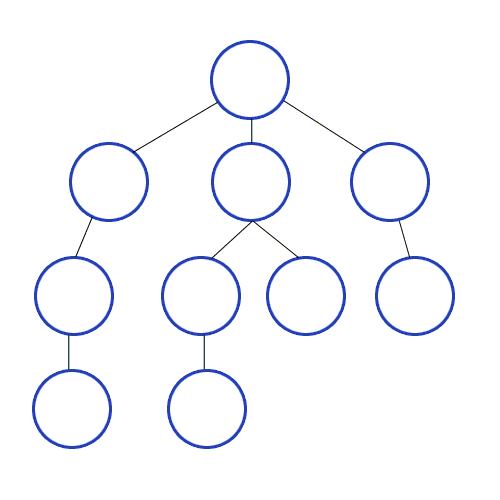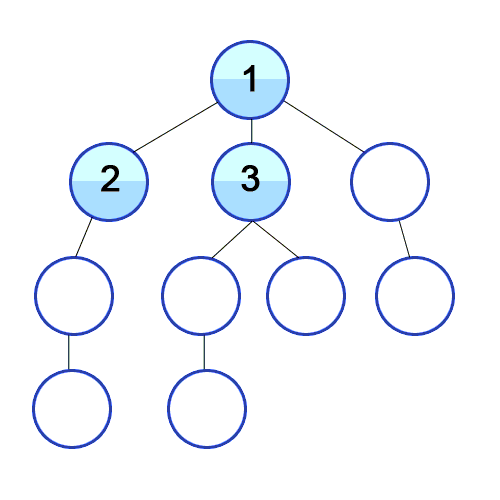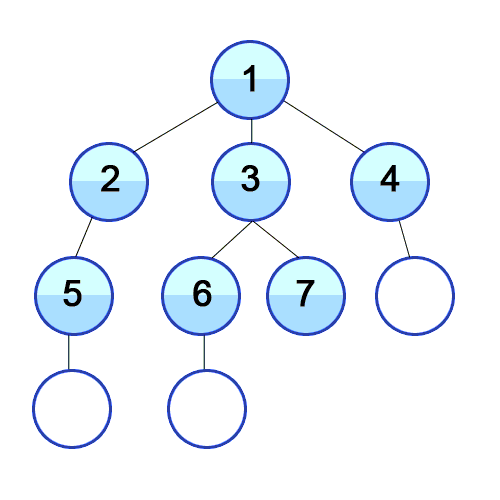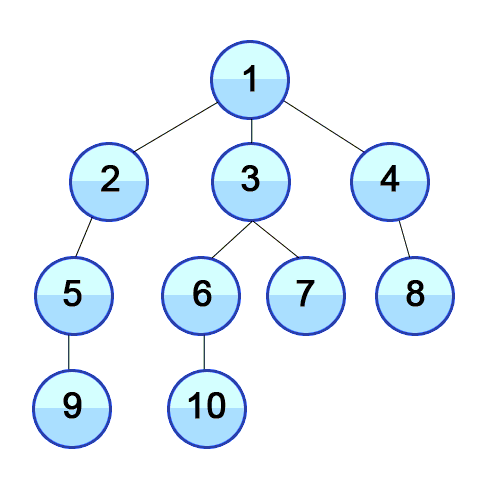
출처 : https://developer-mac.tistory.com/64

2-2. BFS Python 구현

from collections import deque

def bfs(v):
    # 큐 생성 및 큐에 시작 노드 삽입
    q = deque()
    q.append(v)
    
    # 아직 방문해야 하는 노드가 있다면
    while q:
        # 큐에서 노드를 꺼내서 x에 저장
        x = q.popleft()
        print(x, end=' ')
        
        # 그래프를 탐색하다가 방문하지 않은 노드가 있다면
        for i in graph[x]:
            if not visited[i]:
                # 큐에 방문하라고 삽입하고 방문 처리
                q.append(i)
                visited[i] = True

정리

DFS	BFS
현재 정점에서 갈 수 있는 점들까지 들어가며 탐색	현재 정점에 연결된 가까운 점들부터 탐색
Stack 또는 Recursive로 구현	Queue로 구현