
아래 백준 로고를 클릭하면 해당 문제로 이동합니다 😀
풀이과정
이 문제는 점과 점 사이의 거리를 생각해보면 쉽게 풀 수 있는 문제이다.
조건을 4가지 경우로 나누어 코드를 작성해야한다.
아래 나오는 그림에서 빨간원의 반지름을 r1, 파란원의 반지름을 r2라고 하자.
Case 1. 두 원이 일치하는 경우
이 경우, 두 원의 중점 좌표와 반지름의 길이가 동일해야한다.
dis 변수를 통해 두 좌표 사이의 거리를 구해놓았고, 이 거리를 이용하여 조건문을 작성한다.
두 원의 중점 좌표가 같다는 의미는 거리가 0이라는 의미이고, 반지름이 같다는 조건을 사용하면 된다.
Case 2. 두 원이 한 점에서 만나는 경우
외접 또는 내접을 의미한다.
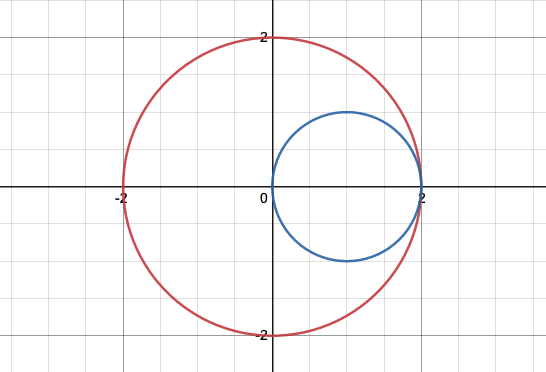
내접의 경우, 두 좌표 사이의 거리인 dis와 r2를 더한 값이 r1이 된다. 이를 일반화하면 r1-r2의 절댓값이 dis가 된다는 것이다.
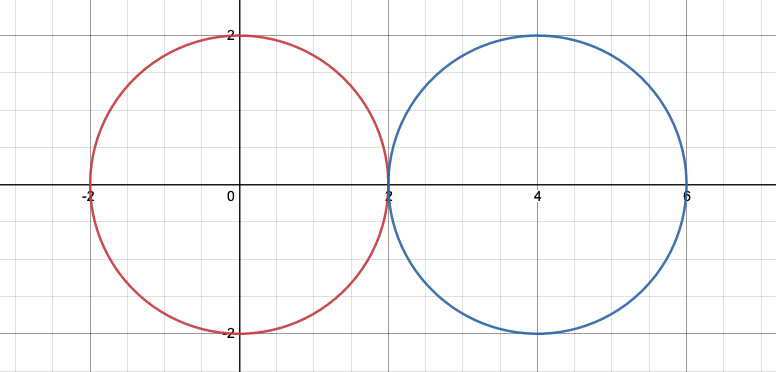
외접의 경우, 각각의 반지름인 r1과 r2의 합이 두 좌표 사이의 거리인 dis가 되어야한다.
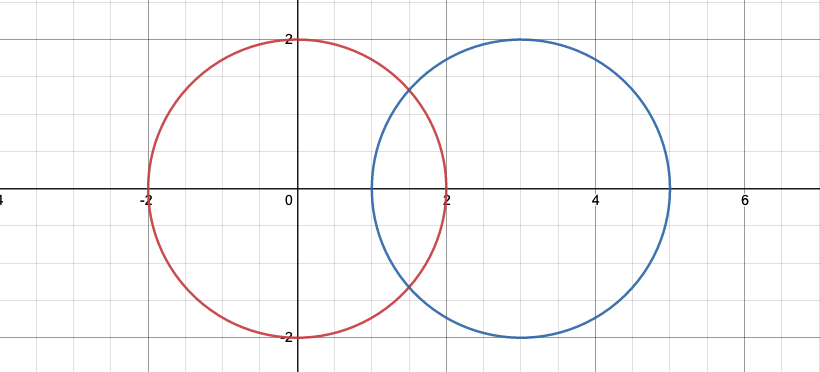
Case 3. 두 원이 두 점에서 만나는 경우
이 경우는 두 좌표 사이의 거리인 dis가 각각의 반지름의 차와 합 사이에 있어야한다.
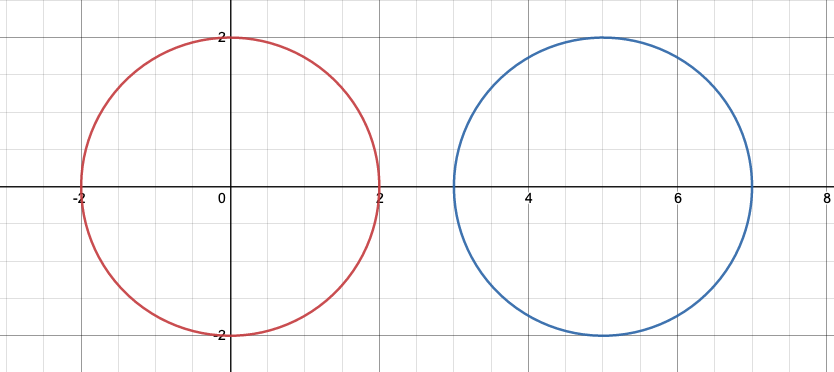
Case 4. 두 원이 만나지 않는 경우
위 조건에서 가능한 모든 조건을 걸었으므로 else구문으로 처리해주면 된다.
조건문을 걸자면, 두 좌표 사이의 거리인 dis가 각각의 반지름의 합보다 커야한다.
코드
구현은 다음과 같이 할 수 있다.
import math
T = int(input())
for i in range(T):
x1, y1, r1, x2, y2, r2 = map(int, input().split())
dis = math.sqrt((x1-x2)**2 + (y1-y2)**2)
# 두 원이 일치하는 경우
if dis == 0 and r1 == r2 :
print(-1)
# 두 원이 한 점에서 만나는 경우(외접 & 내접)
elif abs(r1 - r2) == dis or r1 + r2 == dis :
print(1)
# 두 원이 두 점에서 만나는 경우
elif abs(r1 - r2) < dis < (r1 + r2) :
print(2)
# 두 원이 만나지 않는 경우
else :
print(0)결과


