1️⃣ 복잡도

복잡도란 알고리즘의 성능, 효율성을 나타내는 척도이다.

크게, 시간 복잡도와 공간 복잡도로 나누어 볼 수 있다.

1. 시간 복잡도 Time Complexity

시간 복잡도란 특정 크기의 입력을 기준으로 할 때 필요한 연산의 횟수를 의미한다.

2. 공간 복잡도 Space Complexity

공간 복잡도란 알고리즘이 실행될 때 얼마나 많은 공간(메모리)가 필요한지를 의미한다.

3. 시간 복잡도 vs 공간 복잡도

시간 복잡도는 얼마나 빠르게 실행되는지, 공간 복잡도는 얼마나 많은 메모리가 필요한지를 판단한다.

시간 복잡도와 공간 복잡도는 반비례하는 경향이 있기 때문에, 알고리즘의 성능을 판단할 땐 시간 복잡도를 위주로 판단한다.

2️⃣ 빅오 Big-O Notation

• 복잡도를 나타내는 점근 표기법 중 가장 많이 사용되는 표기법
• 알고리즘 효율성을 상한선 기준으로 표기 → 즉, 알고리즘 최악의 경우를 고려하는데 가장 좋은 표기법

빅오메가는 하한선을 기준으로, 빅세타는 상한선과 하한선 사이를 기준으로 표기

1.  빅오 표기법 특징

1. 상수항, 계수 무시

   빅오 표기법은 n이 충분히 크다고 가정을 하고, 알고리즘의 효율성은 n의 크기에 영향을 받기 때문이다.

   → O(n+5)는 O(n)으로, O(2n)은 O(n)으로 간주한다.

2. 영향력 없는 항 무시

   빅오 표기법은 n의 크기에 영향을 받으므로 가장 영향력이 큰 항 이외에 영향력이 없는 항은 무시한다.

   → O($n^2 + 2n + 1$)은 O($n^2$)으로 간주한다.

2. 시간 복잡도 + 빅오 표기법

$O(1) < O(log n) < O(n) < O(n logn) < O(n^2) < O(2^n)$ < $O(n!)$

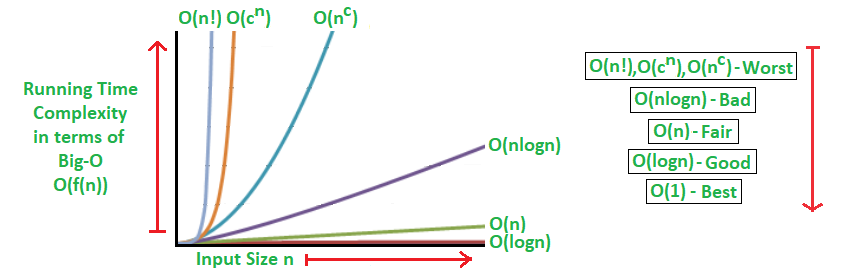
복잡도	소요 시간	예시
$O(1)$	상수 시간	스택에서 Push, Pop
$O(log n)$	로그 시간	이진 트리
$O(n)$	선형 시간	1중 for 문
$O(n log n)$	선형 로그 시간	퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap sort)
$O(n^2)$	2차 시간	이중 for 문, 삽입 정렬(insertion sort), 거품 정렬(bubble sort), 선택 정렬(selection sort)
$O(C^n)$	지수 시간	피보나치 수열
$O(n!)$	팩토리얼 시간	순열(permutation), 조합(combination)

2-1. O(1): 상수 시간 복잡도

입력값(n)이 증가하더라도 실행시간은 변하지 않는 알고리즘

입력값의 크기와 관계없이 즉시 출력값을 얻을 수 있다.

const sum = (n+1) * n /2;

2-2. O($logn$): 로그 시간 복잡도

입력값의 크기가 커질수록 실행 시간이 로그(지수 함수의 역함수)만큼 짧아지는 알고리즘

function printNum(n){
	let i = 1;
	while(i < n){
		console.log(i);
		i = i*2;
	}
}

2-3. O($n$): 선형 시간 복잡도

입력값의 증가도에 따라 시간도 동일한 비율로 증가하는 알고리즘

let sum = 0;
for(let i = 0 ; i <= n ; i++){
	sum += i;
}

2-4. O($nlogn$): 선형 로그 시간 복잡도

O(n) 알고리즘과 O(logn)의 알고리즘이 중첩된 것이다.

데이터가 많아질수록 성능이 향상되고, 거의 모든 정렬 알고리즘이 이 복잡도이다.

// 고기 순서대로 정렬하는 코드
function sortMeats(meats) {
  if (meats.length <= 1) {
    return meats; // 고기 1개만 있으면 바로 리턴
  }

  const mid = Math.floor(meats.length / 2); // 고기를 반으로 자름
  
  // 여기서 왼쪽 고기와 오른쪽 고기를 재귀 함수로 계속 쪼갬
  // 더 이상 쪼갤 수 없을 때 (1개 남을 때) 쪼개기를 멈춤
  const left = sortMeats(meats.slice(0, mid)); // 왼쪽 고기 정렬
  const right = sortMeats(meats.slice(mid)); // 오른쪽 고기 정렬

  return merge(left, right); // 이제 두 조각을 비교하면서 다시 합침
}

function merge(left, right) {
  let result = [];
  let i = 0;
  let j = 0;

  // 양쪽 고기를 비교해서 순서대로 합쳐줌
  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) {
      result.push(left[i]);
      i++;
    } else {
      result.push(right[j]);
      j++;
    }
  }

  // 남은 고기들 다 넣어줌
  return result.concat(left.slice(i)).concat(right.slice(j));
}

// 👉 쪼개는 데 걸리는 시간 → O(log n)
// 👉 합치는 데 걸리는 시간 → O(n)
// => O(n log n)

2-5. O($n^2$): 2차 시간 복잡도

입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 알고리즘

function printNum(n){
	for(let i = 0 ; i <= n ; i++){
		for(let j = 0 ; j <= n ; j++){
			console.log(i, j);
		}
	}
}

2-6. O($2^n$): 지수 시간 복잡도

주로 재귀적으로 수행하는 알고리즘으로, 모든 경우의 수를 탐색할 때 나온다.

function fibonacci(n){
	if(n <= 1) return n;
	return fibonacci(n-1) + fibonacci(n-2);
}

2-7. O($n!$): 팩토리얼 시간 복잡도

순열, 조합 알고리즘에서 나온다.

function arrangeCars(cars) {
  if (cars.length === 0) {
    return [[]]; // 아무 차도 없으면 빈 배열 하나 리턴
  }

  let result = [];
  for (let i = 0; i < cars.length; i++) {
    let remaining = cars.slice(0, i).concat(cars.slice(i + 1)); // i번째 차를 뺌
    let perms = arrangeCars(remaining); // 나머지 차들 순서를 구함

    for (let perm of perms) {
      result.push([cars[i], ...perm]); // i번째 차 + 나머지 차들 조합
    }
  }
  return result;
}

3. 공간복잡도 + 빅오 표기법

알고리즘 실행에 메모리가 얼마나 사용되는지를 계산하면 된다.