완전탐색은 탐색 알고리즘의 한 종류로, 가능한 모든 경우의 수를 탐색하여 정답을 찾아내는 방법입니다.
가능한 모든 경우를 하나씩 대입하여 확인하는 방식이므로, "무식하게(brute force)" 푸는 방법이라고도 불립니다.
보통 알고리즘은 최대한 빠르게 정답을 찾아내는 것이 중요하지만, 완전탐색은 모든 경우를 전부 계산하기 때문에
효율적인 알고리즘이라고 하기엔 다소 어려움이 있습니다.
하지만 최적의 해를 반드시 보장하기 때문에, 경우의 수가 적을 때는 충분히 사용할 수 있는 방법입니다.
🔍 완전탐색 알고리즘의 종류
완전탐색에는 여러 가지 방법이 있으며, 대표적으로 다음과 같은 알고리즘이 있습니다.
- Brute Force
- 재귀 (Recursion)
- 비트마스크 (Bitmasking)
- 순열 (Permutation)
- 백트래킹 (Backtracking)
- 비 선형구조 탐색 : DFS / BFS (다음 포스팅에서 다룰 예정)
이제 하나씩 살펴보겠습니다.
1. Brute Force
가장 기본적인 완전탐색 방법으로, for문, while문, if문 등을 이용하여 모든 경우를 전부 탐색하는 방식입니다.
무식하지만 확실하게 답을 찾을 수 있으며, 경우의 수가 적을 때 사용할 수 있습니다.
✅ 예제: 배열에서 특정 숫자 찾기
const arr = [1, 2, 3, 4, 5];
const target = 3;
for (let i = 0; i < arr.length; i++) {
if (arr[i] === target) {
console.log(`정답 : ${arr[i]}`);
}
}위 코드에서는 배열을 처음부터 끝까지 전부 확인하면서 target 값을 찾고 있습니다.
이처럼 모든 경우를 하나씩 확인하는 것이 Brute Force 방식입니다.
📌 Brute Force의 시간 복잡도
위 예제에서는 단순히 for문을 한 번만 실행하고, target 값을 찾는 순간 종료할 수도 있습니다.
하지만 일반적으로 모든 경우를 탐색해야 한다는 점에서 Brute Force의 시간 복잡도는 다음과 같이 계산됩니다.
1 단순 탐색의 경우
- 배열의 크기가
N일 때, 최악의 경우N번 반복해야 함. - 즉, 시간 복잡도는 O(N).
2 중첩 반복문을 사용하는 경우
- Brute Force는 경우의 수를 모두 시도하기 때문에, 중첩된
for문이 있을 경우 O(N²) 이상의 시간 복잡도가 발생할 수 있습니다.
const arr = [1, 2, 3, 4, 5];
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length; j++) {
console.log(arr[i], arr[j]); // 모든 경우의 수 탐색
}
}📌 이 경우 시간 복잡도는 O(N²) → 입력 크기가 커질수록 연산량이 기하급수적으로 증가합니다.
즉, Brute Force 방식은 단순한 문제에서는 효과적이지만, 경우의 수가 많아질수록 비효율적일 수 있습니다.
2. 재귀 함수 (Recursion)
재귀 함수는 문제를 작은 단위로 쪼개어 해결하는 방법입니다.
특정 조건을 만족하면 자기 자신을 계속 호출하는 방식으로 동작합니다.
✅ 예제: 1부터 N까지 출력하는 재귀 함수
function printNumbers(n) {
if (n === 0) return; // 종료 조건
printNumbers(n - 1);
console.log(n);
}
printNumbers(5);위 코드는 printNumbers(5)를 호출하면, 5 → 4 → 3 → 2 → 1 순서로 재귀 호출이 이루어집니다.
재귀를 활용하면 완전탐색을 더 효율적으로 구현할 수 있습니다.
📌 재귀 함수의 시간 복잡도
위 예제의 printNumbers(n) 함수는 재귀적으로 호출되며, n에서 0까지 감소하는 방식입니다.
function printNumbers(n) {
if (n === 0) return; // 종료 조건
printNumbers(n - 1); // 재귀 호출
console.log(n); // 출력
}
printNumbers(5);✅ 호출 과정 (printNumbers(5))
printNumbers(5) → printNumbers(4)
→ printNumbers(3) → printNumbers(2)
→ printNumbers(1) → printNumbers(0) (종료)➡ 총 n + 1번 호출됨 (n부터 0까지)
✅ 시간 복잡도 계산
- 함수가 한 번 호출될 때마다
printNumbers(n - 1)을 한 번만 호출 합니다. 즉, 호출 횟수는n번이며, 각 호출에서 O(1)의 연산이 수행됩니다. 따라서 총 시간 복잡도는O(n)
만약, 재귀 함수가 여러 번 호출되는 경우, 시간 복잡도가 증가할 수 있습니다.
✅ 예제: 피보나치 수열 (Fibonacci Sequence)
function fibonacci(n) {
if (n <= 1) return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}
console.log(fibonacci(5));
✅ 호출 과정 (fibonacci(5))
fibonacci(5) → fibonacci(4) + fibonacci(3)
→ (fibonacci(3) + fibonacci(2)) + (fibonacci(2) + fibonacci(1))
→ ...➡ 한 번의 호출에서 두 번의 재귀 호출이 발생하기 때문에, 트리 형태의 호출 구조가 생기며, 총 호출 횟수는 `O(2^n)이 됩니다.
3. 비트마스크 (Bitmasking)
비트 연산자 (|, &, << 등)를 활용해 문제를 해결하는 방식으로, 부분 집합을 구하거나 특정 조건을 빠르게 체크할 때 유용합니다.
✅ 비트 연산자 (Bitwise Operators)
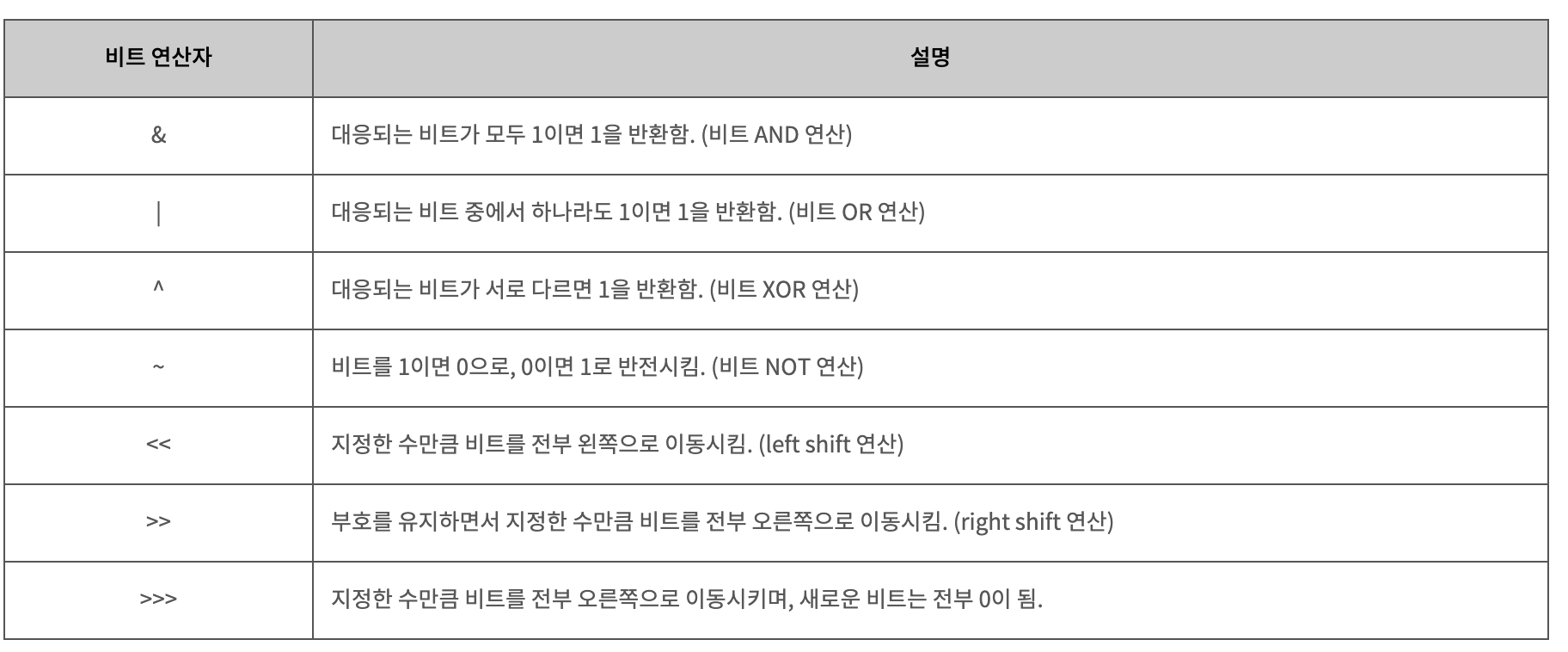
✅ 비트마스크 활용 예제: 부분 집합 구하기
const arr = [1, 2, 3];
const n = arr.length;
for (let i = 0; i < (1 << n); i++) { // 2^n 개의 부분집합 탐색
let subset = [];
for (let j = 0; j < n; j++) {
if (i & (1 << j)) subset.push(arr[j]); // j번째 비트가 1이면 해당 원소 포함
}
console.log(subset);
}✅ 시간 복잡도 O(2^N), 연산 속도가 빠름
✅ (1 << j)를 사용하여 특정 비트가 포한되어 있는지 확인
전에 백엔드 개발자분께서 권한 관리를 비트로 한다고 했을 때, 당시에는 이해가 안 갔지만, 공부하면서 비트마스크를 활용하면 메모리를 절약하고 연산을 빠르게 수행할 수 있다는 점을 조금은 이해할 수 있었습니다..
사실 아직도, 굳이 이걸 써야 하나? 싶긴 하지만, 메모리 관리가 중요한 시스템에서는 유용하게 쓰일 것 같긴합니다.
예를 들어, 권한을 관리하거나, 대량의 데이터를 효율적으로 저장할 때는 꽤 효과적인 방식이라는 점이라고 생각합니다.
다만, 프론트엔드 개발에서는 비트마스크를 사용할 일이 거의 없을 것 같다는 생각이 듭니다.
오히려 비트 연산을 쓰면 코드가 난독화되어 다른 프론트엔드 개발자가 읽기 어려운 코드가 될 가능성이 높다고 판단됩니다.
프론트엔드에서는 가독성이 더 중요한 경우가 많으니, 굳이 비트 연산을 사용할 필요는 없지 않을까? 하는 생각이 듭니다.
4. 순열 (Permutation)
순열이란 주어진 숫자들을 배치할 수 있는 모든 경우를 의미합니다.
즉, 숫자의 순서가 다르면 서로 다른 경우로 취급합니다.
예를 들어, [1, 2, 3]의 경우
[1, 2, 3]과[3, 2, 1]은 서로 다른 경우로 인정됩니다.
즉, 순열을 구한다는 것은 모든 가능한 배치를 나열하는 것을 의미합니다.
✅ 순열을 구하는 사고 과정
순열을 구하는 과정은 재귀적(Recursive) 사고 방식을 사용합니다.
📌 1. 숫자가 한 개일 때
[1] // 그 자체가 순열이 됩니다. (1)📌 2. 숫자가 두 개일 때
[1, 2] → [1, 2], [2, 1]📌 3. 숫자가 세 개일 때 ([1, 2, 3])
각 숫자를 처음에 놓고, 나머지 숫자로 다시 순열을 만듭니다.
1을 첫 번째 자리에 놓고[2, 3]의 순열을 구함2를 첫 번째 자리에 놓고[1, 3]의 순열을 구함3을 첫 번째 자리에 놓고[1, 2]의 순열을 구함
1️⃣ [1] + 순열([2, 3]) → [1, 2, 3], [1, 3, 2]
2️⃣ [2] + 순열([1, 3]) → [2, 1, 3], [2, 3, 1]
3️⃣ [3] + 순열([1, 2]) → [3, 1, 2], [3, 2, 1]➡ 모든 경우의 수를 나열하면 다음과 같습니다.
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]이 과정을 반복하면 어떤 숫자가 주어지더라도 순열을 구할 수 있습니다!
✅ 순열을 구하는 코드
위의 개념을 재귀(Recursive Function) 를 이용해 코드로 표현하면 아래와 같습니다.
function permute(arr, selected = []) {
if (arr.length === 0) {
console.log(selected); // 모든 숫자를 선택한 경우 출력
return;
}
for (let i = 0; i < arr.length; i++) {
let newArr = [...arr]; // 배열 복사
newArr.splice(i, 1); // 현재 선택한 숫자 제외
permute(newArr, [...selected, arr[i]]); // 선택한 숫자를 추가하여 재귀 호출
}
}
permute([1, 2, 3]);- 처음 숫자를 선택하고, 나머지 숫자로 순열을 구하는 방식
- 배열이 비어있으면 하나의 순열을 완성한 것이므로 출력
📌 다음 순열(Next Permutation) 문제 해결 방법
만약 다음 순열을 구하는 문제가 주어진다면, 다음과 같은 공식으로 풀 수 있습니다.
예를 들어, 다음과 같은 배열이 주어졌다고 가정해 본다면,
let arr = [1, 2, 3, 6, 5, 4];이 배열의 다음 순열을 구하는 공식적인 방법은 다음과 같습니다.
✅ 다음 순열을 구하는 공식적인 방법
-
배열을 뒤에서부터 탐색하며 가장 긴 '내림차순'을 찾는다.
- 즉, 처음으로 증가하는 위치를 찾는다.
- 이 위치가 순열을 변경할 기준점이 됨.
-
그 위치의 값보다 큰 값 중, 가장 오른쪽에 있는 작은 값과 Swap(교환)
- 사전순으로 다음 순열을 만들기 위해, 가장 작은 증가 요소를 찾아 교환.
-
기준점 이후의 숫자들을 '오름차순' 정렬
- Swap 후에는 뒷부분을 오름차순 정렬하여 사전순으로 다음에 오는 순열을 만든다.
function nextPermutation(arr) {
let i = arr.length - 2;
// 1. 뒤에서부터 탐색하며 증가하는 지점 찾기
while (i >= 0 && arr[i] >= arr[i + 1]) {
i--;
}
if (i >= 0) {
let j = arr.length - 1;
// 2. arr[i]보다 크면서 가장 작은 값을 찾기
while (arr[j] <= arr[i]) {
j--;
}
// 3. Swap (값 교환)
[arr[i], arr[j]] = [arr[j], arr[i]];
}
// 4. i 이후의 숫자들을 오름차순 정렬
let left = i + 1, right = arr.length - 1;
while (left < right) {
[arr[left], arr[right]] = [arr[right], arr[left]];
left++;
right--;
}
}
let arr = [1, 2, 3, 6, 5, 4];
nextPermutation(arr);
console.log(arr); // [1, 2, 4, 3, 5, 6]순열의 경우 모든 숫자를 배치하는 방법을 고려해야 하므로 N!(팩토리얼) 개의 경우가 존재합니다. 즉, 시간 복잡도는 O(N!) 이 됩니다. 그렇기 때문에, N이 커질수록 계산량이 급격히 증가하므로 최적화 필요할듯합니다.
5. 백트래킹 (Backtracking)
백트래킹(Backtracking)은 가능성이 없는 경로는 미리 탐색을 중단하는 방식입니다.
즉, "가망이 없는 경우는 빨리 포기하고 되돌아간다(Backtrack)"는 원리로 동작합니다.
완전 탐색(Brute Force)보다 더 효율적인 탐색 방법으로 사용됩니다.
백트래킹이 중요한 이유
1. 모든 경우의 수를 탐색해야 하지만, 불필요한 탐색은 줄이고 싶을 때
2. 가능한 해를 찾는 문제에서 효율적인 탐색이 필요할 때 즉, 불필요한 탐색을 줄일때
백트래킹 문제를 풀 때 가장 중요한 개념은 다음 두 가지입니다.
Pruning (가지치기)
- 불필요한 경로를 미리 제거하여 탐색을 줄이는 기법
- 즉, 가능성이 없는 경로라면 더 깊이 탐색하지 않고 되돌아가는 것
재귀적 탐색 + 원상복구
- 백트래킹을 진행하면서, 탐색했던 값을 재귀적으로 처리한 후 원상복구하는 과정이 필수
백트래킹 예제: N-Queen 문제
백트래킹을 설명할때, 가장 많이 나오는 예제는 N-Queen 인듯 합니다. 이 문제로, 백트래킹을 어떻게 구현할 수 있는지 설명해보겠습니다.
N-Queen 문제는 N x N 체스판에 N개의 퀸을 서로 공격하지 않도록 배치하는 문제입니다.
퀸은 같은 행, 같은 열, 그리고 대각선 방향으로 이동할 수 있기 때문에
백트래킹을 활용하여 탐색을 줄이는 것이 중요합니다.
해결 방법
- 퀸을 한 줄씩 배치하면서 조건을 만족하는지 체크
- 이미 공격받는 위치라면 더 이상 탐색하지 않음 (Pruning)
- 모든 퀸을 배치하면 정답으로 저장
- 재귀적으로 탐색하며, 원상복구하여 다른 경우도 탐색
function solveNQueen(N) {
let board = new Array(N).fill(-1);
let result = [];
function backtrack(row) {
if (row === N) {
result.push([...board]); // 하나의 해를 저장
return;
}
for (let col = 0; col < N; col++) {
if (isValid(board, row, col)) {
board[row] = col; // 🔹 현재 행(row)에 퀸 배치
backtrack(row + 1); // 🔹 다음 행 탐색 (재귀 호출)
board[row] = -1; // 🔹 원상복구 (다른 경우 탐색을 위해)
}
}
}
function isValid(board, row, col) {
for (let i = 0; i < row; i++) {
if (board[i] === col || Math.abs(board[i] - col) === Math.abs(i - row)) {
return false;
}
}
return true;
}
backtrack(0);
console.log(result);
}
solveNQueen(4);✅ 불필요한 탐색을 피하기 위해 isValid() 함수로 Pruning 적용
✅ 재귀적으로 탐색을 진행하면서 유효한 경우에만 진행
✅ 탐색이 끝나면 원상복구(board[row] = -1)하여 다른 경우도 탐색 가능하게 함
백트래킹 문제를 만났을때, 다음과 같은 사고과정을 통하면 어떻게 문제를 풀지 좀 더 감이 잡히는듯 합니다.
- 문제를 보고 "모든 경우의 수"를 탐색해야 한다면, 백트래킹을 고려합니다.
- 탐색 중 불필요한 경우를 빨리 포기하는 "Pruning"을 적용 즉, 재귀 탈출 조건을 고려합니다.
- 현재 상태를 저장하거나 원상복구하여 다른 경우를 탐색할 준비
📌 마무리
완전탐색(Brute Force)은 모든 경우의 수를 탐색하여 해를 구하는 방식입니다.
하지만 경우의 수가 많아지면 시간이 오래 걸리므로,
👉 백트래킹 등의 기법을 활용하여 최적화하는 것이 중요합니다!
다음 포스팅에서는 DFS와 BFS를 활용한 탐색 기법에 대해 다뤄보겠습니다. 🚀
완전탐색 알고리즘 팁
완전탐색 알고리즘 부터 난이도가 확 올리가, 이해하는데 어려움을 많이 겪었는데, Chat-gpt와 다음과 같이 공부하면서 이해도를 높였습니다. 저처럼 공부해보시면 좋을것같습니다!