1. 7장 읽기
2. 연습문제 14 풀기
14. Show that the time complexity for the number of assignments of records for the Mergesort algorithm (Algorithms 2.2 and 2.4) is approximated by T (n) = 2n lg n.
Mergesort 알고리즘은 입력 배열을 두 개의 작은 배열로 나누고, 각각을 재귀적으로 정렬 한 다음 두 개의 정렬 된 배열을 병합하여 최종 정렬 된 배열을 얻는다. 이 알고리즘에서 레코드 할당 횟수는 두 가지 종류이다.
- 원래 배열을 분할하여 작은 배열로 복사하는 데 필요한 할당
- 두 개의 작은 배열을 병합하여 정렬 된 배열을 만드는 데 필요한 할당
첫 번째 종류의 할당은 배열의 크기와 상관없이 항상 1회 발생한다.
두 번째 종류의 할당은 배열의 크기와 병합하는 방법에 따라 달라진다. Mergesort 알고리즘에서는 일반적으로 Bottom-up mergesort 와 Top-down mergesort 두 가지 방법으로 구현됩니다.
Bottom-up mergesort 에서는 각 단계에서 두 개의 작은 배열을 병합하므로 레코드 할당 횟수는 최대 n 번이다. 이 알고리즘에서는 배열을 2배씩 병합하므로, 전체 병합 단계 수는 lg n이다. 따라서 두 번째 종류의 할당은 대략 2n lg n회 발생한다.
Top-down mergesort 에서는 재귀 호출에 따라 두 개의 작은 배열을 병합한다. 각 재귀 호출에서는 최대 n번의 할당이 필요하며, 전체 재귀 호출 수는 lg n이다. 따라서 두 번째 종류의 할당은 대략 2n lg n회 발생한다.
따라서 Mergesort 알고리즘의 시간 복잡도는 T(n) = 2n lg n으로 근사한 값이 된다.
3.
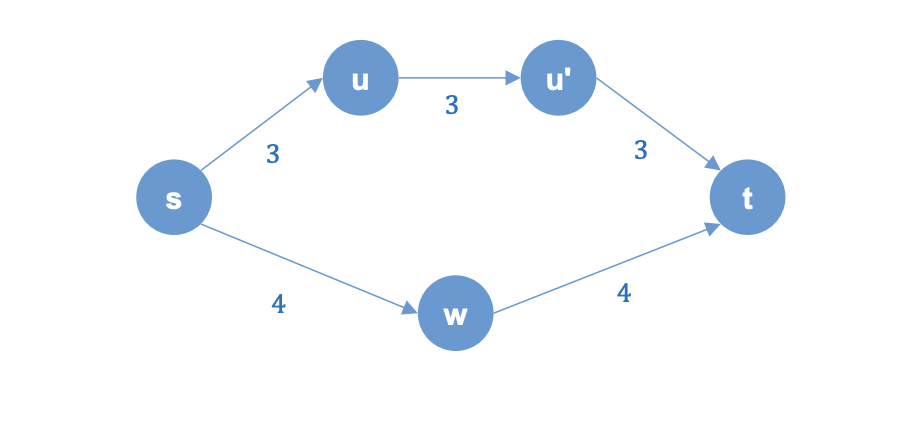
3번, 4번은 잘 모르겠습니다..
