그래프는 현상이나 사물을 정점과 간선으로 표현하는것으로, 점정(Vertex)은 대상이나 개체를 나타내고 간선(Edge)은 이들 간의 관계를 나타낸다.
먼저 그래프의 표현을 살펴보도록 하겠다. 그래프의 표현에는 두가지 방법을 살펴보도록 하겠다. 인접 행렬 방식과 인접 리스트 방식이 존재한다.
인접 행렬
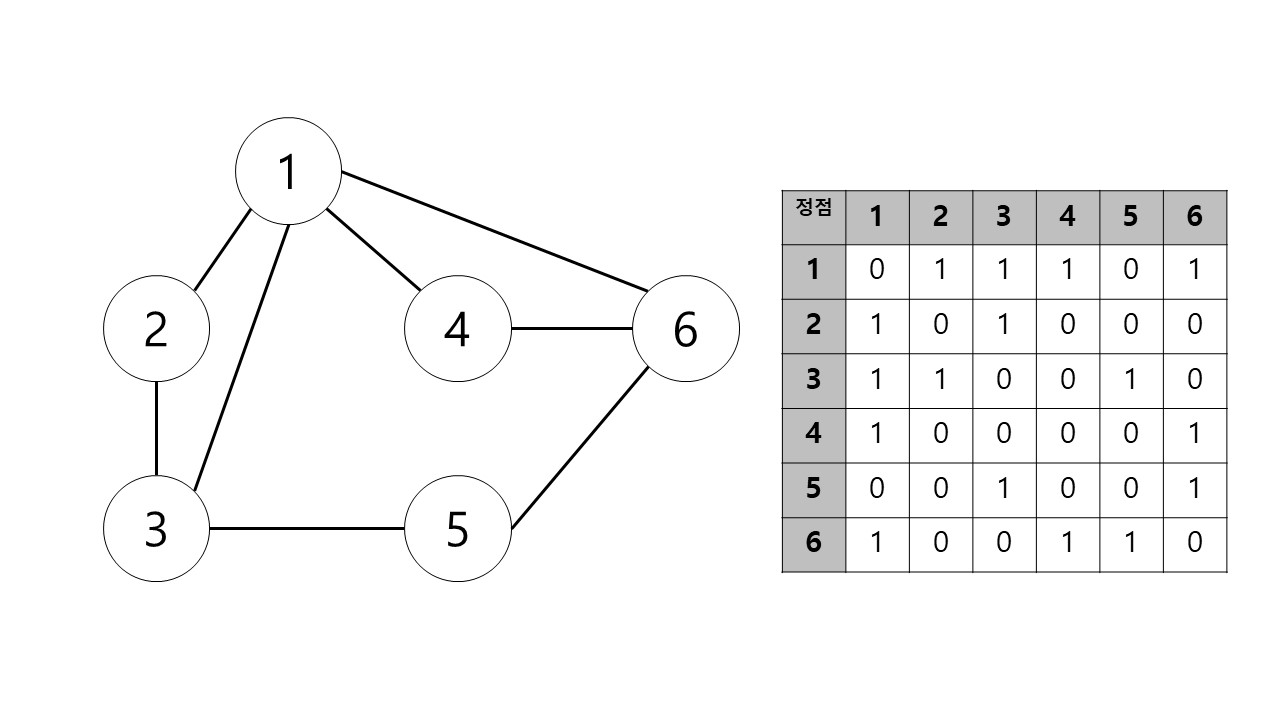
그래프 G = (V, E)에서 정점의 총수가 N이라고 하자, 우선 N x N 행렬을 준비한다. 정점 i와 j간에 간선이 있으면 행렬의 (i,j) 원소와 (j,i)원소의 값을 1로 할당한다. 간선으로 연결된 두 정점은 인접하다(Adhacent)고 한다.
지금 설명한 그래프는 무향 그래프로 간선이 연결된 양쪽 정점에는 간선이 존재하는 형태이다. 하지만 유향 그래프의 경우 한쪽 방향으로만 연결이 될 수도 있다.
예를들어 i에서 j로는 간선이 있지만 j에서 i에는 간선이 없는 경우이다. 이럴경우에는 행렬의 (i,j)원소의 값을 1로 할당하지만 (j,i)원소의 값은 0으로 할당한다.
무향 그래프
유향 그래프
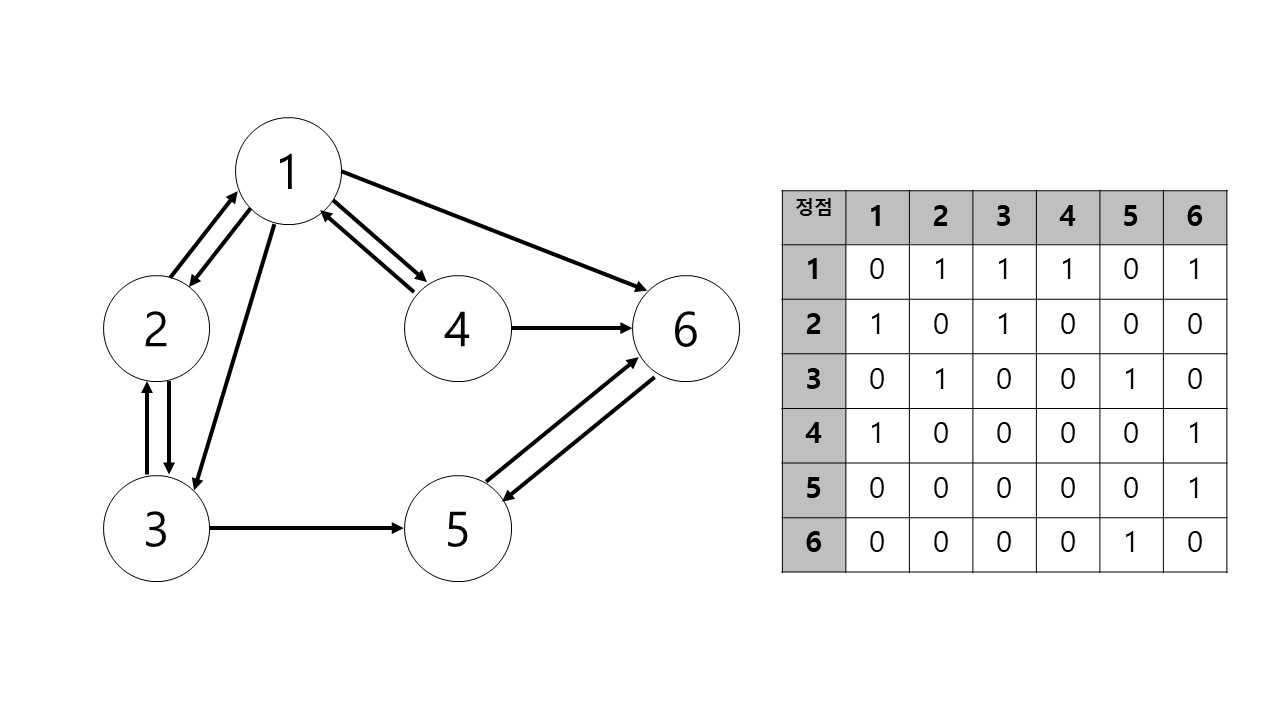
사진과 동일하게 무향 그래프와 유향 그래프를 그릴 수 있다.
가중치가 있는 그래프
그래프에는 가중치가 존재할수도있다. 가중치란 간선을따라 이동하는데 필요한 비용이라고 생각하면 편하다. 가중치가 존재할때는, 인접행렬에 0과 1이 아닌 0과 가중치로 표현하면 된다. 만약 행렬의 값이 0이라면 간선이 없는것이고, 행렬의값이 0이 아닌 자연수라면 그만큼의 가중치가 필요한 간선이 존재한다는 의미이다.
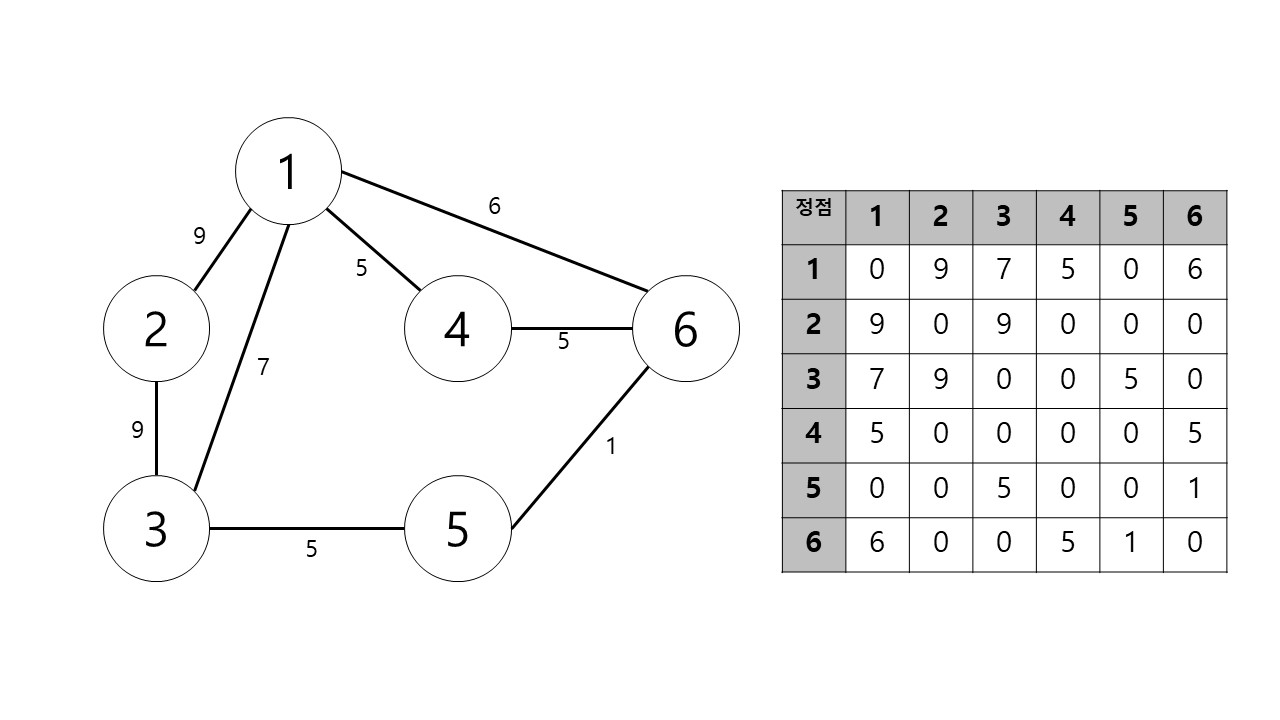
행렬 표현법은 이해하기 쉽고 간선의 존재 여부를 즉각 알 수 있다는 장점이 있다. 정점 i와 정점 j의 인접 여부는 행렬의 (i,j)원소나 (j,i)원소의 값만 보면 알 수 있다.
대신 인접 행렬 방식은 N x N 행렬이 필요하므로 N^2에 비례하는 공간이 필요하고, 행렬의 준비 과정에서 행렬의 모든 원소를 채우는 데만 N^2에 비례하는 시간이 든다. 그러므로 O(N^2)미만의 시간이 소요되는 알고리즘이 필요한 경우에 행렬 표현법은 적절하지 않다.
인접 리스트
인접 리스트 표현법은 각 정점에 인접한 정점들을 리스트로 표현하는 방법이다. 각 정점마다 리스트를 하나씩 만든다. 여기에 각 정점에 인접한 정점들을 연결 리스트로 매단다.
인접 리스트 표현에서는 행렬 표현과 달리 존재하지 않는 간선은 표현상에 나타나지 않는다. 인접리스트는 공간이 간선의 총수에 비례하는 양만큼 필요하므로 대체로 행렬 표현에 비해 공간의 낭비가 없다.
모든 가능한 정점 쌍에 비해 간선의 수가 적을 떄 특히 유용하다. 그렇지만 거의 모든 정점 쌍에 대한 간선이 존재하는 경우에는 오히려 리스트를 만드는 데 필요한 오버헤드만 더 든다.
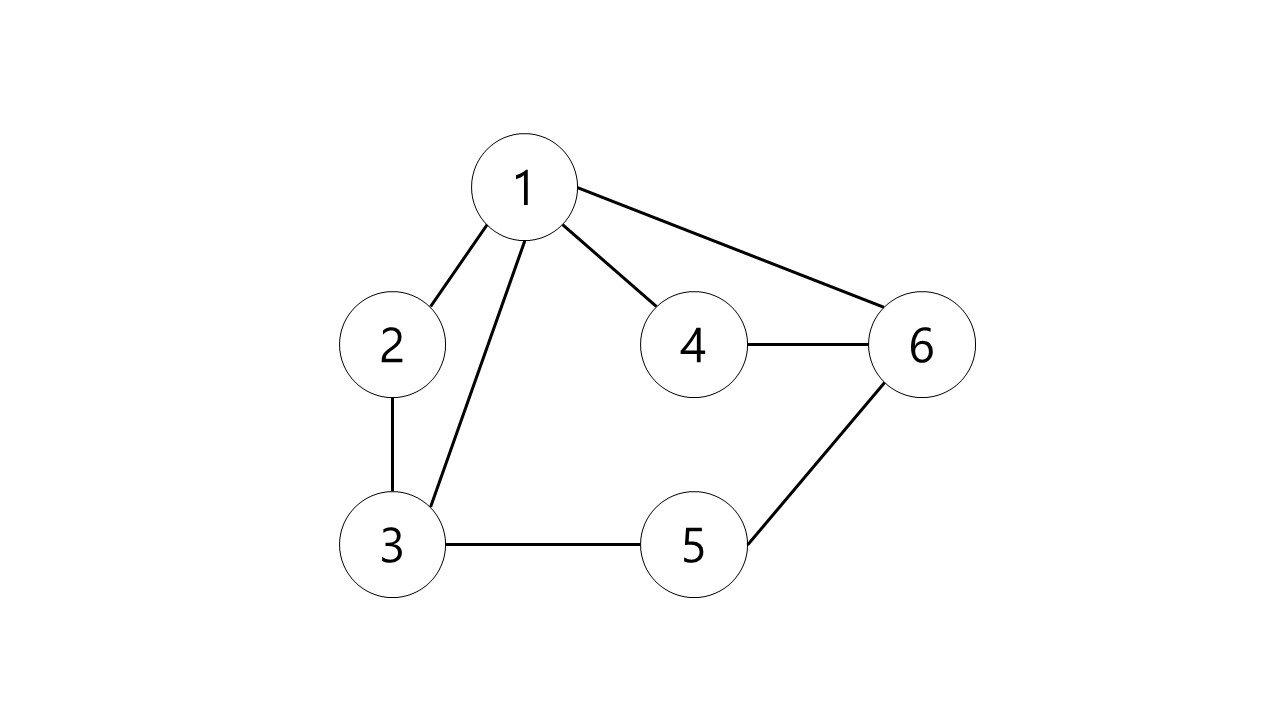
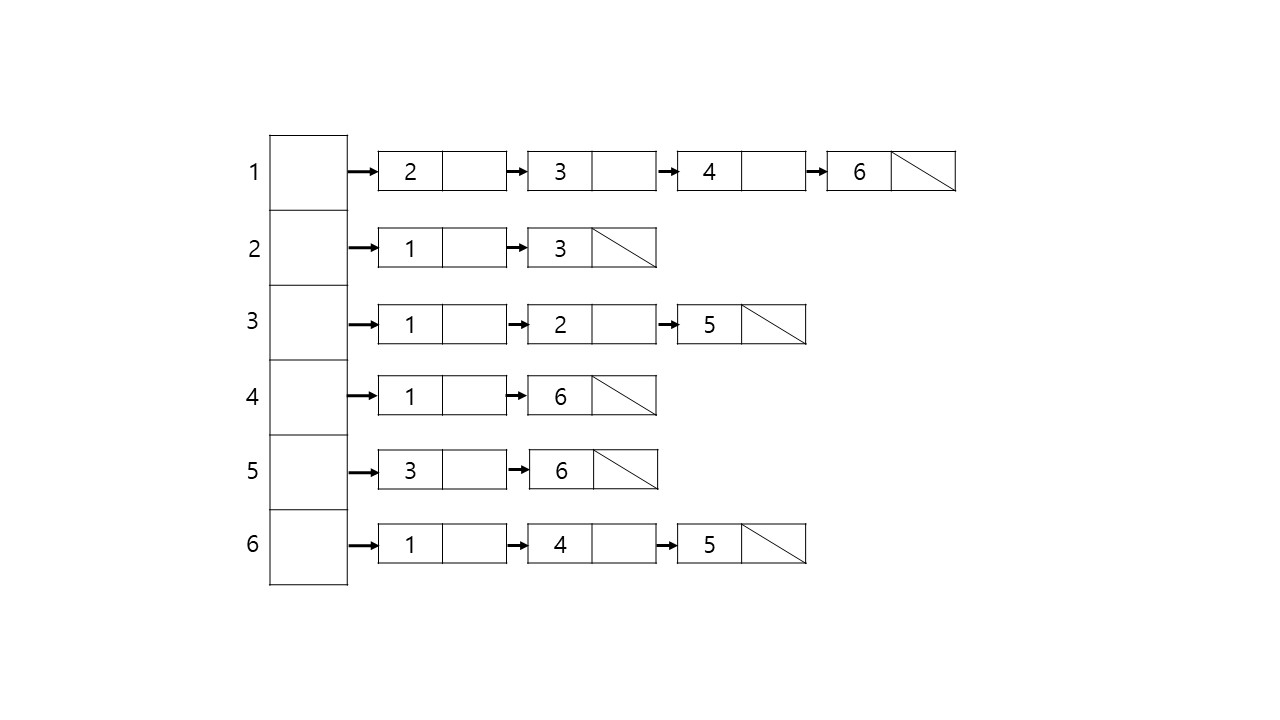
무향 그래프의 경우 하나의 간선에 두방향 모두 저장해야한다. 예를들어 (1, 3)이라는 간선이 존재한다면 1번에 3번을 추가해주고 3번에도 1번을 추가해야한다.
가중치가 있는 그래프
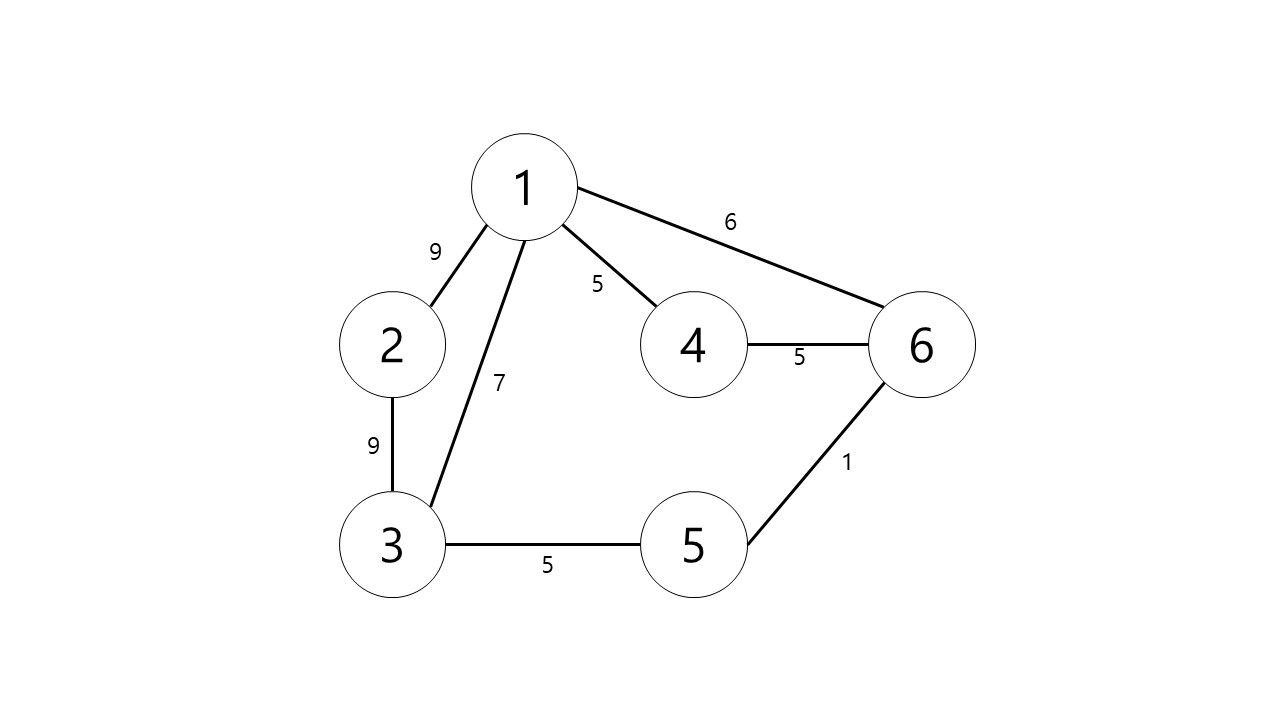
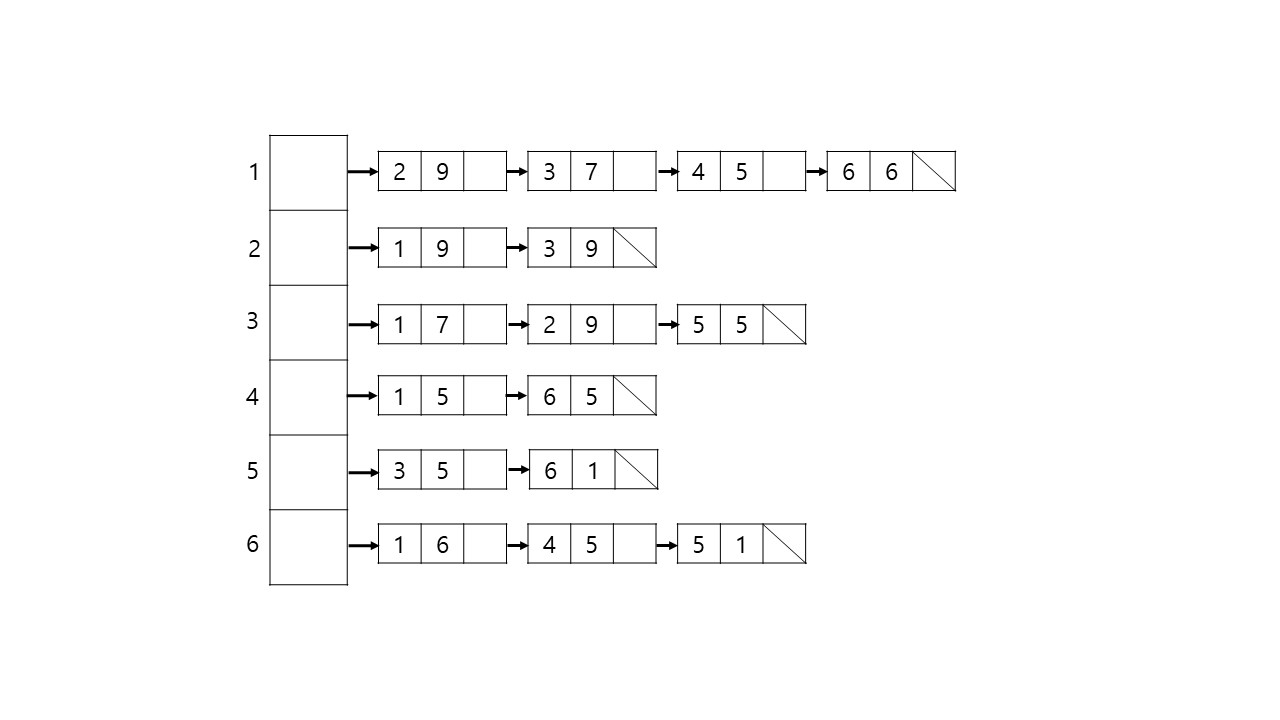
가중치가 있는 그래프는 이렇게 2차원 배열을 저장하게된다. C언어에서는 구조체를 만들어 노드 번호, 간선의 가중치, 연결된 다음 노드를 저장하지만, java를 예로들면 이중 리스트를 만들어 단일 리스트를 추가해주면된다.
DFS와 BFS
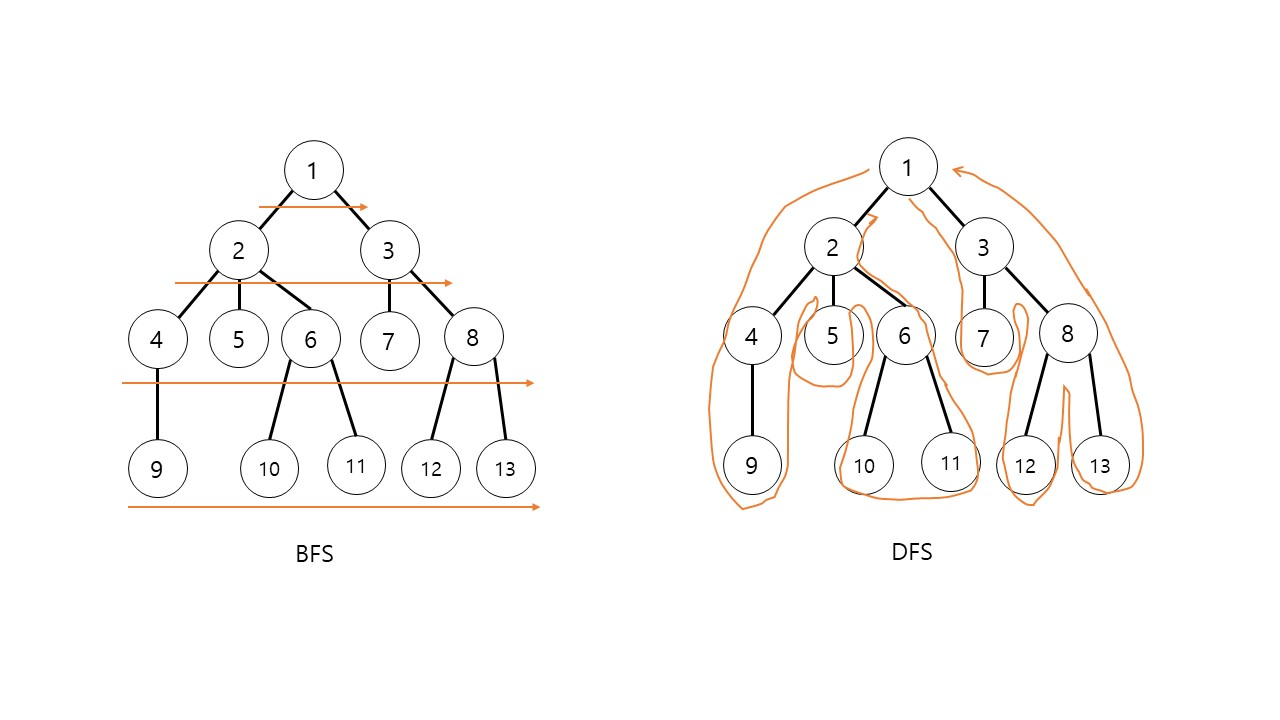
너비우선탐색과 깊이우선탐색을 그린 사진이다. 일반적으로 그래프를 대상으로 하는 두 탐색에 대한 설명에 앞서 직관적인 이해를 돕기 위해 트리를 대상으로 그림을 그려본 것이다.
너비우선탐색(BFS, Breadth-First Search)는 루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법이다. 즉, 먼저 루트의 자식을 차례로 방문한다. 다음으로 루트 자식의 자식을 방문하는식으로 방문한다 말그대로 정말 양옆으로 먼저 탐색하는 방법이다. 너비우선탐색은 큐를 사용한다.
깊이우선탐색(DFS, Deapth-First Search)는 자식 정점을 하나 방문한 다음 아래로 내려갈 수 있는 곳까지 내려간다. 더 이상 내려갈 수가 없으면 위로 되돌아오다가 내려갈 곳이 생기만 즉각 내려간다. 깊이우선탐색은 재귀와 스택을 사용한다.
BFS(너비우선탐색)
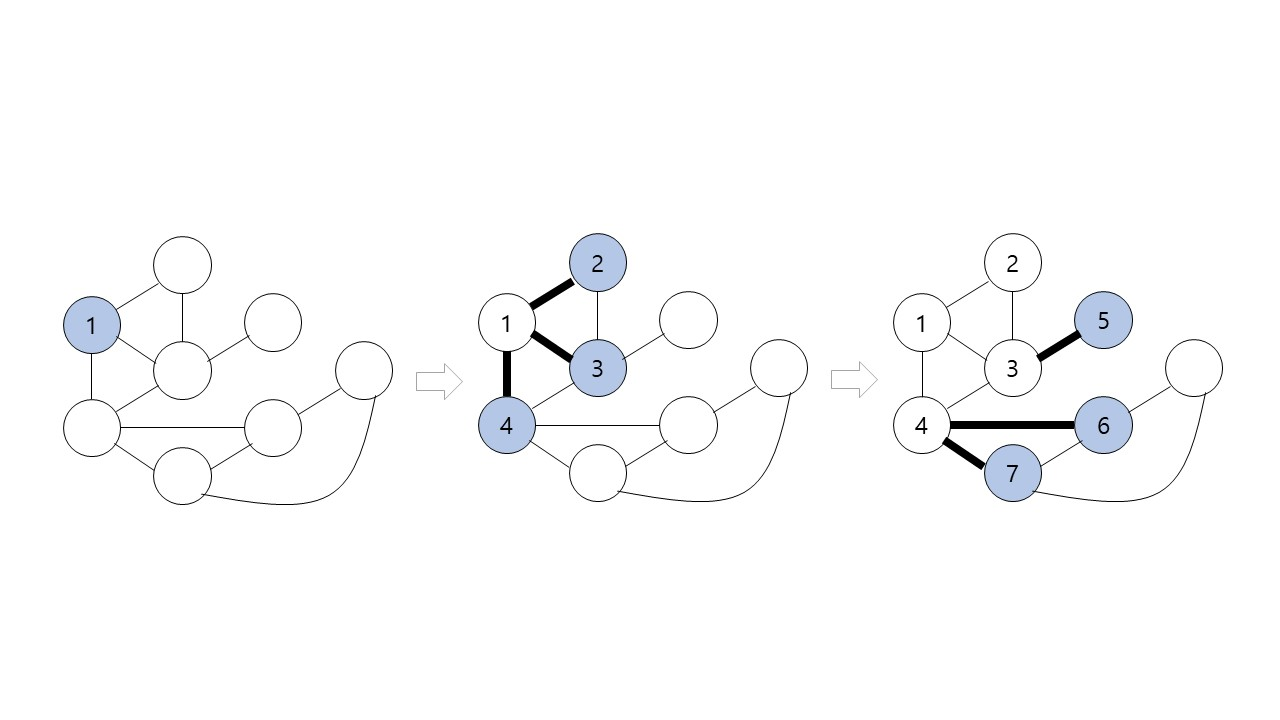
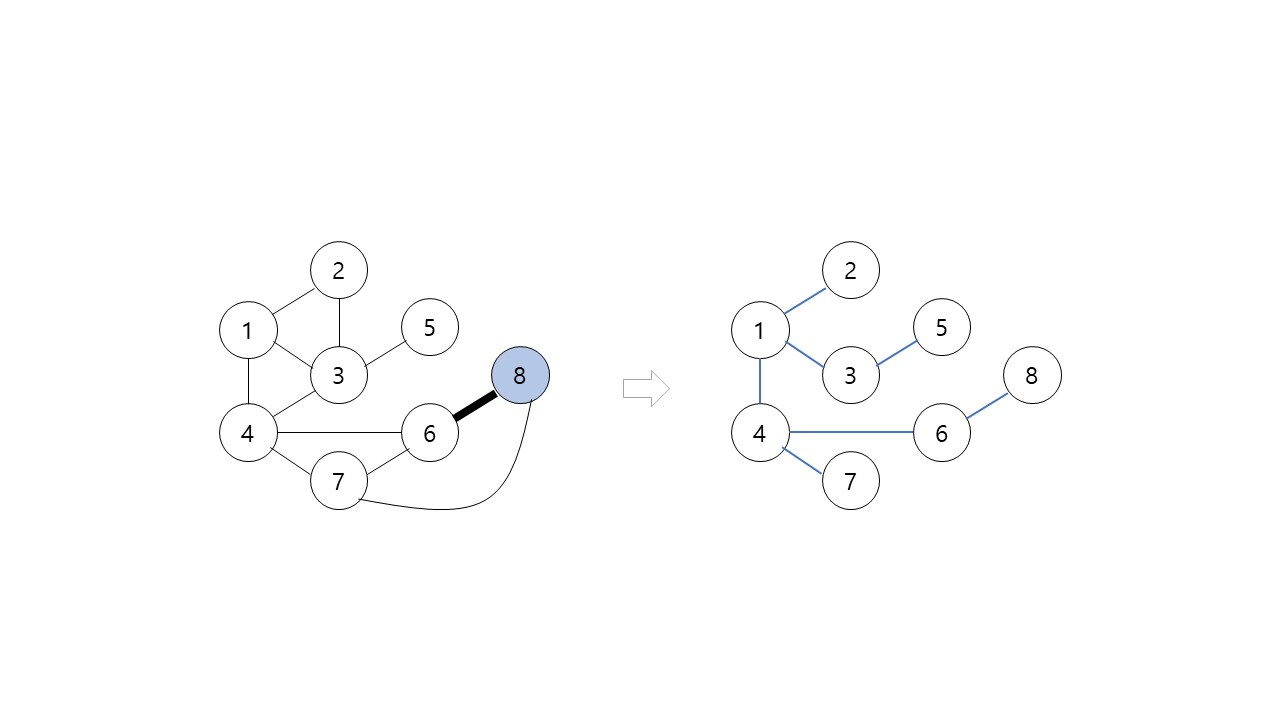
그림에서 검은색의 굵은 간선들을 각 정점을 처음으로 방문할 때 사용한 간선들이다. 그래프 G에서 이 간선들만 남기면 트리가 되는데 이 트리를 너비 우선 트리라 한다.
static void BFS(int S) {
Queue<Integer> q = new LinkedList<>();
q.add(S);
visited[S] = true;
while(!q.isEmpty()) {
int n = q.poll();
for(int i:list[n]) {
if(!visited[i]) {
visited[i] = true;
q.add(i);
}
}
}
}DFS(깊이우선탐색)
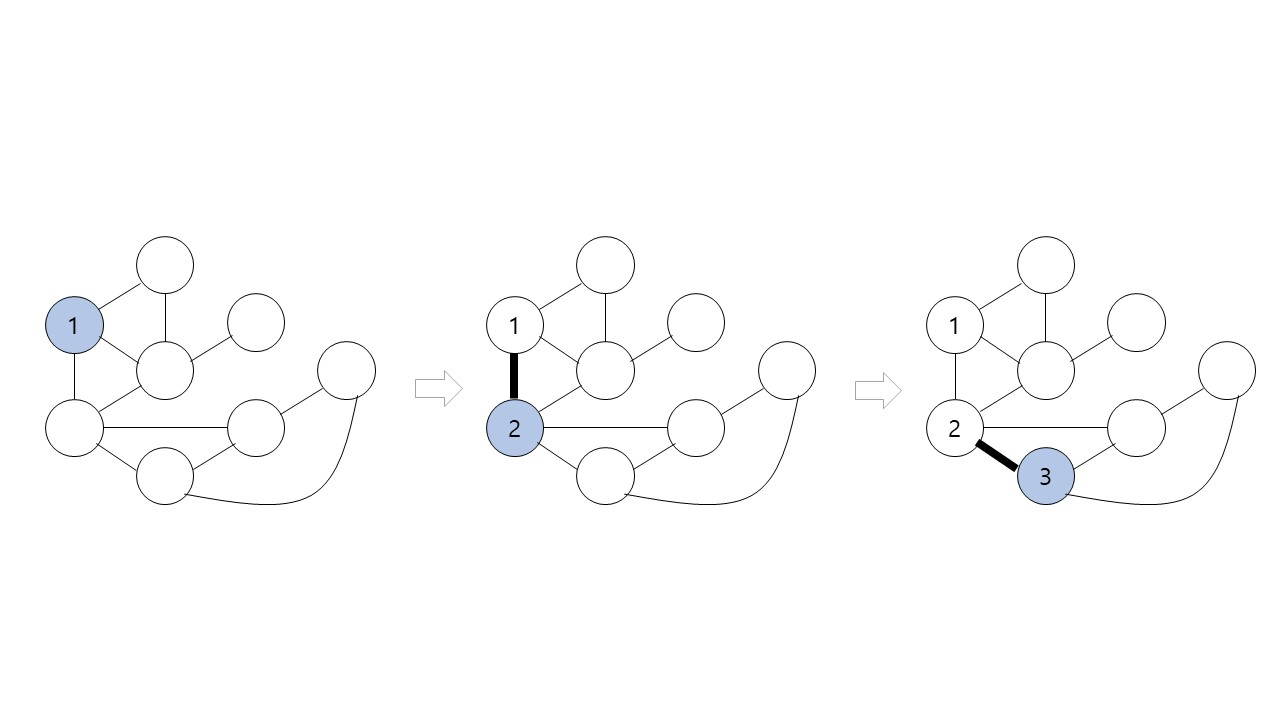
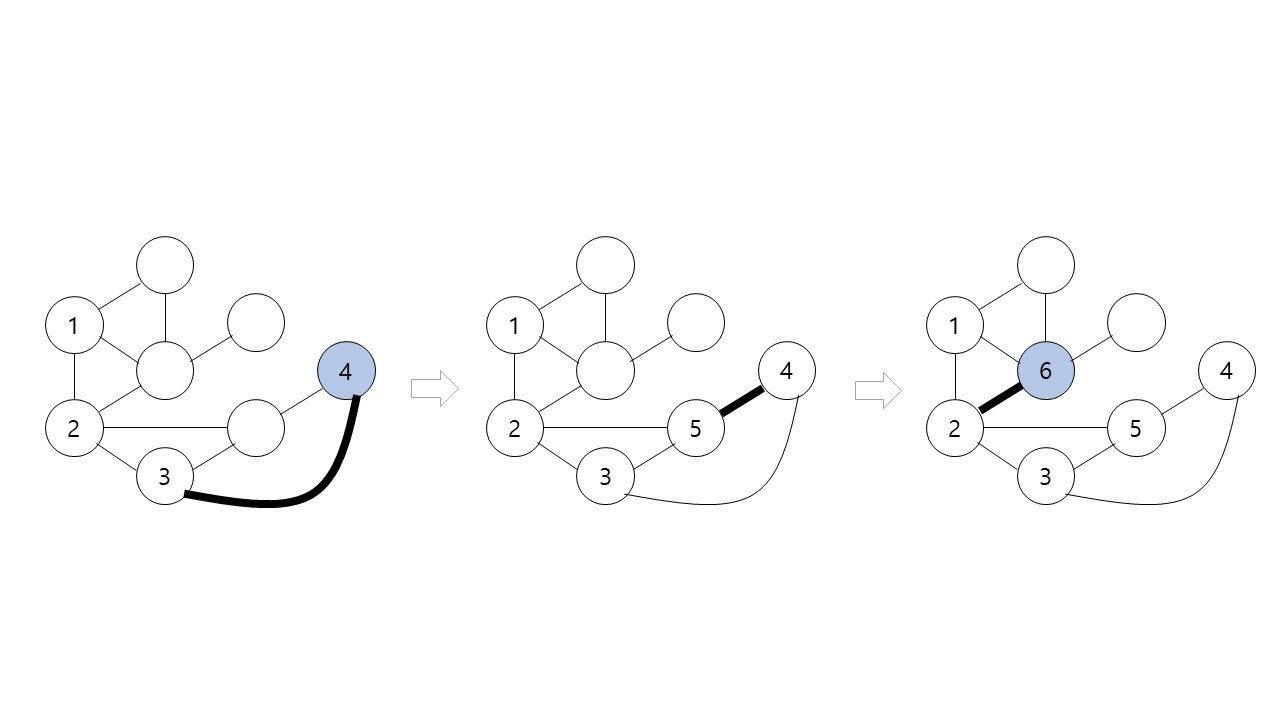
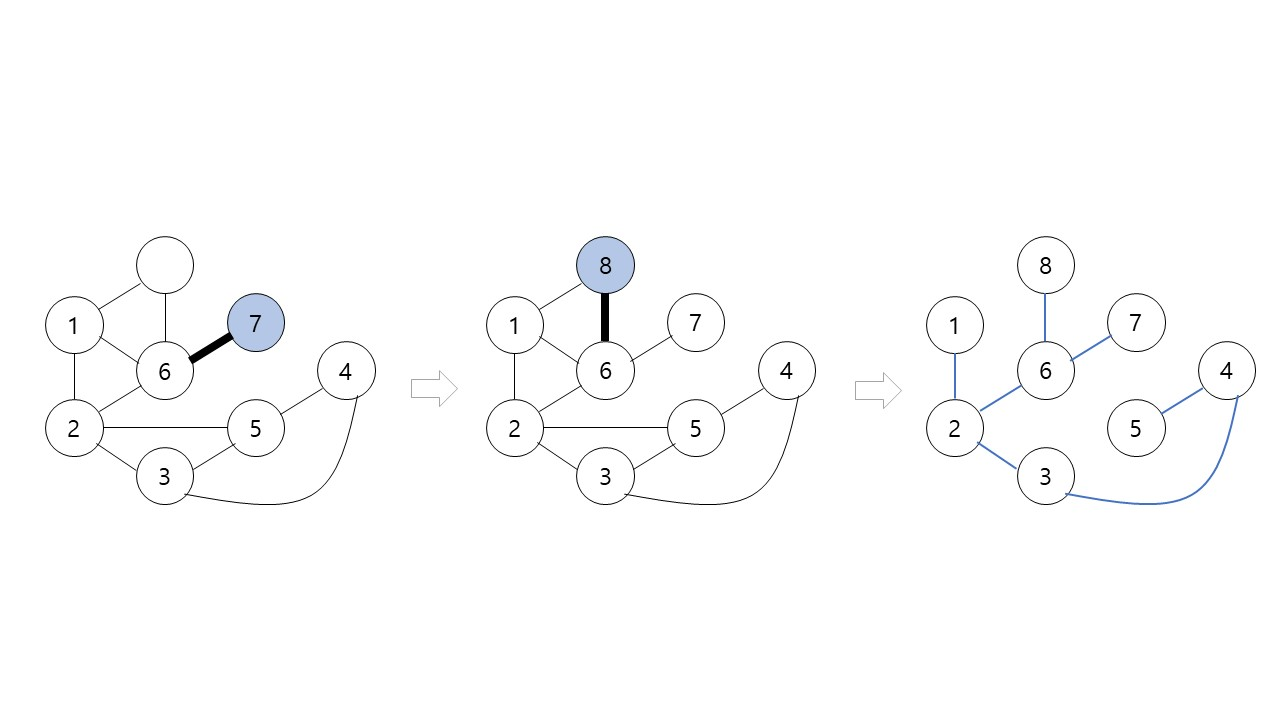
그림에서 검은색 굵은 간선들의 각 정점을 처음으로 방문할 때 사용된 간선들이다. 각 정점을 처음으로 방문할 때 사용한 간선들로 만들어진 트리이다.
두 그래프의 차이는 깊이먼저 탐색하냐 아니면 너비먼저 탐색하냐의 차이이다. 크게 스택과 큐의 성질을 따라 LIFO, FIFO로 진행된다. 너비우선탐색의경우 FIFO인 Queue를 사용하기때문에, 현재 노드에 연결된 정점들 먼저 방문하게된다. 이에 반대되게 깊이우선탐색은 LIFO인 Stack이나 재귀를 사용하기때문에, 현재 노드에 연결된 정점 중 1개를 끝까지 탐색하고 돌아온다.
static void DFS(int S) {
visited[S] = true;
for(int next : arr[S]){
if(!visited[next]){
dfs(next);
}
}
}