Abstract

고차원 시계열 예측은 수요 예측 및 금융 예측과 같은 많은 응용 분야에서 중요한 역할을 합니다. 현대의 데이터셋은 수백만 개의 상관된 시계열을 포함할 수 있으며, 이들은 매우 고차원적입니다 (개별 시계열당 하나의 차원을 가짐). 이러한 경우, 더 나은 예측을 위해 전역적인 패턴을 파악하고 지역적 보정을 활용하는 필요성이 있습니다. 그러나 최근 논문에서 소개된 대부분의 딥러닝 접근 방식은 일차원적입니다. 즉, 전체 데이터셋으로 훈련되지만 예측 중에 단일 차원의 미래 예측은 주로 해당 차원의 과거 값에 의존합니다. 이 논문에서는 이러한 결함을 보완하고 DeepGLO라는 딥러닝 기반 예측 모델을 제안합니다. 특히, DeepGLO는 전역 행렬 인수분해 모델과 시간 합성곱 네트워크로 규제된 혼합 모델로, 시계열의 지역적 특성과 관련된 공변량을 파악할 수 있는 또 다른 시간 네트워크를 결합합니다. 저희 모델은 다양한 고차원 시계열에서 효과적으로 훈련될 수 있으며, 서로 다른 시계열이 사전 정규화나 재척처리 없이도 크게 다른 스케일을 가질 수 있습니다. 실험 결과는 DeepGLO가 최첨단 접근 방식을 능가할 수 있다는 것을 보여줍니다. 예를 들어, 100,000차원 이상의 시계열을 포함하는 공개 데이터셋에서 다른 방법들에 비해 WAPE(Weighted Absolute Percentage Error)에서 25% 이상의 향상을 보여줍니다.

Introduction

시계열 예측은 소매 수요 예측, 금융 예측, 교통 또는 날씨 패턴 예측과 같은 다양한 산업 응용 분야에서 중요한 문제입니다. 일반적으로 비즈니스 프로세스 자동화에 중요한 역할을 합니다. 현대의 데이터셋은 수백만 개의 상관된 시계열과 수천 개의 시간 단위로 구성될 수 있습니다. 예를 들어, Amazon 또는 Walmart과 같은 온라인 쇼핑 포털에서는 한 카테고리 내의 모든 상품에 대한 미래의 일일 수요를 예측하는 것이 관심사일 수 있습니다. 이러한 경우, n개의 시계열을 예측해야하며, 과거의 수요 데이터를 기반으로 합니다. 이러한 시계열 데이터셋은 행렬 Y ∈ R n×t로 표현할 수 있으며, n은 수백만 단위의 크기일 수 있습니다.

전통적인 시계열 예측 방법은 개별 시계열 또는 소수의 시계열에 대해 작동합니다. 이러한 방법에는 잘 알려진 AR, ARIMA, 지수 평활, 고전적인 Box-Jenkins 방법론 및 일반적으로 선형 상태 공간 모델이 포함됩니다. 그러나 이러한 방법들은 수백만 개의 시계열이 포함된 대규모 데이터셋에서 개별 훈련이 필요하므로 확장성이 부족합니다. 또한 훈련 및 예측 중에 전체 데이터셋의 공유된 시간 패턴을 활용할 수 없습니다.

딥 네트워크는 비선형 시간 패턴을 모델링하는 능력으로 인해 최근 시계열 예측에서 인기를 얻고 있습니다. 순환 신경망(RNN)은 순차적 모델링에서 인기가 있으나 훈련 중 그래디언트 소멸/폭발 문제가 있습니다. 장기/단기 기억 네트워크(LSTM)는 이 문제를 완화시키고 언어 모델링 및 기타 seq-to-seq 작업에서 큰 성공을 거두었습니다. 최근에는 LSTM 블록을 내부 구성 요소로 사용한 딥 시계열 모델들이 등장했습니다. 또 다른 인기 있는 아키텍처는 LSTM과 경쟁력 있는 시간 합성곱/인과 합성곱을 사용한 wavenet 모델 로 시간 합성곱은 최근 시계열 예측에 사용되었습니다. 이러한 딥 네트워크 기반 모델은 전체 시계열 데이터셋에서 미니배치로 효과적으로 훈련될 수 있습니다. 그러나 이들은 여전히 두 가지 주요한 결함이 있습니다.

첫째, 위에서 언급한 대부분의 딥 모델은 개별 시계열의 스케일이 크게 다른 데이터셋에서 훈련하기 어렵습니다. 예를 들어 상품 수요 예측 사용 사례에서 인기 있는 상품의 수요가 특정 상품의 수요보다 수백 배 더 높을 수 있습니다. 이러한 데이터셋에서는 각 시계열이 적절하게 정규화되어야만 훈련이 성공하며, 그런 다음 예측 결과를 원래 스케일로 다시 변환해야합니다. 정규화의 모드와 매개 변수를 선택하는 것은 어렵고 다른 정확도를 초래할 수 있습니다. 예를 들어에서는 각 시계열을 해당하는 경험적 평균과 표준 편차를 사용하여 희백화합니다. 반면에서는 시계열이 첫 번째 시간 단계의 해당 값을 사용하여 스케일을 조정합니다.

둘째, 이러한 딥 모델들은 전체 데이터셋에서 훈련되었지만, 예측시 모델은 주로 지역적인 과거 데이터에만 초점을 맞춥니다. 즉, 예측을 위해 단일 시계열의 과거 데이터만 사용됩니다. 그러나 대부분의 데이터셋에서는 예측 시간에 전역적인 속성이 유용할 수 있습니다. 예를 들어 주식 시장 예측에서 Apple의 주식 가격을 예측하는 동안 Alphabet, Amazon의 주식 가격의 과거 값을 참고하는 것이 유익할 수 있습니다. 마찬가지로 소매 수요 예측에서 특정 상품의 미래를 예측하는 동안 비슷한 상품들의 과거 값도 활용될 수 있습니다. 이를 위해에서는 2D 합성곱과 순환 연결을 결합한 방법을 제안하여 입력 레이어에서 여러 시계열을 수용하여 예측 시간에 전역적인 속성을 포착합니다. 그러나 이 방법은 입력 레이어의 크기가 커지므로 몇 천 개의 시계열 이상에서는 확장할 수 없습니다. 또한 반대로, TRMF는 모든 시계열을 기저 시계열의 선형 조합으로 표현할 수 있는 시간적으로 규칙화된 행렬 인수분해 모델입니다. 이러한 기저 시계열은 예측 시에 전역적인 패턴을 포착할 수 있습니다. 그러나 TRMF는 선형 시간 종속성만 모델링할 수 있습니다. 또한 인수분해로 인한 근사 오차가 발생할 수 있으며, 이는 지역 초점의 부족으로 해석될 수 있습니다.

위의 논의를 바탕으로, 저희는 전역적인 사고와 지역적인 작용을 할 수 있는 딥러닝 모델을 제안하고자 합니다. 즉, 훈련과 예측 시에 지역 및 전역적인 패턴을 모두 활용하고, 스케일의 넓은 변동이 있는 경우에도 안정적으로 훈련될 수 있는 모델을 개발하고자 합니다.

Related Work

이 논문에서는 시계열 예측에 대한 최근 딥러닝 접근 방법에 초점을 맞추고 있습니다. 전통적인 방법에 대해서는 및 관련 참고 자료들을 읽어보시기를 권장합니다. 최근 몇 년 동안 딥러닝 모델들이 시계열 예측에서 인기를 얻고 있습니다.

DeepAR은 LSTM 기반 모델로, 미래 시간 단계의 베이지안 모델 파라미터를 LSTM의 해당 숨겨진 상태를 기반으로 예측합니다. 이 모델은 LSTM 블록을 사용하여 모든 시계열의 과거를 인코딩하고, 다중 지표 MLP 디코더를 사용하여 입력을 미래 예측으로 디코딩합니다. LSTNet은 2D 합성곱과 순환 구조의 조합을 통해 여러 시계열 사이의 상관 관계를 활용할 수 있습니다. 그러나 입력 레이어의 크기가 커지는 문제 때문에 이 모델을 몇 천 개의 시계열을 넘어서 확장하기 어렵습니다. 최근에는 시계열 예측에 Temporal convolutions이 사용되었습니다.

시간적 정규화를 갖춘 행렬 인수분해는 최초로 음성 제거 문제와 관련하여 사용되었습니다. TRMF 에서는 AR 기반의 시간적 정규화가 제안되었습니다. 본 논문에서는 이 작업을 확장하여 시간적 정규화를 시간적 컨볼루션 네트워크를 사용하여 비선형 설정에서 수행할 수 있습니다. 또한 글로벌 행렬 인수분해 모델과 시간적 컨볼루션 네트워크를 결합하여 로컬 및 글로벌 특성에 모두 초점을 맞출 수 있는 하이브리드 모델을 만듭니다.

Problem Setting

Proposed Method

LeveledInit: Handling Diverse Scales with TCN

Temporal Convolution Networks (TCN)에 대한 간단한 초기화 방법인 "LeveledInit"을 제안합니다. 이 방법은 다양한 스케일을 가진 고차원 시계열 데이터를 처리할 수 있도록 설계되었으며, 사전 정규화 없이도 안정적으로 학습할 수 있습니다. 앞서 언급한대로, 개별 시계열이 다양한 스케일을 가진 시계열 데이터셋에서는 깊은 신경망이 학습하기 어려울 수 있습니다. LSTM 기반 모델들은 이러한 데이터셋에서 안정적으로 학습되기 위해 사전 표준 정규화 또는 베이지안 평균 예측의 사전 스케일링이 필요할 수 있습니다. 정규화 파라미터의 선택은 예측 성능에 큰 영향을 미칠 수 있기 떄문에 아주 중요한 단계입니다.

Temporal Convolution:

먼저 TCN에 대해 간략히 설명드리겠습니다.
TCN은 다양한 레이어로 구성된 1D 컨볼루션 레이어와 dilation(확장)을 갖는 다층 신경망입니다. 레이어 i의 dilation은 일반적으로 dil(i) = 2^(i-1)로 설정됩니다.

필터 크기가 k이고 레이어 수가 d인 시간적 컨볼루션 네트워크는

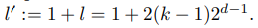
의 동적 범위를 갖습니다.
또한 모든 레이어에서 스트라이드가 1로 가정되며 레이어 i는 처음에 (k-1)dil(i)개의 제로 패딩이 필요합니다. 하나의 레이어당 하나의 채널을 갖는 시간적 컨볼루션 네트워크 예시를 그림 1a에 보여줍니다.
TCN은 이전 시계열 yJ 및 해당 시계열에 대한 과거 covariates zJ를 입력으로 받고, 한 스텝 앞으로 예측된 값 yˆJ +1을 출력하는 객체로 처리될 수 있습니다. TCN은 T(·|Θ)로 표기하며, 여기서 Θ는 매개변수 가중치입니다. 따라서 yˆ_J +1 = T(y_J, z_J|Θ)로 표기할 수 있습니다. 동일한 연산자들은 행렬에 대해서도 정의될 수 있습니다. Y ∈ R^(n×t), Z ∈ R^(n×r×(t+τ)), 그리고 행 인덱스 집합 I = {i1, ..., ibn} ⊂ [n]가 주어지면, Yˆ [I,J + 1] = T(Y[I,J ], Z[I, :,J ]|Θ)로 쓸 수 있습니다.

LeveledInit Scheme

한 가지 가능한 방법은 다양한 스케일로 인한 문제를 완화하기 위해 초기 네트워크 매개변수를 사용하여 지난 시간점 yj−l:j−1의 평균값을 대략적으로 예측하는 것으로 시작하고, 이를 미래 예측 yˆj로 사용하는 것입니다. 이후 훈련 과정에서 네트워크는 이 평균 주변의 변동을 예측하도록 학습할 것으로 기대됩니다. 이때, 이 평균 주변의 변동은 상대적으로 스케일이 자유로운 경우입니다. 이러한 초기화는 TCN의 일부 설정에 대해 간단한 초기화 기법인 "LeveledInit"이라고 합니다. 설명의 편의를 위해 과거의 covariates가 없고, 레이어 당 하나의 채널만 있는 경우를 고려해봅시다. 이 경우 초기화 기법은 각 레이어에서 필터 가중치를 1/k로 설정하는 것입니다. 이는 다음과 같은 명제를 얻게 됩니다.

???????????????? 각 커널 1/k로 두고 하는 것이 bias나 이런것은 업데이트 되겠지만 이게 왜 평균 주변의 변동을 학습하도록 ??? 그 bias를 평균주변의 변동이라고 보는건가????????

Proposition 1 (LeveledInit).

T (·|Θ)가 채널당 하나의 레이어, 필터 크기 k = 2 및 레이어 개수 d로 이루어진 TCN이라고 합시다. 여기서 Θ는 네트워크의 가중치와 편향을 나타냅니다. J = {j − l, ...., j − 1} 및 l = 2(k − 1)2d−1 일 때 [yˆj−l+1, · · · , yˆj ] := T (yJ |Θ)입니다. 만약 모든 편향이 0으로 설정되고 모든 가중치가 1/k로 설정된다면, y ≥ 0이고 모든 활성화 함수가 ReLU인 경우, yˆj = µ(yJ)입니다.

위의 명제는 LeveledInit이 필터 크기가 k = 2인 경우 (Fig. 1a 참조)에 TCN의 동적 범위 l을 고려하여 이전 l개의 시간점의 평균을 예측하는 결과를 도출한다는 것을 보여줍니다. 프로퍼지션 1의 증명은 내부 레이어의 활성화 값이 이전 레이어에서 들어오는 k개의 입력의 평균임을 보여주는 사실로부터 출발하며, 레이어에 대한 귀납법을 통해 결과를 얻습니다. LeveledInit는 상응하는 필터 가중치를 입력 레이어에서 0으로 설정하여 covariates 경우에도 확장할 수 있습니다. 또한 k = 2인 경우에는 쉽게 채널당 여러 층으로 확장할 수 있습니다. 6에서는 TCN이 LeveledInit으로 학습되어 사전 정규화 없이도 실제 데이터셋에서 신뢰성 있게 훈련될 수 있음을 보여줍니다. 또한 LeveledInit을 사용하여 TCN을 학습한 결과 Deep Leveled Network (DLN)라는 더 복잡한 변형에 대한 실험을 진행하였지만, LeveledInit의 간단한 초기화 방식이 DLN의 성능과 일치함을 관찰하였습니다.

DeepGLO: A Deep Global Local Forecaster

이 섹션에서는 전역 및 지역 특성을 모두 활용할 수 있는 하이브리드 모델인 DeepGLO를 소개합니다.

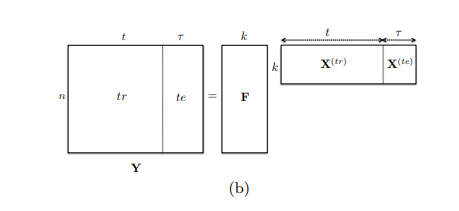
이 섹션에서는 시간 시리즈 예측을 위한 저랭크 행렬 인수분해 모델을 제안합니다. 이 모델은 정규화를 위해 TCN을 사용합니다. 아이디어는 학습 시간 시리즈 행렬 Y(tr)을 저랭크 요소 F ∈ R^n×k와 X(tr) ∈ R^k×t로 분해하는 것입니다. 여기서 k는 n보다 작습니다. 이것은 그림 1b에 설명되어 있습니다. 더 나아가, 우리는 X(tr) 행렬에서 시간 구조를 촉진하려고 합니다. 이로써 테스트 범위의 미래 값 X(te)도 예측될 수 있게 합니다. X = [X(tr)X(te)]라고 하면, X 행렬은 전체 데이터셋에서 전역적인 시간적 패턴을 포착하는 k개의 기저 시계열로 구성되며, 모든 원본 시계열은 이러한 기저 시계열의 선형 조합으로 볼 수 있습니다. 다음 소절에서는 TCN이 X의 시간 구조를 촉진하는 데 사용되는 방법에 대해 설명하겠습니다.

TCN을 사용하여 시간적 패턴을 포착하는 경우, 이 모델을 사용하여 X(tr)에 시간 구조를 촉진할 수 있습니다. 가정으로서 해당 네트워크를 TX(·)라고 합시다. 시간적 패턴은 다음과 같은 시간적 정규화를 목적 함수에 포함함으로써 촉진될 수 있습니다:

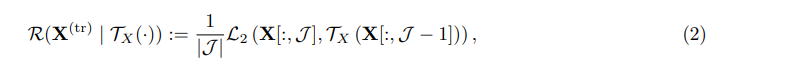
J = {2, · · · , t}이고 L2(·, ·)은 앞에서 정의한 제곱 손실 메트릭(metric)입니다. 이는 시간 스텝 {j − l, ..., j − 1} 사이의 과거 값에 대해 적용한 시간 네트워크의 예측과 시간 인덱스 j의 X(tr) 값이 가까운 것을 의미합니다. 여기서 l + 1은 섹션 4에서 정의한 네트워크의 다이나믹 레인지와 같습니다. 따라서 요약하면 요인과 시간 네트워크의 전체 손실 함수는 다음과 같습니다:

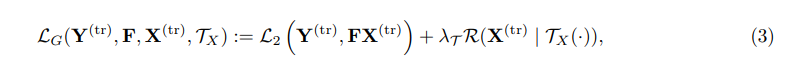
Train:

저차원 요인 F, X(tr) 및 시간 네트워크 TX(·)는 Eq. (3)의 손실을 근사적으로 최소화하도록 대체적으로 훈련될 수 있습니다. 전체 훈련은 미니배치 SGD를 통해 수행되며 두 가지 주요 구성 요소로 번갈아가며 수행됩니다: (i) 고정된 TX(·)의 경우, 요인 F, X(tr)에 대한 손실함수 LG(F, X(tr), TX)를 최소화하는 알고리즘 3을 사용합니다. (ii) 알고리즘 1을 사용하여 행렬 X(tr)에서 네트워크 TX(·)를 훈련합니다.

전체 알고리즘은 알고리즘 2에 상세히 설명되어 있습니다. TCN TX(·)는 먼저 LeveledInit으로 초기화됩니다. 그런 다음 두 번째 초기화 단계에서는 초기화된 TX(·)를 사용하여 두 요인 F와 X(tr)를 훈련합니다 (단계 3). 그 다음, itersinit 반복 동안 업데이트할 수 있는 itersalt 대체적인 단계가 이어집니다. F, X(tr) 및 TX(·)를 업데이트합니다 (단계 5-7).

Prediction

훈련된 지역 네트워크 TX(·)는 표준적인 방식으로 다중 단계 미래 예측에 사용될 수 있습니다. 기본 시계열의 과거 데이터 포인트 xj−l:j−1이 주어지면, 다음 시간 단계 xˆj의 예측은 [xˆj−l+1, · · · , xˆj ] := TX(xj−l:j−1)로 주어집니다. 이제 한 단계의 미래 예측은 과거 값과 연결하여 시퀀스 x˜j−l+1:j = [xj−l+1:j−1, xˆj]를 형성하고, 다음 예측을 얻기 위해 다시 네트워크를 통과시킬 수 있습니다: [· · · , xˆj+1] = TX(x˜j−l+1:j). 이와 같은 절차를 τ번 반복하여 미래로 τ개의 시간 단계를 예측할 수 있습니다. 따라서 우리는 테스트 범위 내의 기본 시계열을 얻을 수 있습니다 (Xˆ(te)). 최종 전역 예측은 Y(te) = FXˆ(te)로 주어집니다.

Combining the Global Model with Local Features

예측 작업은 훈련 원시 시계열 Y(tr)과 더불어 Z ∈ R
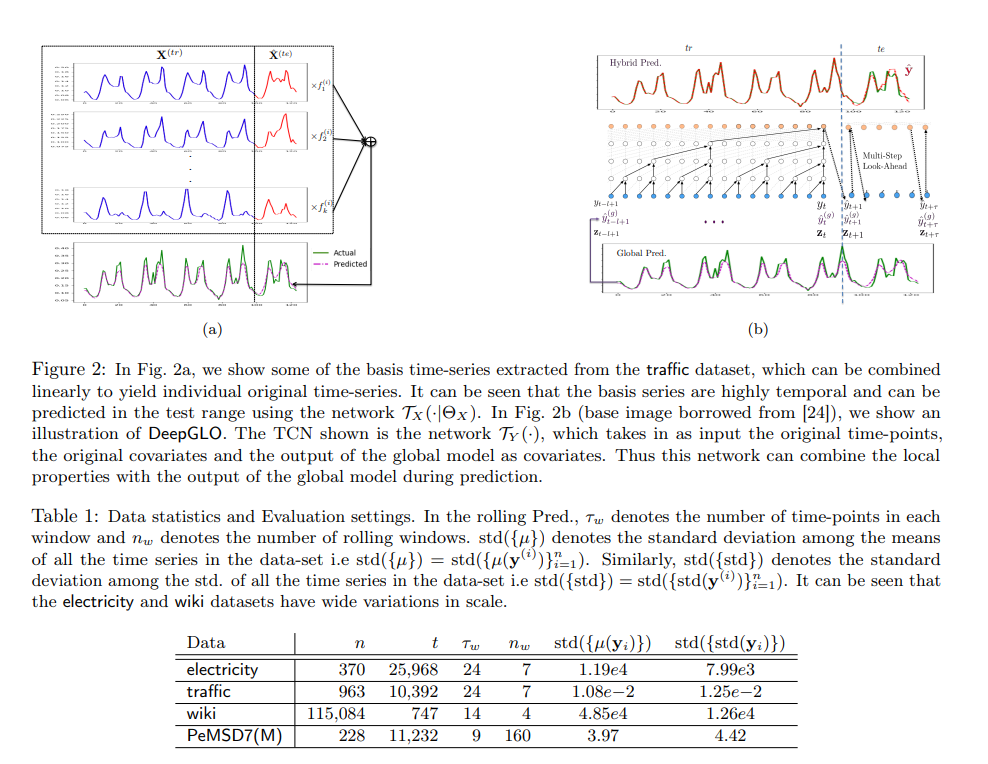
n×r×(t+τ)인 covariates를 입력으로 받습니다. 우리의 하이브리드 예측 모델은 입력 크기가 r+2인 TCN TY(·|ΘY)입니다: (i) 원시 원시 시계열의 과거 포인트를 위한 하나의 입력, (ii) 원래 r차원의 covariates를 위한 r개의 입력 및 (iii) 나머지 차원은 글로벌 TCN-MF 모델의 출력을 위해 예약되어 있으며, 이는 입력 covariates로 사용됩니다. 전체 모델은 그림 2에 설명되어 있습니다. 모델의 훈련 의사 코드는 알고리즘 4로 제공됩니다.

따라서 글로벌 TCN-MF 모델의 예측 결과를 TCN에 입력 covariates로 제공함으로써 최종 예측을 글로벌 데이터셋 전체 특성과 지역 시계열 및 covariates의 과거 값을 기반으로 합니다. DeepGLO는 롤링 예측과 다중 단계 미래 예측을 모두 수행할 수 있으며, 글로벌 TCN-MF 모델과 하이브리드 TCN TY(·)은 재학습 없이 예측을 수행할 수 있습니다. 그림 2의 데이터셋에서 추출한 몇 가지 기준 시계열(글로벌 특성) 예시를 그림 2a에 보여줍니다. 이러한 기준 시계열은 매우 시계열적이며 네트워크 TX(·|ΘX)를 사용하여 테스트 범위에서 예측할 수 있습니다. 그림 2b에서는 DeepGLO의 전체 아키텍처를 설명합니다. 글로벌 TCN-MF 모델의 출력이 TCN TY(·)에 입력으로 들어가고, 이를 지역적 특성과 결합하여 다중 단계 미래 예측을 통해 테스트 범위에서 예측합니다.