Abstract

제안하는 논문은 딥러닝에 규칙을 통합하는 새로운 훈련 방법인 "DEEPCTRL (Deep Neural Networks with Controllable Rule Representations)"입니다. DEEPCTRL은 모델에 규칙 인코더를 결합시키고 규칙 기반 목적 함수를 사용하여 의사 결정을 위한 공유 표현을 가능하게 합니다. DEEPCTRL은 데이터 유형과 모델 아키텍처에 대해 독립적이며, 입력과 출력에 대해 정의된 어떤 종류의 규칙에도 적용할 수 있습니다. DEEPCTRL의 핵심은 규칙 강도를 조정하기 위해 다시 훈련이 필요하지 않는다는 점입니다. 추론 단계에서 사용자는 정확성 대 규칙 확인 비율에 기반하여 원하는 작동 지점에 따라 조절할 수 있습니다. 물리학, 소매 및 의료와 같이 규칙을 통합하는 것이 중요한 현실 세계 도메인에서 DEEPCTRL의 효과를 보여줍니다. DEEPCTRL은 훈련된 모델의 신뢰성과 신뢰성을 크게 향상시켜 규칙 확인 비율을 크게 증가시키는 동시에 하류 작업에서 정확도 향상을 제공합니다. 또한 DEEPCTRL은 데이터 샘플에 대한 규칙의 가설 검정 및 데이터 세트 간의 공유 규칙을 기반으로 한 비지도적 적응과 같은 새로운 사용 사례를 가능하게 합니다.

Introduction

딥 신경망(DNN)은 이미지 분류, 기계 번역, 시계열 예측, 테이블 학습 등 여러 작업에서 뛰어난 성과를 거두고 있습니다. DNN은 훈련 데이터의 크기와 범위가 증가함에 따라 더 정확해집니다.
고품질과 대규모의 레이블이 지정된 데이터에 투자하는 것은 한 가지 방법이지만,
다른 한 가지 방법은 '규칙'이라고 불리는 사전 지식을 활용하는 것입니다
대부분의 시나리오에서 레이블이 지정된 데이터 세트는 작업에 대한 모든 규칙을 가르치기에 충분하지 않습니다. 물리학에서 예를 들어보겠습니다. 그림 1에 시각화된 이중 진자 시스템에서 다음 상태를 예측하는 작업을 고려했을 때,

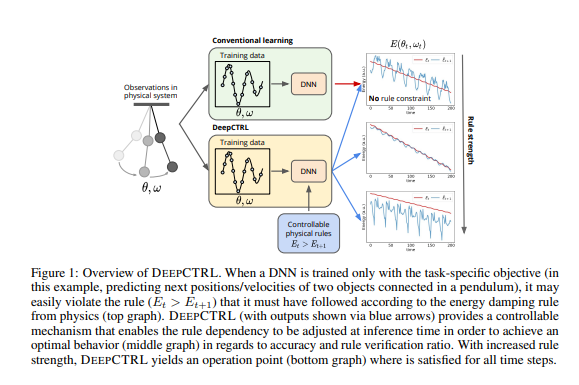
현재 상태에서 다음 상태로의 비교적 정확한 매핑을 기존의 지도 학습으로 피팅된 '데이터 기반' 블랙박스 모델이 할 수 있지만, '에너지 보존'이라는 규칙을 쉽게 포착하지 못할 수 있습니다.

해당 논문에서는 데이터 기반 작업을 위해 데이터로부터의 학습 외에도 DNN이 규칙에서 지식을 흡수하는 효과적인 방법에 초점을 맞추고 있습니다. 규칙으로부터 학습하는 것의 이점은 다양합니다.
첫째, 규칙은 데이터 감독이 최소한인 경우 추가 정보를 제공하여 테스트 정확도를 향상시킬 수 있습니다.

둘째, 규칙은 DNN의 신뢰성과 신뢰성을 향상시킵니다.
DNN의 널리 사용되지 못하는 주요 이유는 '블랙박스'로써의 한계입니다. 추론 이유에 대한 이해 부족과 사람의 판단과의 불일치로 인해 사용자의 신뢰도가 감소하기 때문.
규칙을 통합함으로써 이러한 불일치를 최소화하고 사용자의 신뢰도를 향상시킬 수 있습니다. 예를 들어, 대출 연체 예측을 위한 DNN이 은행에서 사용하는 모든 결정 휴리스틱을 흡수할 수 있다면, 은행의 대출 담당자들은 예측에 더욱 편안하게 의존할 수 있습니다.

셋째, DNN은 인간이 인지하기 힘든 입력의 작은 변경에 민감합니다. 규칙을 사용하면 모델의 검색 공간이 축소되어 불명확성을 감소시키기 위해 이러한 변경의 영향을 최소화할 수 있습니다. '데이터 기반' 및 '규칙 기반' 학습을 함께 고려할 때 기본적인 질문은 각각의 기여도를 어떻게 균형 있게 조절할 것인가입니다. 예를 들어, 어떤 규칙이 계속 유지된다고 할 때(자연과학 처럼), 규칙 기반 학습의 기여도를 임의로 증가시키는 것은 바람직하지 않습니다.(파라미터) 데이터셋뿐만 아니라 각 샘플에도 의존하는 최적의 트레이드오프가 있기 떄문. 따라서 데이터 및 규칙 기반 학습의 기여도(파라미터)를 제어할 수 있는 프레임워크는 가치가 있습니다. 이러한 제어는 계산 비용을 최소화하고 배포 시간을 단축하며 다양한 샘플이나 변화하는 분포에 유연하게 조정하기 위해 추론 단계에서 가능해야 합니다.

본 논문에서는 레이블이 지정된 데이터와 규칙으로부터의 공동 학습을 가능하게 하는 DEEPCTRL을 제안합니다. DEEPCTRL은 데이터와 규칙에 대해 각각 별도의 인코더를 사용하며, 중간 표현을 커버하기 위해 결과를 확률적으로 결합합니다. 다시 훈련하지 않고 추론 단계에서 규칙 강도를 점진적으로 증가/감소시킬 수 있게 해줍니다. 또한, 비분리 가능한 규칙을 차별화 가능한 목적으로 변환하기 위해 새로운 퍼터베이션 기반 방법을 제안합니다. DEEPCTRL은 데이터 유형이나 모델 아키텍처에 대해 독립적이며, 다양한 작업과 규칙에서 유연하게 사용할 수 있습니다.
(i) 추론 시에 규칙 강도만 조정하여 규칙 확인 비율을 크게 향상시키고 정확도를 향상시킵니다;
(ii) 훈련 없이 최적의 규칙 강도 비율에 따라 각 샘플에 대한 가설을 조사할 수 있는 기능을 제공합니다
(iii) 규칙의 강도를 변경함으로써 대상 작업의 성능을 향상시킵니다. 이는 데이터의 서로 다른 하위 집합이 서로 다른 강도의 규칙을 충족시키는 것을 알고있을 때 원하는 능력

Related Work

다양한 방법들이 연구되어 왔으며, 규칙을 딥러닝에 통합하여 다양한 응용 분야에서 사전 지식을 고려하는 것이 가능해졌습니다. 예측에 규칙을 주입하는 접근 방식 중 하나로는 후방 정규화(Posterior regularization)이 있습니다.
또한 Teature-Student 프레임워크를 사용하여, Teature 네트워크를 Student 네트워크dp (논리적인) 규칙 정규화 하위 공간으로 사영하고, 학생 네트워크는 교사의 출력을 흉내 내는 것과 레이블을 예측하는 것 사이의 균형을 맞추기 위해 업데이트됩니다.

DEEPCTRL은 이와는 다르게 규칙을 주입하는 방식에서 차별화되며, 훈련 없이 추론 시에 규칙 강도를 조절할 수 있는 측면에서 독특합니다. 이는 데이터 매니폴드에서 규칙 표현의 정확한 학습에 의해 가능해지며, 단순히 목표 정확도에 대한 규칙 확인을 개선하는 것 이상의 새로운 능력을 제공합니다.

Proposed Method

Learning Jointly from Rules and Task

아래 목적식은 규칙(rule) 위반을 나타내는 항목과 지도 학습 작업의 학습 목적을 결합하는 것을 통해 규칙을 통합하는 Loss Function입니다.

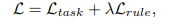
여기서 λ는 규칙 기반 목적의 계수입니다. 우리는 이 접근 방식의 세 가지 제한 사항을 해결하고자 합니다:
(i) λ는 학습 전에 정의되어야 합니다(예: 검증 점수로 안내되는 하이퍼파라미터일 수 있음),
(ii) 추론 시 대상 데이터와 학습 설정 간에 불일치가 있는 경우 λ를 대응하여 조정할 수 없습니다, 그리고
(iii) Lrule은 학습 가능한 매개변수에 대해 미분 가능해야 합니다.

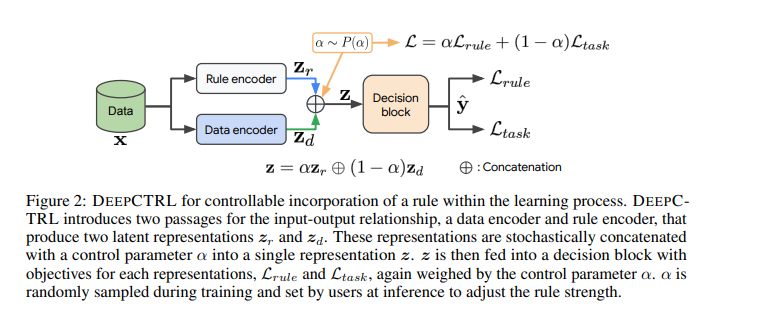
DEEPCTRL은 규칙 표현(rule representation)을 만들고, 데이터 표현(data representation)과 결합하여, 규칙의 강도를 추론 시간(inference time)에 제어할 수 있도록 하는 것이 핵심입니다. Fig. 2에서는 DEEPCTRL의 개요를 보여주고, Algorithm 1은 해당 학습 프로세스를 설명합니다. 우리는 데이터 인코더 φd와 규칙 인코더 φr을 도입하여 입력-출력 관계를 두 개의 단계로 수정합니다. 이렇게 함으로써 각 인코더는 레이블된 데이터와 규칙으로부터 추출된 정보에 대한 잠재적 표현(zd와 zr)을 개별적으로 학습하도록 합니다. 그런 다음, 두 개의 표현은 확률적으로 연결(연산 기호로 ⊕로 표시)되어 단일 표현 z를 얻습니다. 데이터 인코딩 대비 규칙 인코딩의 상대적 기여를 조절하기 위해, 랜덤 변수 α ∈ [0, 1]를 사용하며,

α는 P(α)에서 샘플링됩니다. 랜덤한 α를 사용하는 동기는 다양한 값의 매핑을 학습하는 것을 촉진하여 추론 시에 모델이 특정한 선택된 값을 가지고 높은 성능을 발휘할 수 있도록 하는데 있습니다.

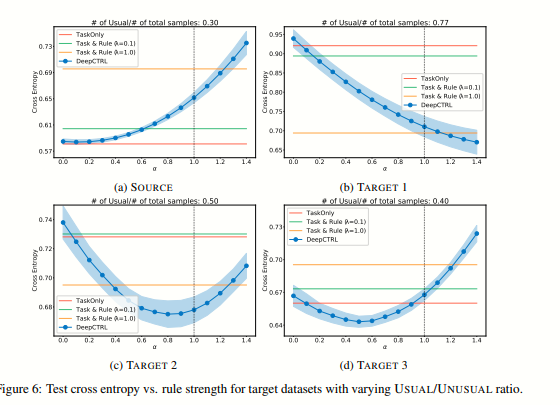
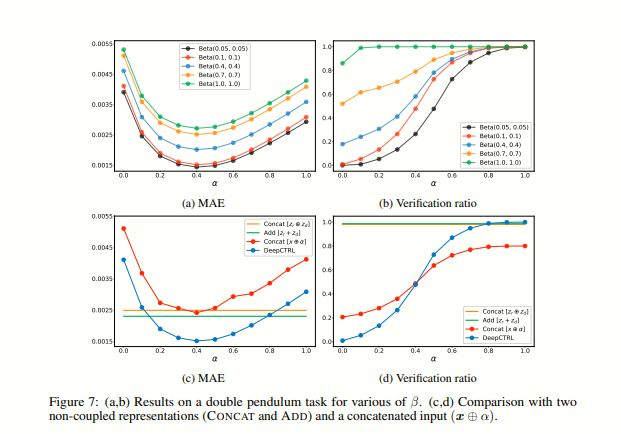
DEEPCTRL에서 추론 시에 제어 매개변수인 α를 수정함으로써 사용자는 모델의 동작을 조정하여 새로운 데이터에 적응시킬 수 있습니다. 규칙의 출력 결정에 대한 강도는 α의 값을 증가시킴으로써 강화될 수 있습니다. α를 0으로 설정하면 추론에서 규칙의 기여가 최소화되지만, 실험에서 보여진 것처럼, 훈련 과정에서 다양한 α 값이 고려되기 때문에 결과는 여전히 기존 훈련보다 우수할 수 있습니다. 일반적으로 중간값의 α 값은 특정 성능, 투명성 및 신뢰성 목표에 따라 최적의 솔루션을 얻을 수 있습니다. 또한, α가 0이거나 1에 가까워질 때 모델이 명확하고 강건한 동작을 보여주며 이후의 보간에 정확하게 적용될 수 있도록 보장하기 위해, 우리는 [0, 1]에서 균일하게 샘플링하는 대신에 α를 더 강조적으로 극단 부근에서 샘플링하는 것을 제안합니다. 이를 위해 Beta 분포 (Beta(β, β))에서 샘플링하는 방식을 선택합니다.

Ltask와 Lrule의 스케일 차이는 DEEPCTRL의 모든 학습 가능한 매개변수가 α와 관계없이 특정 목적에 지배되어 균형이 깨질 수 있다는 우려가 있습니다. 이는 DEEPCTRL의 표현 능력을 제한하고 수렴을 단일 모드로 유도하는 원하지 않는 동작입니다. 예를 들어, Lrule이 Ltask보다 훨씬 큰 경우, α가 0에 가까워져도 DEEPCTRL은 규칙 기반 모델이 됩니다. 이러한 균형이 깨진 동작을 최소화하기 위해 스케일 조정을 자동으로 수행합니다. 학습 프로세스를 시작하기 전에, 훈련 세트에서 초기 손실 값인 Lrule,0와 Ltask,0를 계산하고 스케일 매개변수인 ρ = Lrule,0/Ltask,0를 도입합니다. 따라서 DEEPCTRL의 목적 함수는 다음과 같이 변화합니다.

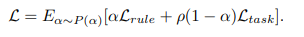
Integrating Rules via Input Perturbations

모델을 학습하기 위해 L_rule을 미분가능한 함수로 만들어줘야합니다.
예를 들어 rule이 r(x, yˆ) ≤ τ로 정의 되었고 r이 미분가능한 함수 일때 L_Rule = max(r(x, yˆ)-τ,0) 으로 정의될 수 있습니다. (해당 뜻은 violation 즉, 사용자가 정의해 놓은 rule을 벗어났을 때, 벗어난 만큼 페널티를 주겠다는 뜻입니다.)
그러나 입력 x 또는 학습 가능한 매개변수에 대해 미분 불가능한 규칙들이 많이 존재하며, 이러한 경우 위에서 정의한 연속 함수 Lrule을 정의하는 것이 불가능할 수 있습니다.
예를 들어, 'j번째 클래스 yˆj의 확률이 a < xk (여기서 a는 상수이고 xk는 k번째 특징입니다) 일 때 높아진다'와 같은 규칙

이러한 문제점을 보완하기 위해 perturbation method를 제안했습니다.

알고리즘 2에 개요된 입력 변조 방법을 도입하여 미분 가능하지 않은 제약 조건에 DEEPCTRL을 일반화합니다. 이 방법은 입력 특징 x에 작은 변조량 δx (알고리즘 2의 4번째 줄)를 도입하여 원래의 출력 yˆ을 수정하고 그에 대한 규칙 기반 제약 조건 Lrule을 구성하는 것입니다. 예를 들어, 이전 단락에서 언급한 첫 번째 샘플 규칙 (부울 규칙의 연결)을 통합하려면, xk < a이고 a < xp,k인 경우만 xp를 유효한 변조된 입력으로 고려하며, yˆp는 xp에서 계산됩니다. Lrule은 다음과 같이 정의됩니다:

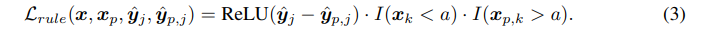
Experiment

EEPCTRL을 물리학, 소매 및 의료 분야의 기계 학습 사례에 대해 평가하였습니다. 이러한 분야에서 규칙의 활용은 특히 중요합니다.

규칙 인코더 (φr), 데이터 인코더 (φd) 및 결정 블록 (φ)에는 중간 레이어에서 ReLU 활성화 함수를 사용하는 MLP를 사용하였으며, 우선 DEEPCTRL을 α = 0으로 고정된 TASKONLY 기준과 비교하였습니다. 즉, 데이터 인코더 (φd)와 결정 블록 (φ)만 사용하여 다음 상태를 예측합니다. 또한, TASKONLY에 규칙 정규화를 적용한 TASK&RULE도 포함시켰습니다. 이는 Eq. 1을 사용하고 λ를 고정한 방식입니다. 또한, 규칙을 강제하는 Lagrangian Dual Framework (LDF)와 비교하였습니다. LDF는 제약 최적화 문제를 푸는 방식으로 규칙을 강제합니다.

Improved Reliability Given Known Principles

DEEPCTRL은 제어 매개변수 α를 조정함으로써 더 높은 규칙 검증 비율과 따라서 더 신뢰할 수 있는 예측을 달성할 수 있습니다. 더 좋은 검증 비율에서 작동하는 것은 성능에 유리할 수 있습니다.

Results on accuracy and rule teaching efficacy

Fig. 3은 제어 매개변수가 작업 기반 측정 및 규칙 기반 측정에 어떤 영향을 미치는지를 보여줍니다. DEEPCTRL에서 추가로 통합된 규칙은 다음 상태 xˆt+1의 예측을 더 정확하게하는 데 매우 유용합니다.
TASKONLY와 비교하면 DEEPCTRL은 예측 MAE를 크게 줄입니다. 매개변수는 도메인 지식 제약 조건과 함께 더 나은 표현을 학습하기 위해 조정됩니다. 또한, DEEPCTRL은 TASKONLY보다 훨씬 높은 검증 비율을 제공하며 더 안정적입니다 (TASK&RULE에 근접) (Fig. 3c). 이는 DEEPCTRL이 데이터 주도 모델에 도메인 지식을 통합하여 신뢰할 수 있고 견고한 예측을 제공할 수 있다는 것을 보여줍니다. DEEPCTRL은 재훈련 없이 α를 조정하여 모델의 동작을 제어할 수 있습니다.

Comparison to baselines

Fig. 3(a, b)은 DEEPCTRL을 고정된 정규화 항으로 규칙 기반 제약 조건과 비교한 것을 보여줍니다. 우리는 다른 λ ∈ {0.01, 0.1, 1.0}을 테스트하였고, 모두 추가적인 정규화 (Eq. 1)가 두 측면에 도움이 되었습니다. 가장 높은 λ는 가장 높은 검증 비율을 제공하지만, 예측 오류는 λ = 0.1보다 약간 더 나쁩니다. DEEPCTRL과 비교하여 고정된 기준의 가장 낮은 예측 오류는 DEEPCTRL의 것과 비교 가능하거나 (심지어 더 큰 경우도 있음) 그보다 큽니다.

그러나 고정된 기준의 가장 높은 검증 비율은 여전히 DEEPCTRL의 것보다 낮습니다. 또한,LDF로 규칙 제약을 부과하는 벤치마크를 고려하고, 그 결과를 검증 세트에서 가장 낮은 MAE (LDF-MAE)와 가장 높은 검증 비율 (LDF-RATIO)에 따라 선택한 두 가지 결과를 보여줍니다.
LDF는 DEEPCTRL처럼 추론 시에 유연하게 규칙 강도를 변경하는 기능을 허용하지 않기 때문에 이러한 운용점을 찾기 위해 다양한 하이퍼파라미터로 재훈련해야 합니다. LDF-MAE는 테스트 세트에서 다른 모든 결과보다 높은 MAE와 낮은 검증 비율을 제공하여 학습된 규칙 동작의 일반성이 부족함을 보여줍니다. 반면, LDF-RATIO는 다른 모든 결과보다 낮은 MAE를 제공합니다. 그러나 검증 세트의 검증 비율이 50%만 따르기 때문에 메소드의 신뢰성이 크게 낮아집니다. 이러한 결과들은 DEEPCTRL이 고정된 방법들인 LDF와 비교하여 MAE에서 경쟁력을 보여주며, 규칙 검증 비율을 더 유리한 포인트에서 조정할 수 있는 유연성을 제공하고, 추가 기능들을 가능하게 한다는 것을 보여줍니다.

Scale of the objectives

Lrule과 Ltask의 스케일이 균형을 이루도록 조정하는 것은 모든 학습 가능한 파라미터가 하나의 목적에 지배되지 않도록 하는 데 중요합니다. 제안된 스케일 파라미터 ρ를 사용하여 α → 0과 α → 1에 대해 두 가지 극단에서 L의 스케일이 비슷하도록 해야 합니다. Fig. 3a는 이러한 스케일 조정이 더 U자형 곡선을 가능하게 하며, α → 0일 때의 검증 비율이 Fig. 3b에서의 TASKONLY와 근접함을 보여줍니다. 다시 말해, DEEPCTRL은 α → 0일 때 TASKONLY와 가깝고, α → 1.0일 때는 RULEONLY에 가깝다는 것을 의미합니다. 훈련을 시작하기 전에 초기 손실 값 Lrule,0과 Ltask,0를 사용하여 스케일 파라미터를 고정하므로, 스케일 파라미터를 검색할 필요가 없습니다.

Optimizing rule strength on validation set

DEEPCTRL을 재훈련하지 않고도 원하는 α 값을 사용하여 추론할 수 있습니다. Fig. 3에서는 검증 세트에서 목표 검증 비율에 기반하여 최적의 α를 선택하는 시나리오를 고려합니다. 검증 세트에서 90% 이상의 검증 비율을 위해 α > 0.6이 필요하며, 이는 테스트 세트에서 80.2%의 검증 비율을 보장합니다. 반면, 고정된 목적 함수 ('Task & Rule') 벤치마크의 λ를 90% 이상의 검증 검증 비율에 대해 최적화하는 경우, 테스트 검증 비율이 71.6%로 DEEPCTRL보다 8.6% 낮습니다. 또한, 검증 세트의 검증 비율을 사용하여 오류를 최소화하는 규칙 강도를 결정할 수 있습니다. 검증 세트에서 최소 MAE는 α = 0.2일 때 발생하며, 이는 규칙 검증 비율이 약 60%인 것과 대응합니다. 테스트 세트에서도 동일한 규칙 검증 비율 60%를 만족하는 α를 찾으면, α = 0.4가 최적으로, 또한 가장 낮은 MAE를 제공합니다. 다시 말하면, 규칙 검증 비율은 DEEPCTRL의 로버스트한 비지도 모델 선택 프록시이며, 학습된 표현의 일반성을 강조합니다.