필요성

비대칭 암호화를 이용해 데이터에 대한 기밀성을 보장이 가능하다.(ex : AES, ARIA 등) 그러나 비대칭 암호화를 사용할 경우 미리 서로 비밀키를 공유하는 과정에서 발생하는 문제를 방어하기가 어렵다. 이런 어려움 때문에 공개키 기반의 암호가 연구 되었다.

대표적인 공개키 암호 RSA

대표적인 공개키 암호인 RSA는 연구자의 이름을 따서 RSA로 이름을 지었고, 쉽게 접할수 있는 부분이 SSH키 생성기에서 default로 생성을 할경우 RSA-4096으로 생성이 된다. 여기서 4096 bit의 키값을 생성한다는 의미다.

RSA 원리

Ke : 공개키(Public Key)
Kd : 개인키(Private Key)
N : 임의의 두 소수 p, q의 곱
m : 메시지
일단 f()를 특정 함수라고 가정한다. f(Ke, N) 으로 부터 f(Kd, N)을 도출하기가 어려울 경우 f(Ke,N)을 공개적으로 알려줘도 보안상 문제 없이 배포가 가능하다.

암호화 알고리즘은
E(Ke, N, m) = m^Ke Mod N , KeKd mod (p-1)(q-1) == 1 을 동시에 만족함
복호화 알고리즘은
D(Kd, N, c) = c^Kd Mod N

위 알고리즘을 적용하여 RSA를 이용하여 키를 공유하는 방법은
1. p, q를 미리 설정
2. Ke 를 설정 (공개키 설정)
3. KeKd mod (p-1)(q-1) == 1 이 되는 Kd 설정
키를 공유할 수 있게됨.

디피 헬만 키교환

공개키 암호는 아니고, 키 교환을 위한 알고리즘으로 사용됨
이산 로그 문제를 사용하여 키 교환을 수행함
이산 로그 문제란 y = M ^ x mod p 에서 M, x, p를 알경우 y를 구하긴 쉬우나, y, M, p를 알경우 x를 구하기 어렵다는 것이다.

알고리즘

이 문제를 사용하여 공개키를 교환하는 알고리즘이 디피 헬만 알고리즘으로
A, B 두 서버가 서버의 비밀키 a, b를 생성했다고 치자
특정 값 g에 대해서 아래와 같이 연산하여 공개키를 생성한다.
Ae = g ^ a mod p
Be = g ^ b mod p
A : Be ^ a = g ^ (ab) mod p = Ad
B : Ae ^ b = g ^ (ab) mod p = Bd
처럼 계산하여 두 서버는 Ad == Bd 같은 비밀키를 공유하게 된다.

취약점

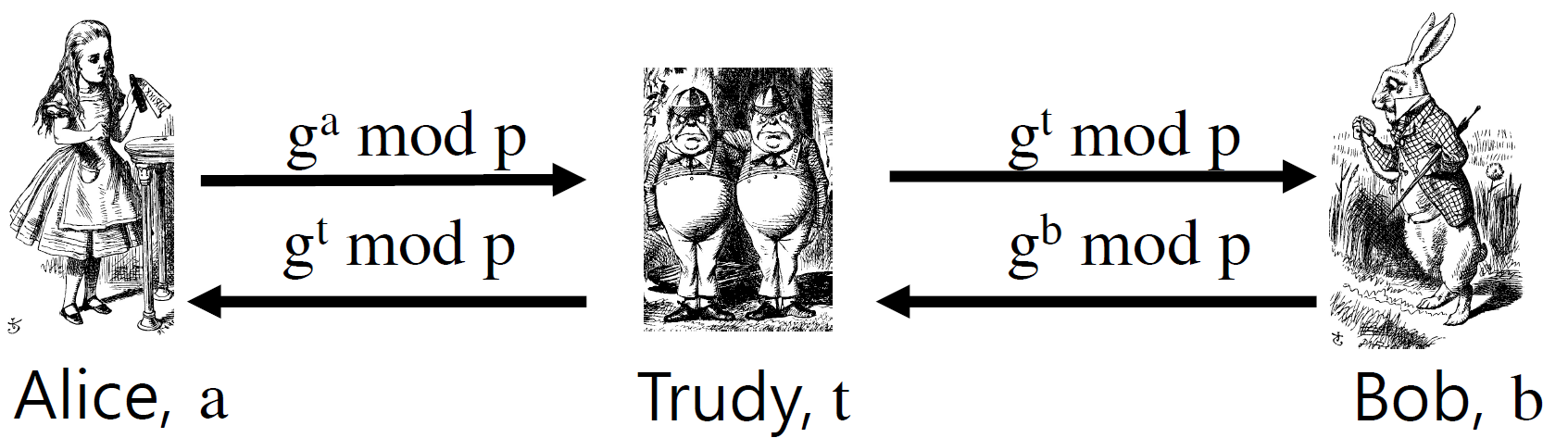
MIM(Man In the Middle) 공격에 취약하다.
즉 서로 주고 받는 각자의 공유키 값을 탈튀하고 g^t, g^t 값으로 변경시켜 공유 시킬 경우
A : g ^ t ^ a mod p = Ad
B : g ^ t ^ b mod p = Bd
개인키를 사용하게 됨 공격자는 Ad, Bd값을 모두 알게됨