Ch 07. NP-완전 문제 (1)

7.1 컴퓨터로 풀 수 있는 문제 분류

1) P 문제 집합

• 다항식 시간복잡도 가진 알고리즘으로 해결되는 문제들
  • $O(log n), O(n), O(nlogn),...$

2) NP 문제 집합

• NP 문제
  • 다항식보다 큰 시간복잡도를 가진 알고리즘으로 해결되는 문제들
• NP 알고리즘
  • 비결정적 다항식 시간 알고리즘
  • 해를 찾는 알고리즘 아님!
  • 해를 다항식 시간 안에 확인하는 알고리즘(yes or no)
  • 상수를 사용한 결정 문제로의 변형 필요

    여행자 문제

    각 도시를 한 번씩만 방문하고 시작 도시로 돌아오는 최단 경로의 거리를 찾는 문제
    8개 도시 (A B C D E F G H)

    • 상수 K를 사용하여 결정 문제로 변형
      각 도시를 1번씩만 방문하고 시작 도시로 돌아오는 경로의 거리가 K보다 짧은 경로가 있는가?
      
      
    • 하나의 해를 추측
      A G D H F E B C를 추측했다고 가정
      
      
    • 추측한 해의 값을 계산 => 선형 시간에 계산됨
      해의 값 = (A와 G 사이의 거리)
      + (G와 D 사이의 거리)
      + (D와 H 사이의 거리)
      ……
      + (B와 C 사이의 거리)
      + (C와 A 사이의 거리)
      
      
    • 해의 값이 K보다 작으면 ‘yes’라고 답

2)-1. NP-완전 문제 집합

• 지수 시간 시간복잡도를 가진 알고리즘으로 해결되는 문제들
• 어느 하나의 NP-완전 문제에 대해서 다항식 시간의 알고리즘을 찾아내면 모든 다른 NP-완전 문제도 다항식 시간에 해를 구할 수 있다.
  

7.2 NP-완전 문제 특성

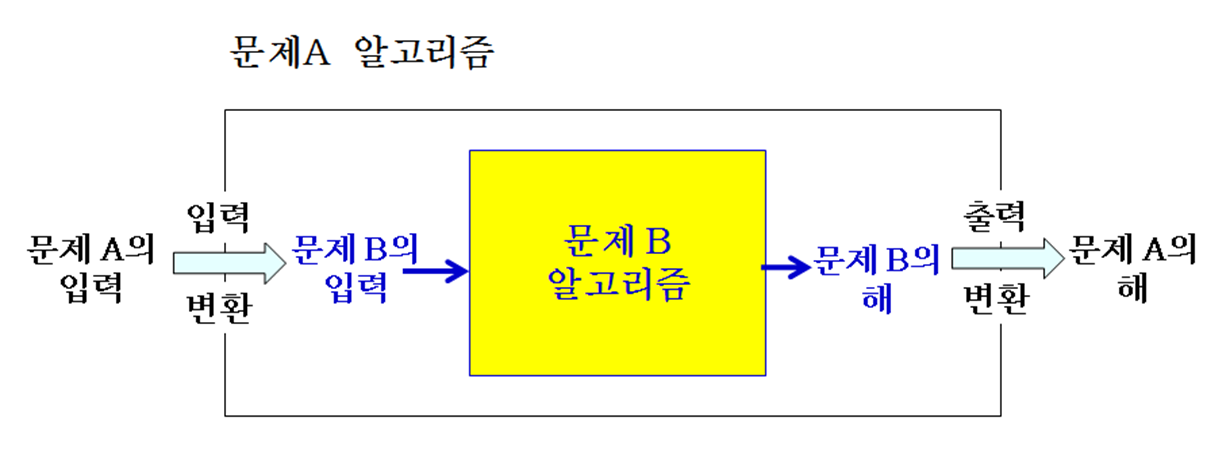
문제의 변환과 환원

문제의 변환

• 문제 A를 해결하기 위해서 문제 B를 해결하는 알고리즘을 이용하는 것

문제 변환 과정

• 문제 A의 입력을 문제 B의 입력 형태로 변환
• 변환된 입력으로 문제 B를 해결하는 알고리즘 수행
• 수행 결과인 해를 문제 A의 해로 변환
  

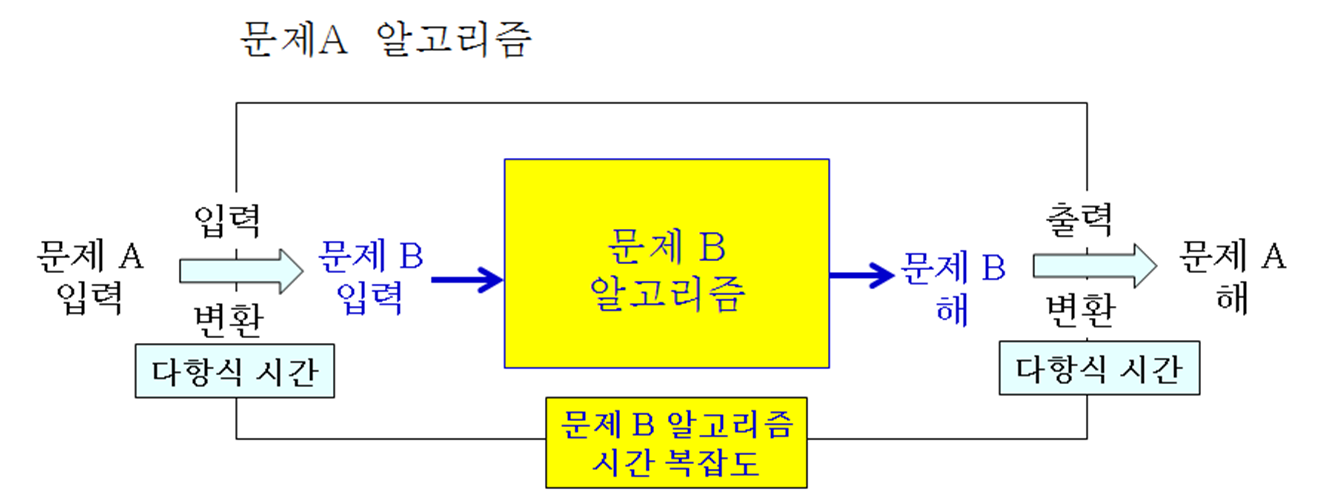
문제 변환 시간복잡도

• 문제 A의 입력을 문제 B의 입력으로 변환하는 시간
  • 다항식 시간
• 문제 B를 위한 알고리즘이 수행되는 시간
  • 이 단계의 시간 복잡도에 따라 결정
  • 다항식 시간 걸리면, 문제 A도 다항식 시간에 해결됨
• 문제 B의 해를 문제 A의 해로 변환하는 시간
  • 다항식 시간

NP-완전 문제 특성

추이 관계

• A -> B -> C,
  • A -> C
• NP-완전 문제들 중에서 어느 한 문제만 다항식 시간에 해결되면, 모든 다른 NP-완전 문제들이 다항식 시간에 해결됨!

NP-하드 문제 집합

NP-하드 문제

• 어느 문제 A에 대해서, 만일 모든 NP 문제가 문제 A로 다항식 시간에 변환이 가능할 때, 문제 A

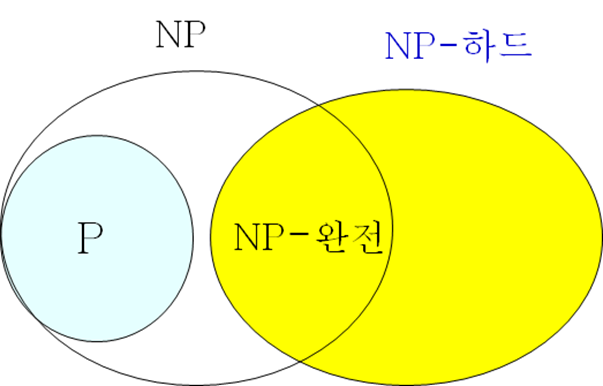
문제 집합 사이 관계

• NP-완전 문제는 NP-하드 문제이면서 NP 문제
  

NP-완전 문제

문제 A가 NP-완전 문제가 되려면,

• 문제 A는 NP 문제
• 문제 A는 NP-하드 문제