Ch 08. 근사 알고리즘 (1)

8.0 근사 알고리즘?

NP-완전 문제의 문제점

• 다항식 시간에 해결할 수 있는 알고리즘이 아직 발견되지 않음
• 다항식 시간에 해결할 수 없다고 증명하지 못함

NP-완전 문제 해결 조건

• NP-완전 문제들을 해결하려면 3가지 중에서 1가지는 포기해야 함
  • 다항식 시간에 해를 찾는 것
  • 모든 입력에 대해 해를 찾는 것
  • 최적해를 찾는 것

근사 알고리즘

• 최적해 찾기 포기!
• 최적해에 아주 근사한(가까운) 해를 찾아주는 것
• 근사 비율과 함께 제시

근사 비율

• 근사해의 값과 최적해의 값의 비율

• 1.0에 가까울수록 정확도가 높은 알고리즘

  • 1.0 -> 최적해

• 근사 비율을 계산하려면 최적해를 알아야 하는 모순 발생

• 최적해를 대신할 수 있는 ‘간접적인’ 최적해를 찾고, 이를 최적해로 삼아서 근사 비율을 계산!

8.1 여행자 문제

여행자 문제란?

• 임의의 한 도시에서 출발 -> 다른 모든 도시를 1번씩만 방문 -> 다시 출발했던 도시로 돌아오는 여행 경로의 길이를 최소화하는 문제

여행자 문제 조건

• 대칭성
  • A-B 거리 == B-A 거리
• 삼각 부등식 특성
  • A->B 거리 < A->C->B 거리

최소신장트리(MST) 이용

• 근사 알고리즘을 고안하기 위해서는, 먼저 다항식 시간 알고리즘을 가지면서 유사한 특성을 가진 문제를 찾아서 활용

과정

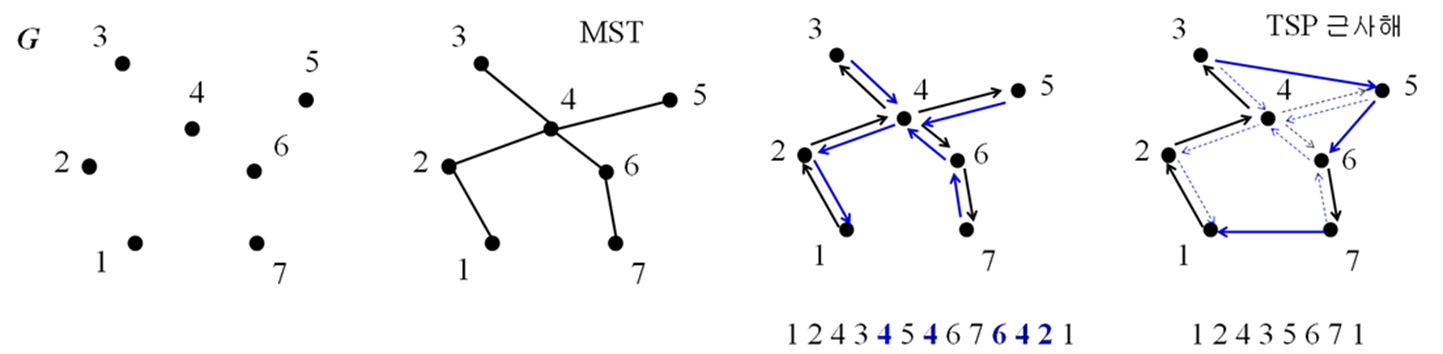
1. 최소신장트리 찾기(크루스칼, 프림)

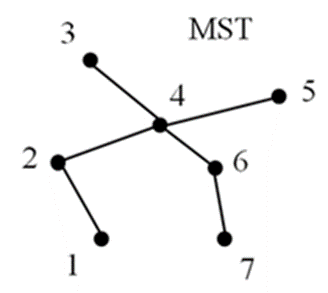
2. 도시 방문 순서 구하기
   

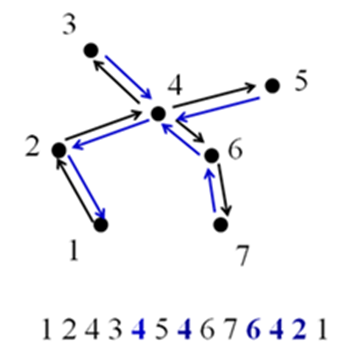
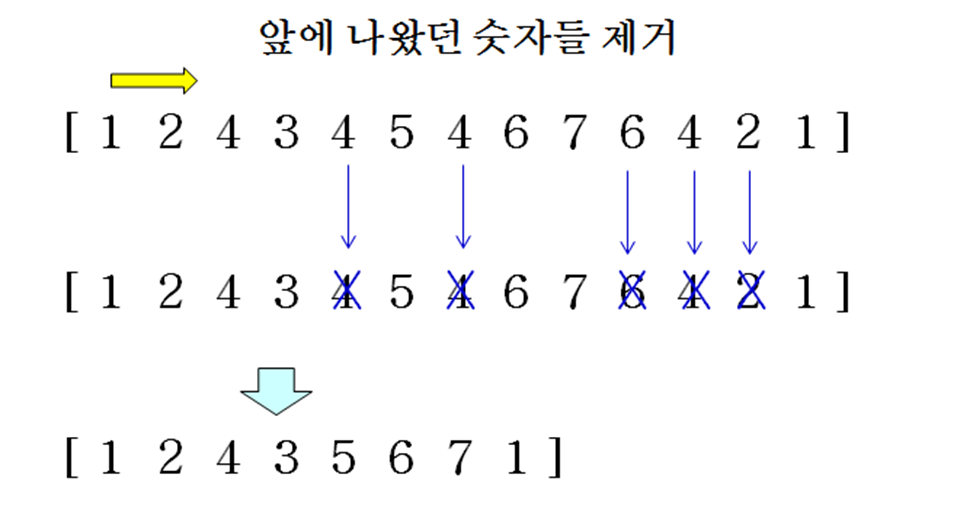
3. 중복 제거하기(삼각 부등식 특성 이용)
   

의사코드

• 입력: n개의 도시, 각 도시간의 거리
• 출력: 여행자 도시 순서

Approx_MST_TSP(){
	MST 찾기;
    방문 순서 구하기;
    중복 제거하기;
    return 도시 순서
}

시간복잡도

• MST 찾는 시간복잡도 + O(n) + O(n) = MST 시간복잡도
• MST 시간복잡도
  • 크루스컬: $O(mlogm)$
  • 프림: $O(n^2)$

근사 비율

• $2M/M=2$

8.2 정점 커버 문제

정점 커버 문제란?

• 그래프 G에서 각 선분의 양 끝점들 중, 적어도 하나의 끝점을 포함하는 점들의 집합들 중에서 최소 크기의 집합을 찾는 문제
• 정점 커버에 속한 점으로서 그래프의 모든 선분을 커버하는 것이다.
• 정점 커버를 찾는 것
  • 건물 내부 경비를 위한 최소의 카메라 수(정점 개수)와 각 카메라의 위치를 구하는 것과 동일하다.

과정(선분 선택 방법)

• 선택된 선분의 양 끝점에 인접한 선분 모두 커버
• 정점 커버: 선택된 각 선분의 양 끝점들의 집합
• 정점 커버를 형성 시, 새 선분은 자신의 양 끝점들이 이미 선택된 선분의 양 끝점들의 집합에 포함되지 않을 때에만 선택됨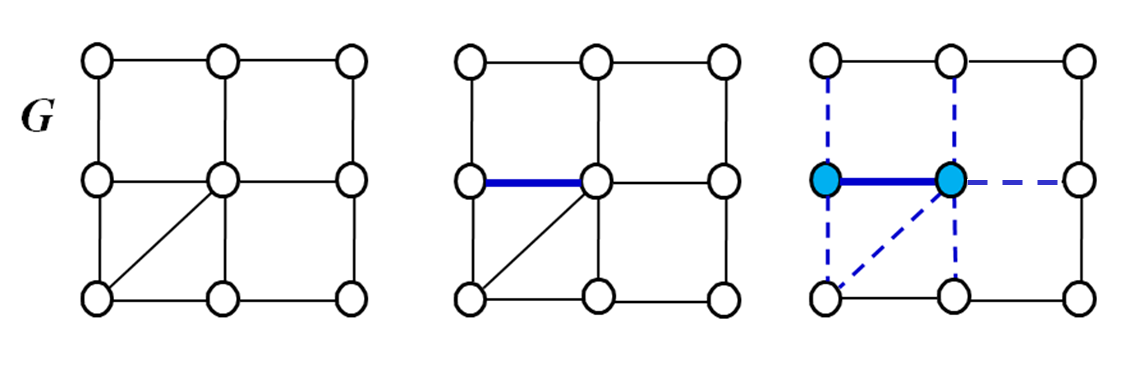

  

  • 선택된 선분의 양 끝점 (파란색 점)들이 점선으로 표시된 선분을 모두 커버하므로, 점선 선분은 이후에 정점 커버 선분으로 선택되지 않음
  • 이렇게 계속 선택될 선분이 없을 때까지 반복

극대 매칭

• 이미 선택된 선분에 기반을 두고 새로운 선분을 추가하려 해도 더 이상 추가할 수 없는 매칭
• 매칭
  • 각 선분의 양쪽 끝점들이 중복되지 않는 선분의 집합

의사코드

입력: 그래프 G=(V,E)
출력: 정점 커버

Approx_Matching_VC(G){
	입력 그래프에서 극대 매칭 M을 찾기;
	return 매칭 M의 선분의 양 끝점들의 집합;
}

시간복잡도

• 극대 매칭 찾는 시간복잡도
• $O(nm)$

근사 비율

• 극대 매칭 간접적인 최적해로 사용
  • 매칭에 있는 선분의 수를 최적해의 값으로 사용
• 근사해의 값 = 극대 매칭 선분 수 * 2
• 근사 비율
  • (극대 매칭의 각 선분의 양 끝점들의 수)/(극대 매칭의 선분 수) = 2