새싹 인공지능 응용sw 개발자 양성 교육 프로그램 심선조 강사님 수업 정리 글입니다.
회귀
-
교재 308P
-
입력값(=독립변수, feature, 피처),
입력변수들 사이에 관계성이 있다면 다중공선성문제라고 한다. -
결과값(=종속변수)
독립변수의 변화에 영향을 받아서 종속변수라고 한다.
상관관계분석 할 때 1, -1쪽으로 가까운 쪽의 결과가 나오면
1 : 하나가 오를 때 다른 값도 오름
-1 : 하나가 내려갈 때 다른 값도 내려감
독립변수가 값이 작아지면 종속변수도 영향을 받아서 값이 같이 작아지거나 커지거나
y = wx + b
y,x의 값은 우리가 안다.
y = w0 x0 + w1 x1 + w2 * x2 + b
x = 독립변수 w = 가중치(회귀 계수) y = 아파트 가격
회귀 예측의 핵심은 최적의 회귀 계수를 찾아내는 것
선형 회귀는 실제 값과 예측 값의 차이(오류의 제곱 값)을 최소화하는 직선형 회귀선을 최적화하는 방식이다.
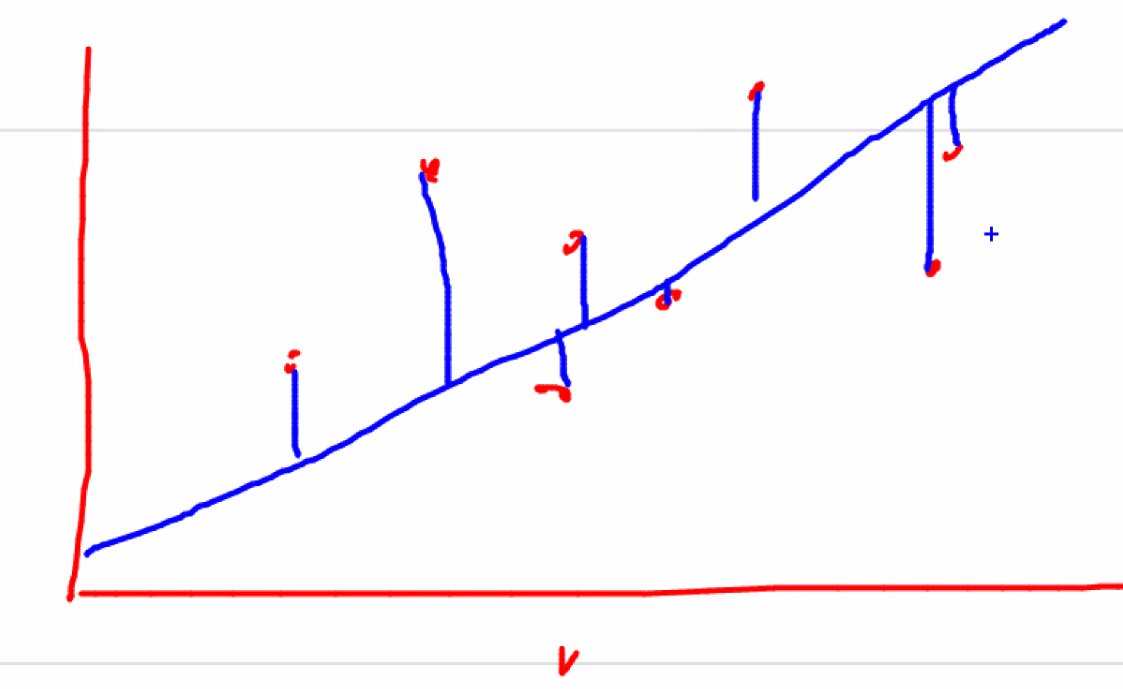
파랑색 선을 찾는 것
오차는 데이터 갯수만큼 나오니까 대표값 하나로 얘기한다.
대표값 하나가 차이값들을 전부다 더해서 평균값을 내는 것이다.
-없애주기 위해서 절대값, 제곱을 하거나
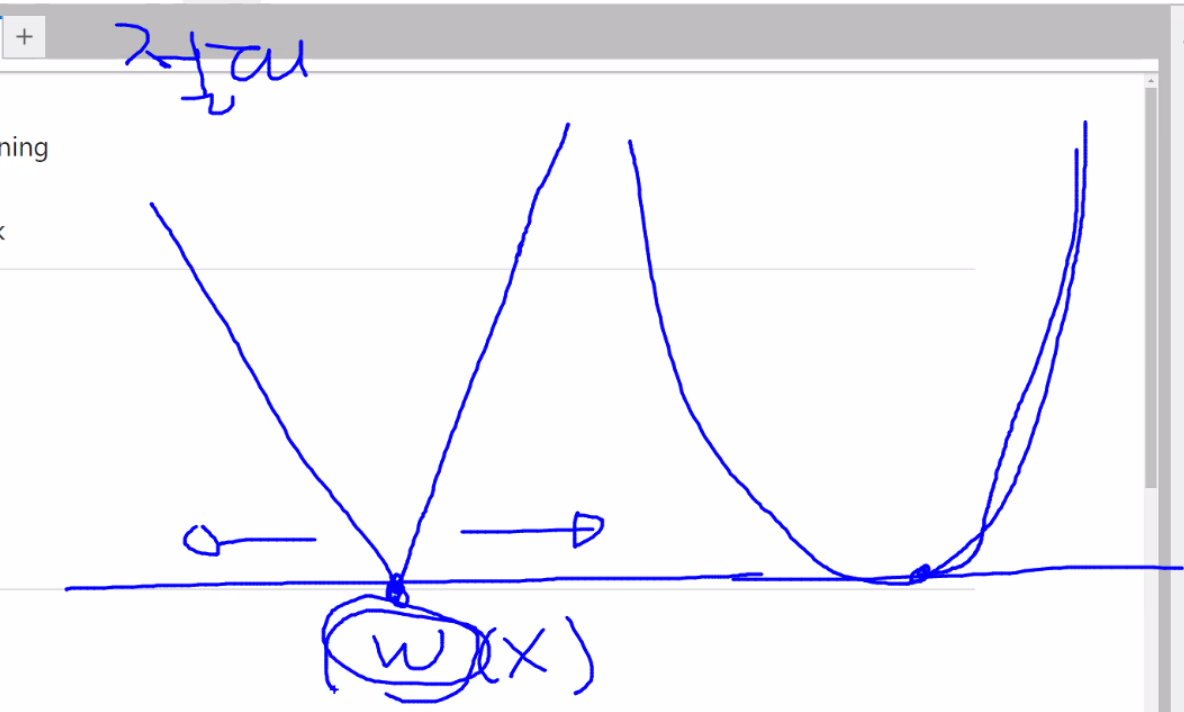
오차함수
임의로 W값 지정
학습률을 곱해서 이동할 간격이 나온다.
W(X)로 가는 것이 목표다.
선형회귀 모델은 규제 방법에 따라 다시 별도의 유형으로 나눌 수 있다.
회귀 계수에 패널티값을 더한다.
- 일반 선형 회귀
- 릿지 : 선형 회귀에 L1규제를 적용한 방식
- 라쏘 : L1 규제에 적용한 방식, L
- 엘라스틱넷 : L2,L1 규제를 함께 결합한 모델
- 로지스틱 회귀
회귀 계수가 0이 된다면 feature가 탈락한다. 영향력이 없다.
-
교재 312P
-
비용함수
1/N = 평균을 구한다.
Y = 실제값
x,w = 예측값 -
경사하강법
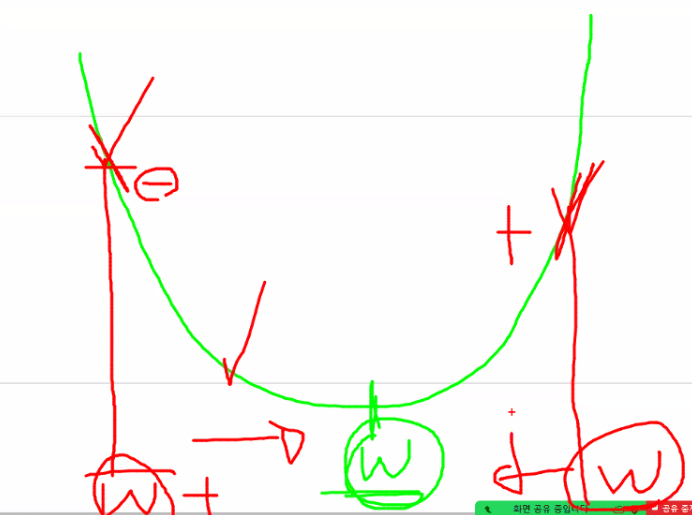
# 교재 315p
import numpy as np
import matplotlib.pyplot as pltnp.random.seed(0)X = 2 * np.random.rand(100,1) #shape 100 행 1열 총 데이터 갯수 100개
Xarray([[1.09762701],
[1.43037873],
[1.20552675],
[1.08976637],
[0.8473096 ],
[1.29178823],
[0.87517442],
[1.783546 ],
[1.92732552],
[0.76688304],
[1.58345008],
[1.05778984],
[1.13608912],
[1.85119328],
[0.14207212],
[0.1742586 ],
[0.04043679],
[1.66523969],
[1.5563135 ],
[1.7400243 ],
[1.95723668],
[1.59831713],
[0.92295872],
[1.56105835],
[0.23654885],
[1.27984204],
[0.28670657],
[1.88933783],
[1.04369664],
[0.82932388],
[0.52911122],
[1.54846738],
[0.91230066],
[1.1368679 ],
[0.0375796 ],
[1.23527099],
[1.22419145],
[1.23386799],
[1.88749616],
[1.3636406 ],
[0.7190158 ],
[0.87406391],
[1.39526239],
[0.12045094],
[1.33353343],
[1.34127574],
[0.42076512],
[0.2578526 ],
[0.6308567 ],
[0.72742154],
[1.14039354],
[0.87720303],
[1.97674768],
[0.20408962],
[0.41775351],
[0.32261904],
[1.30621665],
[0.50658321],
[0.93262155],
[0.48885118],
[0.31793917],
[0.22075028],
[1.31265918],
[0.2763659 ],
[0.39316472],
[0.73745034],
[1.64198646],
[0.19420255],
[1.67588981],
[0.19219682],
[1.95291893],
[0.9373024 ],
[1.95352218],
[1.20969104],
[1.47852716],
[0.07837558],
[0.56561393],
[0.24039312],
[0.5922804 ],
[0.23745544],
[0.63596636],
[0.82852599],
[0.12829499],
[1.38494424],
[1.13320291],
[0.53077898],
[1.04649611],
[0.18788102],
[1.15189299],
[1.8585924 ],
[0.6371379 ],
[1.33482076],
[0.26359572],
[1.43265441],
[0.57881219],
[0.36638272],
[1.17302587],
[0.04021509],
[1.65788006],
[0.00939095]])np.random.randint() : 균일 분포의 정수 난수 1개 생성
np.random.rand() 0부터 1사이의 균일 분포에서 난수 matrix array생성
np.random.randn() 가우시안 표준 정규 분포에서 난수 matrix array생성
- 가우시안 정규분포
평균근처가 제일 많고 평균에서 멀어질 수록 줄어든다.
y = 6 + 4 * X + np.random.randn(100, 1) #np.random.randn(100, 1) = 노이즈plt.scatter(X,y)<matplotlib.collections.PathCollection at 0x2c68f0489a0>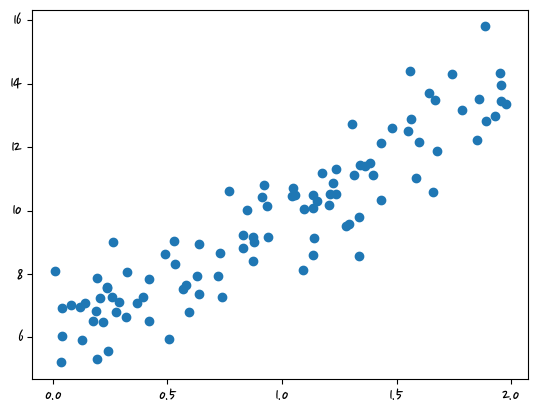
- 교재 316p 오타
N = LEN(y) 들여써야 함
y = 정답, y.pred = 예측값
w0 = b
def get_weight_updates(w1,w0,X,y,learning_rate=0.01): #w1 = 가중치, w0 = b
N = len(y)
w1_update = np.zeros_like(w1) #파리미터(w1)와 같은 형태 안에 0으로 채워서 만들어라
w1_update = np.zeros_like(w0)
y_pred = np.dot(X,w1.T)+w0 #예측, dot=행렬곱, X(뒤의 컬럼수)*w1(앞의 행) 일치해야 계산 가능 , .T = transpose # y = x,w+b와 비슷
diff = y-y_pred
w0_factors = np.ones((N,1))
w1_update = -(2/N)*learning_rate*(np.dot(X.T,diff)) #w1편미분
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T,diff)) #w0편미분
return w1_update,w0_updatedef gradient_descent_steps(X,y,iters=10000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
for ind in range(iters):
w1_update,w0_update = get_weight_updates(w1,w0,X,y)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1,w0def get_cost(y,y_pred):
N = len(y)
cost = np.sum(np.square(y-y_pred))/N
return costw1,w0 = gradient_descent_steps(X,y,iters=1000)print(w1,w0)[[3.94408465]] [[5.89269511]]
y_pred = w1[0,0]*X+w0 #0행에 0번째 값
get_cost(y,y_pred)0.959586122614184- 행렬곱
사이킷런 LinearRegression을 이용한 보스턴 주택 가격 예측
- 교재 312p
b는 0으로 두고 계산 안 하기도 한다. 뭐랑 같은지?
LinearRegression 클래스는 fit() 메서드로 X,y배열을 입력받으면 회귀 계수(Coeffi)인 w값을 coef_에 저장한다.
피저간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해진다.
이러한 현상을 다중공선성문제라고 한다.
매우 많은 경우 pca(신용카드할 때 나옴)를 통해 차원 축소를 수행
회귀 평가 지표
회귀는 연속된 데이터라서 연속값은 맞춘다는 개념보다는 오차와 실제값사이가 오차가 얼마나 작게 나는 지
-
MAE : 실제값과 예측값의 차이를 절댓값으로 변환해 평균한 것
-
MSE : 실제값과 예측값의 차이를 제곱으로 변환해 평균한 것
-
RMSE : 루트를 씌운것
-
R^2 : 실제값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 예측 정확도가 높다.
-
사이킷런 평가 지표 API
어제 *-1한 것 =
분산이 둘 다 같으면 1이 된다. 1이 되면 좋다
- 교재 362p
회귀 실습 - 자전거 대여 수요 예측
https://www.kaggle.com/competitions/bike-sharing-demand/overview/description
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')df = pd.read_csv('bike.csv')
df.head(2)| datetime | season | holiday | workingday | weather | temp | atemp | humidity | windspeed | casual | registered | count | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2011-01-01 00:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 81 | 0.0 | 3 | 13 | 16 |
| 1 | 2011-01-01 01:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0 | 8 | 32 | 40 |
df.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10886 entries, 0 to 10885
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 datetime 10886 non-null object
1 season 10886 non-null int64
2 holiday 10886 non-null int64
3 workingday 10886 non-null int64
4 weather 10886 non-null int64
5 temp 10886 non-null float64
6 atemp 10886 non-null float64
7 humidity 10886 non-null int64
8 windspeed 10886 non-null float64
9 casual 10886 non-null int64
10 registered 10886 non-null int64
11 count 10886 non-null int64
dtypes: float64(3), int64(8), object(1)
memory usage: 1020.7+ KB#object형 -> 날짜형
df['datetime'] = df.datetime.apply(pd.to_datetime) #apply()=함수적용 , dtype: datetime64[ns] = 데이터 타입 날짜형으로 바뀜df.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10886 entries, 0 to 10885
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 datetime 10886 non-null datetime64[ns]
1 season 10886 non-null int64
2 holiday 10886 non-null int64
3 workingday 10886 non-null int64
4 weather 10886 non-null int64
5 temp 10886 non-null float64
6 atemp 10886 non-null float64
7 humidity 10886 non-null int64
8 windspeed 10886 non-null float64
9 casual 10886 non-null int64
10 registered 10886 non-null int64
11 count 10886 non-null int64
dtypes: datetime64[ns](1), float64(3), int64(8)
memory usage: 1020.7 KBdf['year'] = df.datetime.apply(lambda x:x.year) #연도 추출
df['month'] = df.datetime.apply(lambda x:x.month)
df['day'] = df.datetime.apply(lambda x:x.day)
df['hour'] = df.datetime.apply(lambda x:x.hour) df.head(2)| datetime | season | holiday | workingday | weather | temp | atemp | humidity | windspeed | casual | registered | count | year | month | day | hour | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2011-01-01 00:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 81 | 0.0 | 3 | 13 | 16 | 2011 | 1 | 1 | 0 |
| 1 | 2011-01-01 01:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0 | 8 | 32 | 40 | 2011 | 1 | 1 | 1 |
#count값 예상하고 자 하는 값, 회원 + 비회원 = count, 예측하고 자 하는 값이 독립변수안에 들어가 있음
df.drop(columns=['datetime','casual','registered'],inplace=True)오버플로, 언더플로 오류가 발생하기 쉽다
- 교재368p
log1p = 1+log()
원래값으로 복원이 된다.
log1p처리 된 데이터는 expm1()함수사용하면 원래값으로 복원된다.
로그 변환, 피처 인코드이과 모델 학습/예측/평가
-
교재 369p
회귀는 정규분포 형태인지 확인하는 것이 중요하다
결과(target)값의 분포를 확인하는 것이 중요하다. -> 히스토그램
정규분포로 변환 log1p()로 정규분포 형태로 전환. 그 중 효과가 좋은 것이 log1p()다
개별 피처 인코딩 (원핫인코딩, 레이블인코딩)
회귀계수가 크다는 것은 영향력이 크다. 숫자커서 회귀계수가 크다. -> 원핫인코딩 이용
원핫인코딩 후 평가 수행하고 결과값 확인, minmax도 사용가능 -
정리
회귀는 타켓값의 분포가 중요하다.
숫자값의 크기에 따라 영향을 받기 때문에 레이블 인코딩이 필요하다.
