문제
수식은 일반적으로 3가지 표기법으로 표현할 수 있다. 연산자가 피연산자 가운데 위치하는 중위 표기법(일반적으로 우리가 쓰는 방법이다), 연산자가 피연산자 앞에 위치하는 전위 표기법(prefix notation), 연산자가 피연산자 뒤에 위치하는 후위 표기법(postfix notation)이 그것이다. 예를 들어 중위 표기법으로 표현된 a+b는 전위 표기법으로는 +ab이고, 후위 표기법으로는 ab+가 된다.
이 문제에서 우리가 다룰 표기법은 후위 표기법이다. 후위 표기법은 위에서 말한 법과 같이 연산자가 피연산자 뒤에 위치하는 방법이다. 이 방법의 장점은 다음과 같다. 우리가 흔히 쓰는 중위 표기식 같은 경우에는 덧셈과 곱셈의 우선순위에 차이가 있어 왼쪽부터 차례로 계산할 수 없지만 후위 표기식을 사용하면 순서를 적절히 조절하여 순서를 정해줄 수 있다. 또한 같은 방법으로 괄호 등도 필요 없게 된다. 예를 들어 a+bc를 후위 표기식으로 바꾸면 abc+가 된다.
중위 표기식을 후위 표기식으로 바꾸는 방법을 간단히 설명하면 이렇다. 우선 주어진 중위 표기식을 연산자의 우선순위에 따라 괄호로 묶어준다. 그런 다음에 괄호 안의 연산자를 괄호의 오른쪽으로 옮겨주면 된다.
예를 들어 a+bc는 (a+(bc))의 식과 같게 된다. 그 다음에 안에 있는 괄호의 연산자 를 괄호 밖으로 꺼내게 되면 (a+bc)가 된다. 마지막으로 또 +를 괄호의 오른쪽으로 고치면 abc*+가 되게 된다.
다른 예를 들어 그림으로 표현하면 A+B*C-D/E를 완전하게 괄호로 묶고 연산자를 이동시킬 장소를 표시하면 다음과 같이 된다.
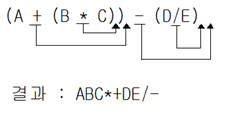
이러한 사실을 알고 중위 표기식이 주어졌을 때 후위 표기식으로 고치는 프로그램을 작성하시오
입력
첫째 줄에 중위 표기식이 주어진다. 단 이 수식의 피연산자는 A~Z의 문자로 이루어지며 수식에서 한 번씩만 등장한다. 그리고 -A+B와 같이 -가 가장 앞에 오거나 AB와 같이 가 생략되는 등의 수식은 주어지지 않는다. 표기식은 알파벳 대문자와 +, -, , /, (, )로만 이루어져 있으며, 길이는 100을 넘지 않는다.
A*(B+C)출력
첫째 줄에 후위 표기식으로 바뀐 식을 출력하시오
ABC+*
접근 방식

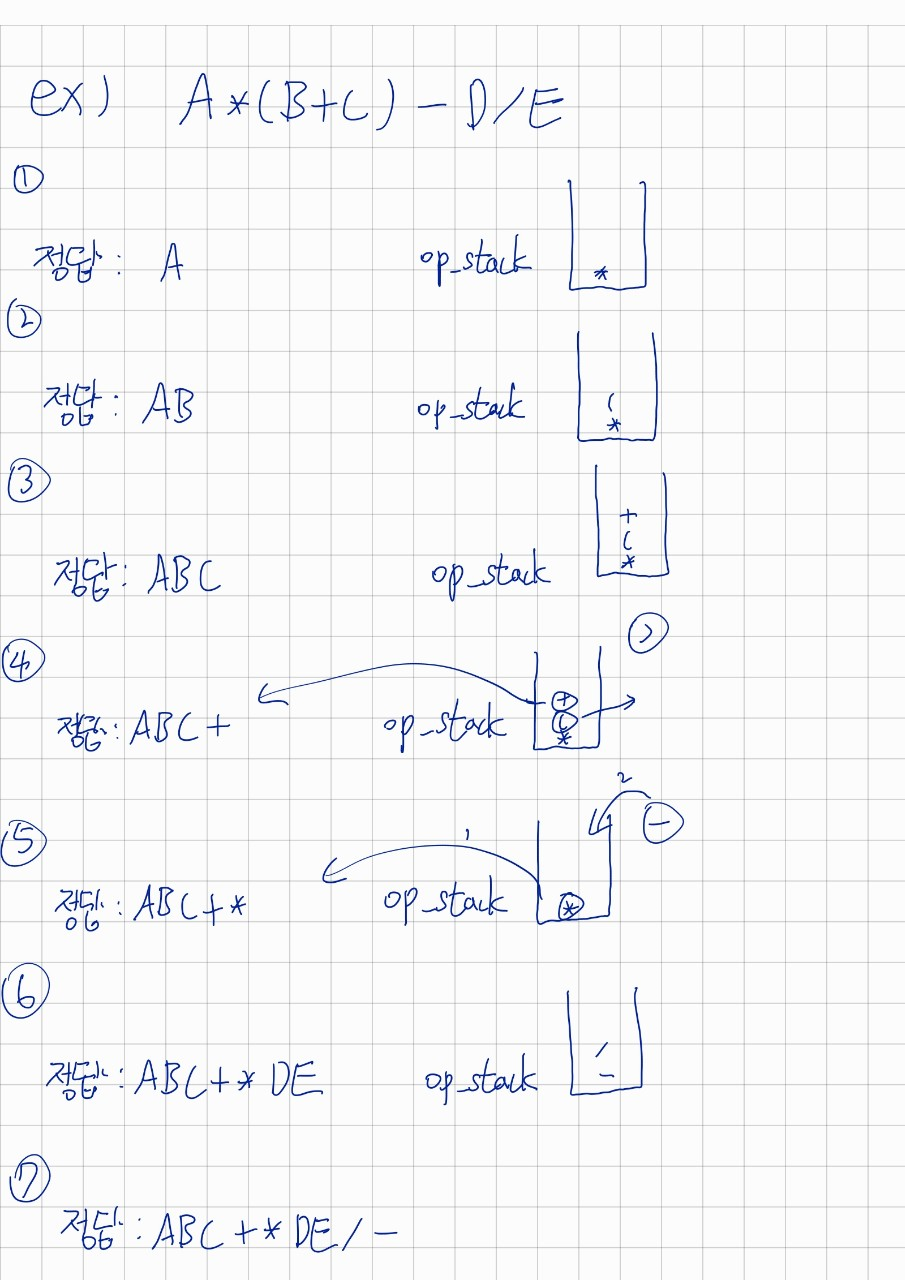
코드
strs = input()
# 연산자 스택
op_stack = []
# 정답
answer = ''
for char in strs:
# 알파벳이면 바로 정답 문자열에 추가
if char.isalpha():
answer += char
# 연산자 계산
else:
# 왼쪽괄호는 바로 연산자 스택에 추가
if char == '(':
op_stack.append(char)
# 곱셈과 나눗셈은 같은 우선순위인 연산자를 연산자 스택에서 정답 문자열로 옮긴 후 추가
elif char == '*' or char == '/':
while len(op_stack) != 0 and op_stack[-1] in ['*','/']:
answer += op_stack.pop()
op_stack.append(char)
# 덧셈과 뺄셈은 왼쪽 괄호를 만나거나 스택이 빌 때까지 모두 정답 문자열로 옮긴 후 추가
elif char == '+' or char == '-':
while len(op_stack) != 0 and op_stack[-1] != '(':
answer += op_stack.pop()
op_stack.append(char)
# 오른쪽 괄호는 왼쪽 괄호를 만날 때까지 정답 문자열로 옮긴 후 왼쪽 괄호 제거
else : # char == ')'
while op_stack[-1] != '(':
answer += op_stack.pop()
op_stack.pop()
while len(op_stack) != 0:
answer += op_stack.pop()
print(answer)

