[알고리즘] Java / 백준 / 볼록 껍질 / 1708

[알고리즘] Java / 백준 / 볼록 껍질 / 1708

문제

문제 링크

접근 방식

convex hull 문제 풀이 순서

1. 루트 정점 정하기
2. 루트 정점을 기준으로 반시계 방향 정렬하기(ccw활용)
3. 스택에 루트 정점을 넣고 정렬한 정점 리스트를 탐색
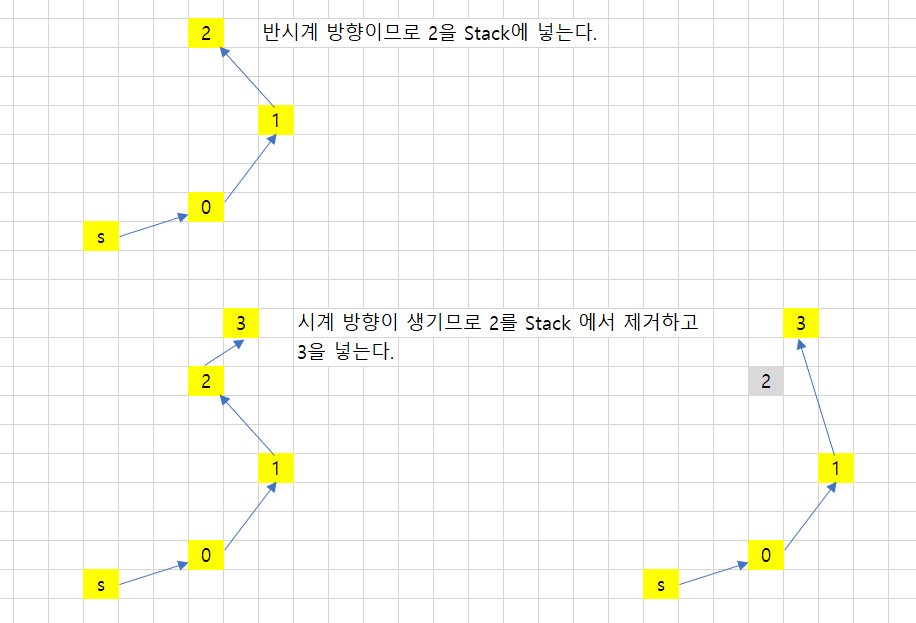
4. 스택입구의 두 번째 점, 첫 번째 점, 탐색한 정점으로 ccw를 구하고 해당 값이 반시계 방향이면 탐색한 정점을 스택에 넣는다.
5. ccw 값이 반시계 방향이 아니라면 stack의 첫 번째 점을 pop하고 다시 4번으로 간다.
6. 최종적으로 남은 스택의 크기를 출력한다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Stack;
import java.util.StringTokenizer;

public class Main_1708 {

	public static class Point{
		long x;
		long y;
		Point(long x, long y){
			this.x = x;
			this.y = y;
		}

	}
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		
		StringTokenizer st = null;
		
		List<Point> pointList = new ArrayList<>();
		for(int i=0;i<N;i++) {
			st = new StringTokenizer(br.readLine());
			int x = Integer.parseInt(st.nextToken());
			int y = Integer.parseInt(st.nextToken());
			pointList.add(new Point(x,y));
		}
		
		System.out.println(grahamScan(pointList));
	}
	static Point root;
	public static int grahamScan(List<Point> pointList) {
		// root 찾기
		root = new Point(Long.MAX_VALUE,Long.MAX_VALUE);
		
		for(int i=0;i<pointList.size();i++) {
			Point nowPoint  = pointList.get(i);
			if(nowPoint.y < root.y) {
				root = nowPoint;
			}else if(nowPoint.y == root.y) {
				if(nowPoint.x < root.x) {
					root = nowPoint;
				}
			}
		}
		
		// 모든 점을 root기준 반시계 방향으로 정렬하기
		pointList.sort(new Comparator<Point>(){
			@Override
			public int compare(Point p1, Point p2) {
				long result = ccw(root,p1,p2);
				if(result > 0) {
					return -1;
				} else if(result < 0) {
					return 1;
				} else if(dist(root, p1) > dist(root,p2)){
					return 1;
				}
				return -1;
			}
		});
		
		Stack<Point> stack = new Stack<>();
		stack.add(root);
		
		for(int i=1;i<pointList.size();i++) {
			
			while(stack.size() > 1 && ccw(stack.get(stack.size()-2), stack.get(stack.size()-1),pointList.get(i)) <= 0){
				stack.pop();
			}
			stack.add(pointList.get(i));
		}
		return stack.size();
	}
	
	public static long ccw(Point p1, Point p2, Point p3) {
		return p1.x*p2.y + p2.x*p3.y + p3.x*p1.y - (p1.y*p2.x + p2.y*p3.x + p3.y*p1.x); 
	}
	
	public static long dist(Point p1, Point p2) {
		return (long)(Math.pow(p2.x - p1.x,2) + Math.pow(p2.y - p1.y, 2));
	}

}