그래프 신경망 - 심화

ganta·2021년 2월 27일

Graph

Graph 이론

목록 보기

9/9

그래프 신경망에서의 어텐션

기본 그래프 신경망의 한계
✔️ 기본 그래프 신경망에서는 이웃들의 정보를 동일한 가중치의 평균으로 계산을 함
그래프 합성곱 신경망에서도 단순히 연결성을 고려한 가중치로 평균 계산
❗️ 현실에서는 이웃들이랑 모두 대등하게 연결되어 있지는 않음(예 - 더 친한 친구 vs 덜 친한 친구)
그래프 어텐션 신경망(Graph Attention Network, GAT)
✔️ 그래프 어텐션 신경망에서는 가중치 자체도 학습

✔️ 이웃 별로 미치는 영향이 다를 수 있기 때문에 가중치를 학습하기 위해 셀프-어텐션(Self-Attention)이 사용된다.

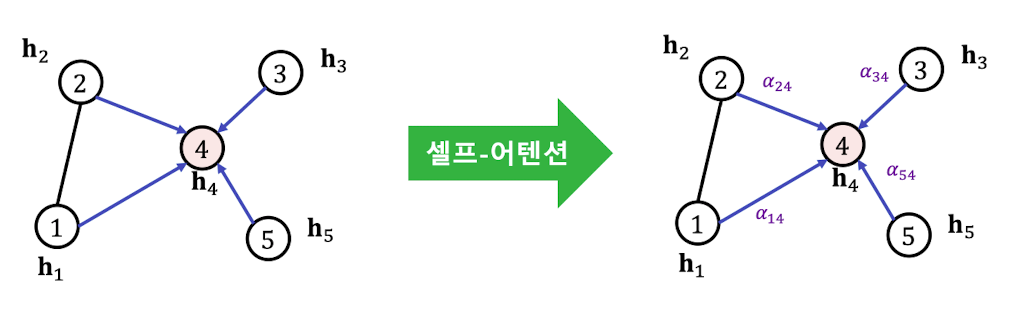
출처
Naver BoostCamp AI Tech - edwith 강의
http://snap.stanford.edu/proj/embeddings-www/

각 층에서 정점 $i$ 로부터 이웃 $j$ 로의 가중치 $\alpha_{ij}$ 는 세 단계를 통해 계산이 된다.
1️⃣ 해당 층의 정점 $i$ 의 임베딩 $h_i$ 에 신경망 $W$ 를 곱해 새로운 임베딩을 얻음
➡️ $\tilde{h_i} = h_iW$
(이때, $W$ 는 학습 변수이다.)
2️⃣ 정점 $i$ 와 정점 $j$ 의 새로운 임베딩을 연결한 후, 어텐션 계수 $a$ 를 내적한다.( $a$ 는 모든 정점이 공유하는 학습 변수)
➡️ $e_{ij} = a^{\top}[CONCAT(\tilde{h_i},\tilde{h_j})]$
(이때, $a$ 는 어텐션 계수이다.)
3️⃣ 2️⃣의 결과에 소프트맥스(Softmax)를 적용
➡️ $\alpha_{ij} = softmax_j(e_{ij}) = \frac{exp(e_{ij})}{\sum_{k \in N_i}exp(e_{ik})}$

여러 개의 어텐션을 동시에 학습한 뒤, 결과를 연셜하여 사용하는 멀티헤드 어텐션(Multi-head Attenteion)도 존재한다.

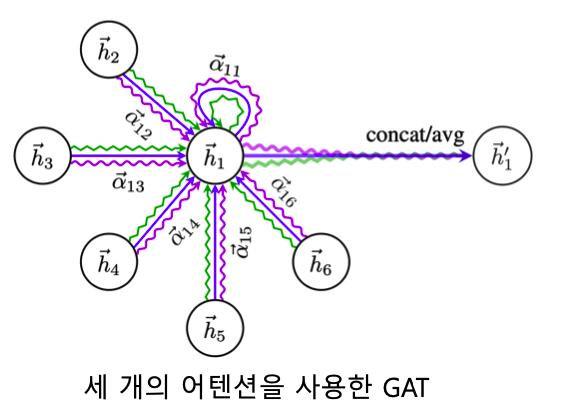
출처
Naver BoostCamp AI Tech - edwith 강의
https://arxiv.org/pdf/1710.10903.pdf

${h_i}' = CONCAT_{1 \leq k \leq K}\sigma(\sum_{j \in N_i}\alpha^k_{ij}h_jW_k)$

✔️ 어텐션의 결과 정점 분류의 정확도(Accuracy)가 향상

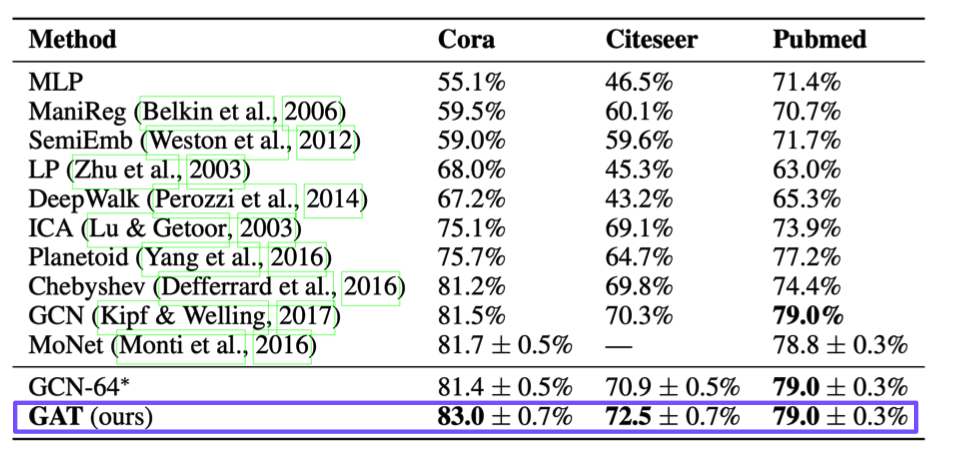
출처
Naver BoostCamp AI Tech - edwith 강의

그래프 표현 학습과 그래프 풀링

그래프 표현 학습이란?
✔️ 그래프 표현 학습(그래프 임베딩)이란 그래프 전체를 벡터의 형태로 표현하는 것이다.

👉 개별 정점을 벡터의 형태로 표현하는 정점 표현 학습과 구분된다. 그래프 임베딩은 벡터의 형태로 표현된 그래프 자체를 의미
👉 그래프 임베딩은 그래프 분류에 활용된다.(예 - 그래프 형태로 표현된 화합물의 분자 구조로부터 특성을 예측)
그래프 풀링(Graph Pooling)
✔️ 그래프 풀링(Graph Pooling)이란 정점 임베딩으로부터 그래프 임베딩을 얻는 과정이다.

👉 평균 등 단순한 방법보다 그래프의 구조를 고려한 방법을 사용한 경우 그래프 분류 등 후속 과제(Downstream Task)에서 더 높은 성능을 얻을 수 있다.
👉 해당 그림의 미분가능한 풀링(Differentiable Pooling, DiffPoll)은 군집 구조(=>활용 임베딩)를 계층적으로 집계(마지막으로는 classifier 통과)
이때, 그래프 신경망이 여러곳에서 사용이 되어진다.
1️⃣ 개별 정점의 임베딩을 얻을 때
2️⃣ 군집별로 묶어줄 때
3️⃣ 군집내에서 합산하는 방법 또한 그래프 신경망으로 결정

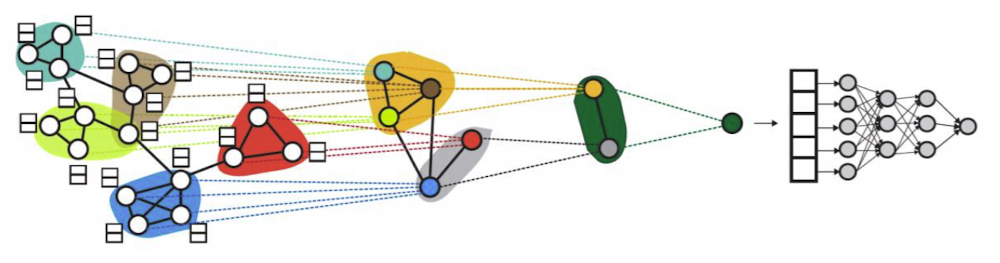
출처
Naver BoostCamp AI Tech - edwith 강의
https://arxiv.org/pdf/1806.08804.pdf

지나친 획일화 문제

지나친 획일화(Over-smoothing) 문제란?
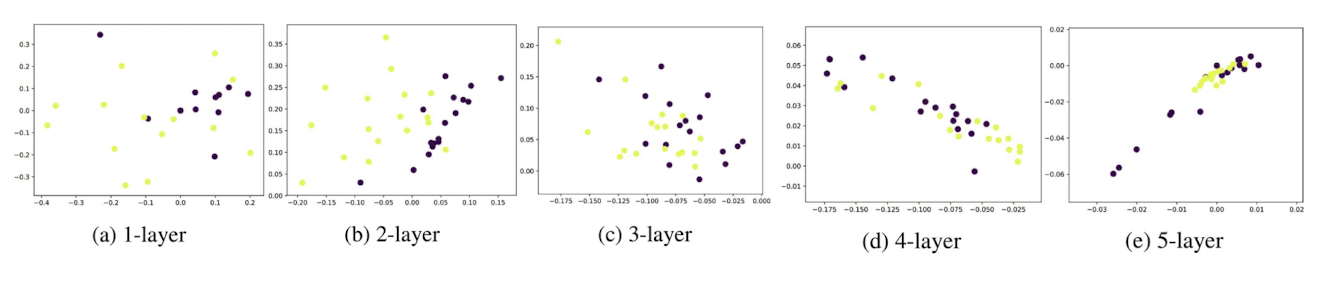
✔️ 지나친 획일화(Over-smoothing) 문제란 그래프 신경망의 층의 수가 증가하면서 정점의 임베딩이 서로 유사해지는 현상을 의미
👉 작은 세상 효과와 관련이 있다. 즉 적은 수의 층으로도 자수의 정점에 의해 영향을 받게 된다. (정점간 거리가 너무 가까워서 발생되는 문제)

출처
Naver BoostCamp AI Tech - edwith 강의
https://ojs.aaai.org/index.php/AAAI/article/view/11604

층을 너무 많이 통과하게 되면 정점들이 서로 너무 유사하게 되어버림
예시
➡️ 그래프 층 5개 통과 가정
➡️ 5만큼 떨어진 정점들의 정보를 집계
➡️ 많은 정점들의 거리가 가깝다 보니 수많은 정점들을 집계를 하고 정점을 보기 보다는 그래프 전반을 집계하는 효과가 발생하게 된다.
➡️ 정점들이 대부분 비슷비슷하게 임베딩이 되어지고 이에 따라 분류의 성능이 떨어지게 된다.

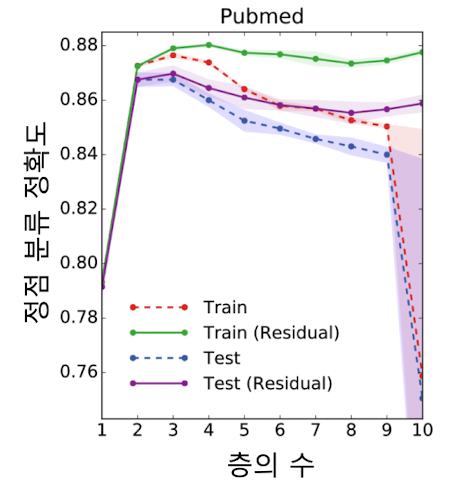
✔️ 지나친 획일화의 결과로 그래프 신경망의 층의 수를 늘렸을 때, 후속과제에서의 정확도가 감소하는 현상이 발생(신경망의 층이 2개 혹은 3개 일 때 가장 높음)
이때, 이를 보완하고자 잔차항(Residual)을 넣는 것(이전 층의 임베딩을 한 번 더 더해주는 것 $h_u^{(l + 1)} = h_u^{(l + 1)} + h_u^{(l)}$ 만으로는 제한된 효과를 보여주게 된다.

출처
Naver BoostCamp AI Tech - edwith 강의
지나친 획일화 문제에 대한 대응
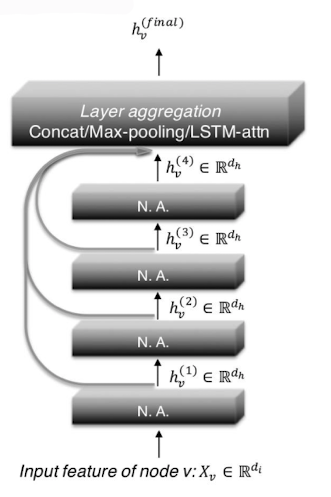
✔️ JK 네트워크(Jumping Knowledge Network)
마지막 층의 임베딩 뿐 아니라, 모든 층의 임베딩을 함께 사용

출처
Naver BoostCamp AI Tech - edwith 강의
https://arxiv.org/pdf/1806.03536.pdf

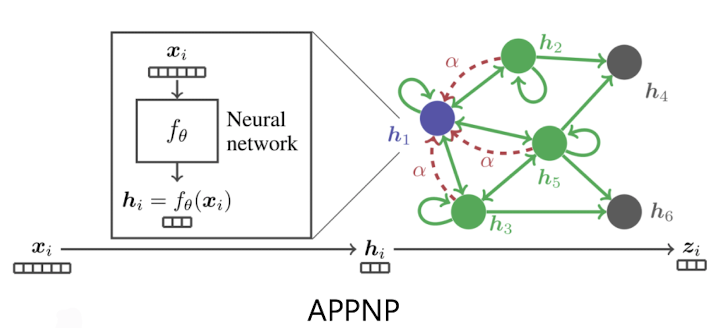
✔️ APPNP
0번째 층을 제외하고는 신경망 없이 집계 함수를 단순화(앞의 함수에서 집계 함수 $W$ 를 없애 버림)

출처
Naver BoostCamp AI Tech - edwith 강의
https://arxiv.org/pdf/1810.05997.pdf

후속 과제로써 정점 분류 문제를 하였을 때, APPNP의 경우, 층의 수 증가에 따른 정확도 감소 효과가 없었다.

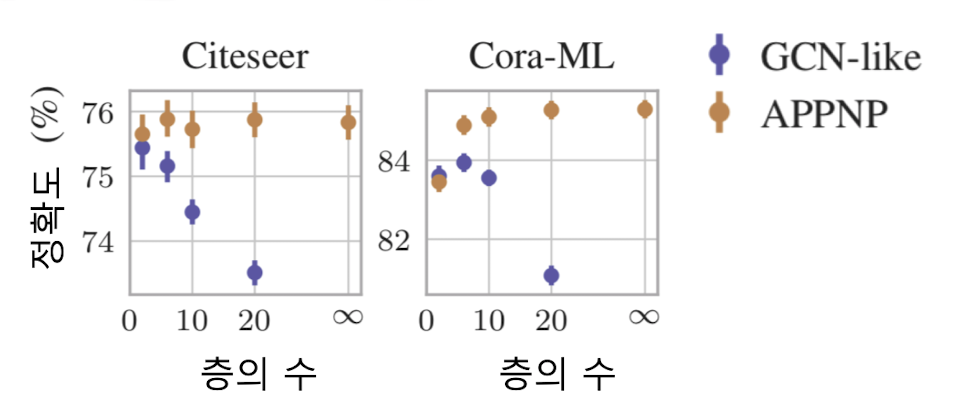
출처
Naver BoostCamp AI Tech - edwith 강의
https://arxiv.org/pdf/1810.05997.pdf

그래프 데이터 증강

데이터 증강(Data Augmentataion)
✔️ 데이터 증강(Data Augmentataion)은 데이터의 수를 증가시키는 것을 말하고 다양한 기계학습 문제에서 효과적이다.(특히 이미지에서 효과적)
👉 그래프에서도 누락되거나 부정확한 간선이 존재 할 수 있고, 데이터 증강을 통해 보완할 수 있다.
이에 따른 방법으로 임의 보행을 통해 정점간 유사도를 계산하고 유사도가 높은 정점 가느이 간선을 추가하는 방법이 제안되어짐

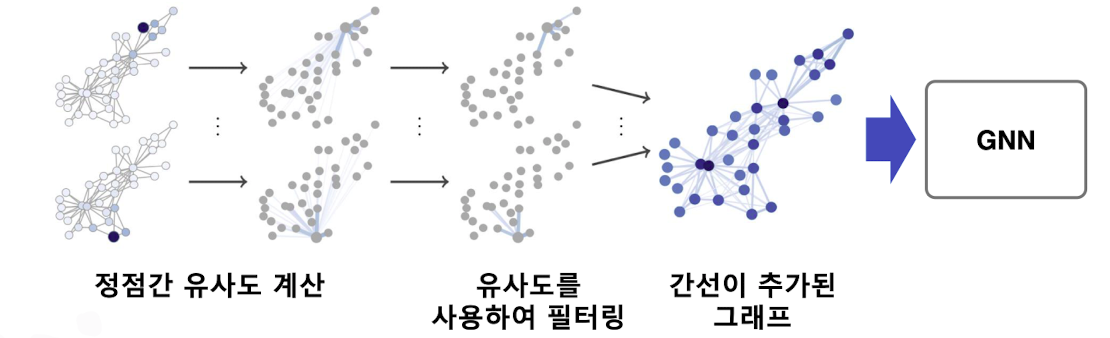
출처
Naver BoostCamp AI Tech - edwith 강의
https://arxiv.org/abs/1911.05485

이에 따라 정점분류의 정확도가 개선될 수 있다.

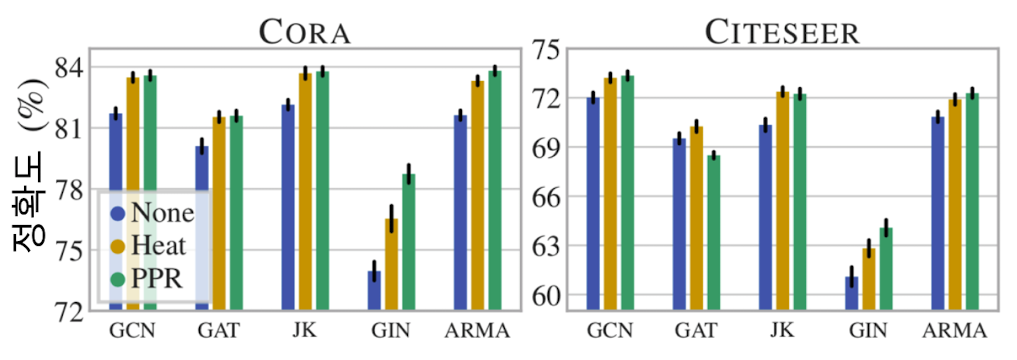
출처
Naver BoostCamp AI Tech - edwith 강의
https://arxiv.org/abs/1911.05485

이때, HEAT과 PPR은 제안된 그래프 데이터 증강 기법을 의미한다.