[프로그래머스] 단속카메라

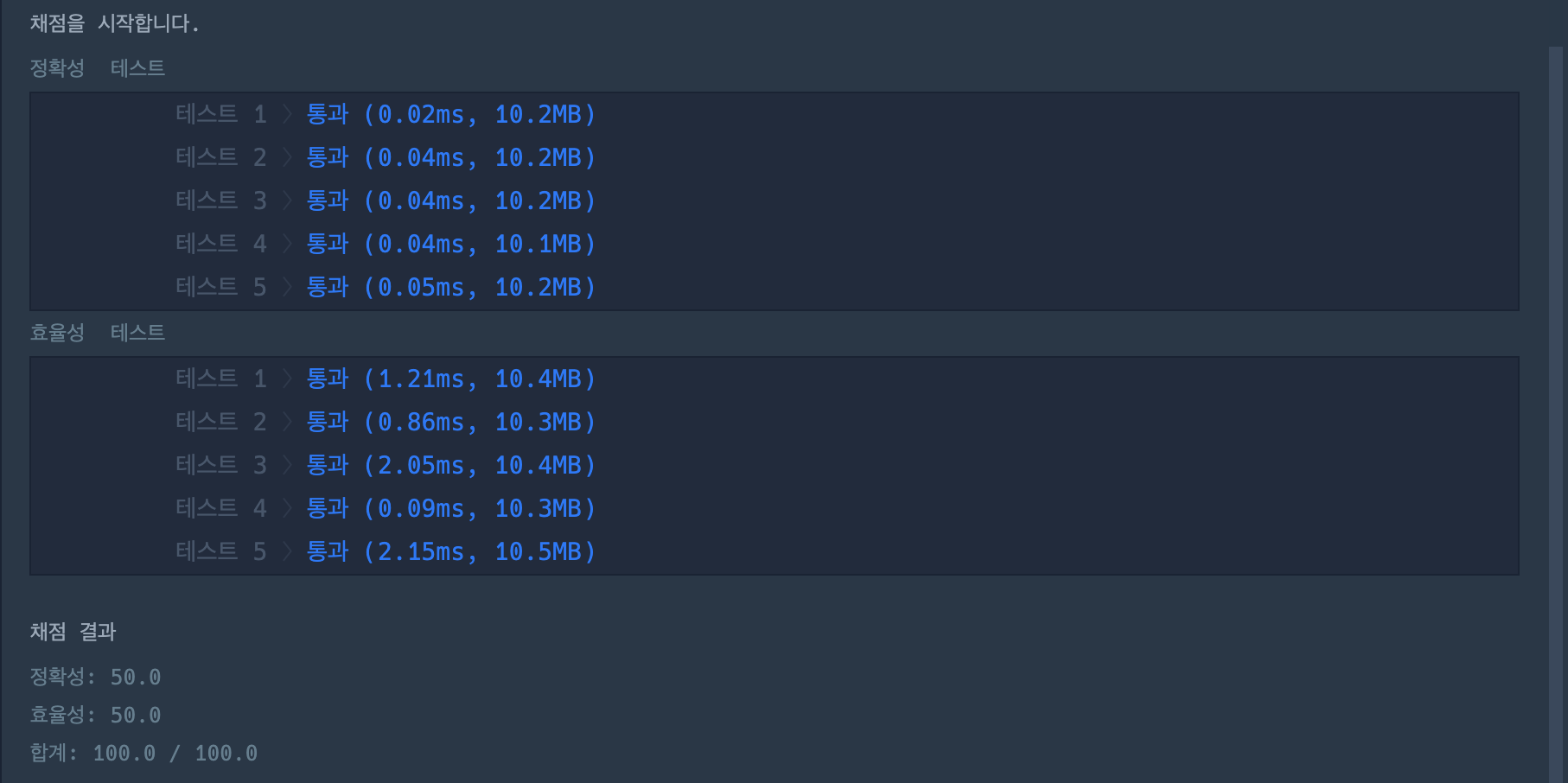
https://programmers.co.kr/learn/courses/30/lessons/42884

겹치는게 제일 많은 구간부터 카메라를 설치하면 되지 않을까 해서 dictionary로 구현하여 풀었지만 결과는 시간초과...

from collections import defaultdict

def check(check_dict):
    for v in check_dict.values():
        if len(v)!= 0:
            return False
    return True

def get_high_value_key(check_dict):
    res_idx = -1
    res_len = -1
    
    for i, v in check_dict.items():
        if len(v) > res_len:
            res_len = len(v)
            res_idx = i
    return res_idx

def renew(routes):
    check_dict = defaultdict(lambda: [])
    
    for i, search in enumerate(routes):
        for j in range(search[0],search[1] + 1):
            check_dict[j].append(i)
    return check_dict

def solution(routes):
    answer = 0
    check_dict = renew(routes)
            
    while not check(check_dict):
        check_dict = renew(routes)
        out_key = get_high_value_key(check_dict)
        temp_list = check_dict[out_key][:]
        for num in temp_list:
            for v in check_dict.values():
                if num in v:
                    v.remove(num)
        new_routes = []
        for i,v in enumerate(routes):
            if i not in temp_list:
                new_routes.append(v)
        routes = new_routes
        
        answer += 1
            
    return answer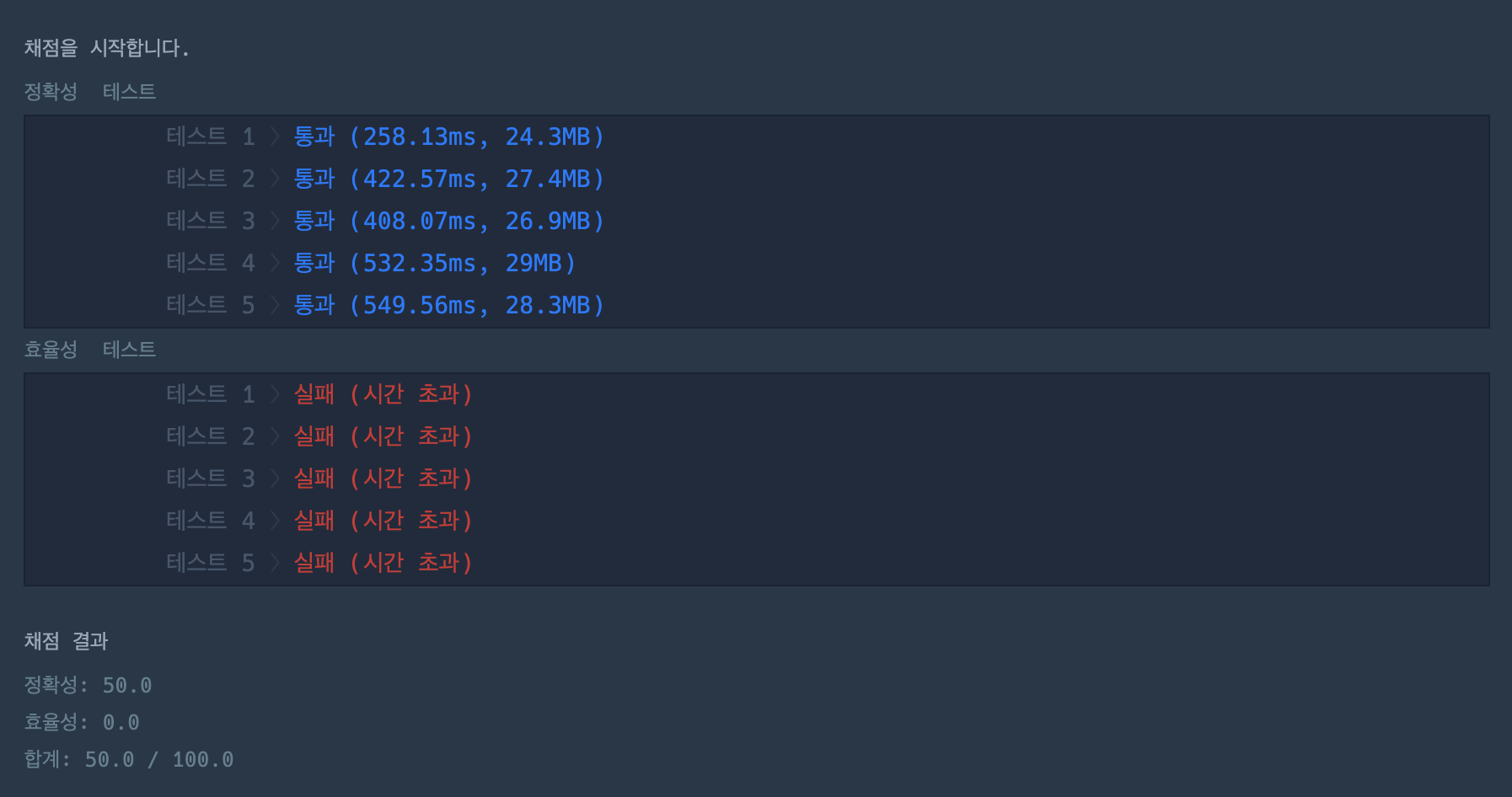

일단, 코드가 너무 복잡하고 데이터를 많이 저장해야 해서 예상은 했었다.
결국, 다른 풀이를 보았는데 탐욕법 문제를 좀 더 많이 풀어봐야 겠다.
https://ga0n.tistory.com/entry/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-%EB%8B%A8%EC%86%8D%EC%B9%B4%EB%A9%94%EB%9D%BC

진출순으로 오름차순 정렬 후 카메라 위치를 포함할 수 있을 때까지의 차량의 진출 시점의 최소값으로 갱신을 한 후 다음 차량의 진입 시점을 포함하지 못한다면 새로운 카메라를 설치하는 로직으로 구현했다

정렬과정도 있으니 대략 O(nlogn)으로 끝낼 수 있다.

def solution(routes):
    answer = 1 #초기 카메라 세팅
    
    routes.sort()
    
    camera = routes[0][1]
    
    for i in range(len(routes) -1):
        
        if camera > routes[i][1]: # 최대한 이전꺼의 차를 포함하는 진출 시점의 최소의 수를 구함
            camera = routes[i][1]
            
        if camera < routes[i+1][0]: # 다음 카메라를 포함하지 못하는 상황이라면 카메라 한대 더 설치
            answer += 1 
            camera = routes[i+1][1]
            
            
    return answer