Finding simialr items
큰 집합에서 유사한 item을 찾는 일반적인 방법은
각 모든 조합을 찾아서 비교하는 것인데 이는 가장 정확하지만 비효율적이다.
그렇다면 조금 더 빠른 방법은 없을까?
LSH(Locality Sensitive Hashing) 의 개념
이름부터 hsah의 일종임을 알려주고 있다.
hashing을 통해서 동일한 값을 찾을 수는 있었지만 유사한 값을 찾는 개념이 조금은 어색하다
LSH의 과정은 다음과 같다.
- 여러개의 해쉬함수를 사용해서 item들을 bucket에 넣는다.
- 이 과정에서 적어도 한 번 같은 bucket에 들어간 조합들을 찾는다.
- 위에서 찾은 조합들에 대해서 비교해본다.
같은 bucket에 들어간 조합들에 대해서만 검증이 이루어지므로, 비교하는 횟수가 크게 줄어든다.
하지만 false-negative(실제로는 similar items이지만 다른 bucket에 들어감)같은 단점도 존재한다.
모든 문서나 data에 대해서 LSH를 바로 적용하면 좋겠지만
몇가지 과정을 거쳐야 한다.
Three Essential Techniques for Similar docs
Shingling
Minhashing
LSH focus on pairs of signatures likely to be similar
Shingling(convert docs to sets)
-
shingles: 문서에서 k-shingle이란 sequence of k characters, k개의 문자의 나열이다.
i.e. k=2 , docs = abcab
Set of 2-shingles = {ab,bc,ca} (집합이기에 중복 x) -
유사도와 Shingles
- 유사한 문서는 같은 shingle들이 많다.
- k-shingles에서 단어를 바꾸면, 그 단어로부터 k-1거리내의 shingles만 영향을 받는다.
- 재배치의 경우 재배치된 경계에서 2k거리의 shingles만 영향을 받는다
-
적절한 k
- k가 작으면 특징을 추출하기 어렵다.
- if k=1 shingles = {a,b,c,...,z} => 유사한 shingle이 너무 많음
- 주로 8,9,10 정도의 k를 사용한다.
- k가 작으면 특징을 추출하기 어렵다.
- Tokens
- k=10, 영어의 경우 shingles = 26^10, 하지만 저장공간의 경우 10byte = 256^10
- 너무 많은 공간을 차지하기 때문에 4byte 정도로 hsah
- 문서를 k-shingles set으로 표현하고 이를 token set으로 hash
- 같은 shingles은 hash value가 같도록
Minhashing (convert large sets to short signatures (preserving similarity))
- jaccard similarity
- 두 집합의 교집합의 크기를 합집합의 크기로 나눈 것
- 교집합만 있었다면 크기가 큰 집합에게 유리하지만 합집합으로 나눠줌으로 보정이 들어가
나름 공정한 방법이라 할 수 있다.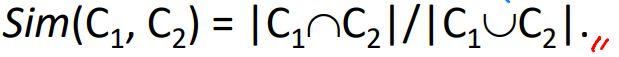
-
From Sets to Boolean Matrices
-
rows: 가능한 모든 원소의 집합 (U)
- k-shingles, token 의 집합
-
col: 집합 (문서)
-
(e,s)에서 e가 S의 포함되면 1 아니면 0
-
개념적인 행렬임

-
type of row
- a 1 1
- b 1 0
- c 0 1
- d 0 0
-
col 간의 유사도 (jaccard similarity와 동일)
- Sim(c1,c2) = a/(a+b+c)
-
-
Minhashing(개념적인 방법)
- 행을 뒤섞음(permute) .
- 이 뒤섞음 마다 minhash func h(c)적용
- h(c) = 행이 섞인상태에서 처음 1을 만나는 행 번호
- 모든 행에대해서 h(c)를 구함
- 행의 순서를 바꿀때마다 위의 과정을 거침
- 위의 결과를 가지고 signature matrix를 만듬
+ row : h(c)
+ col : c의 집합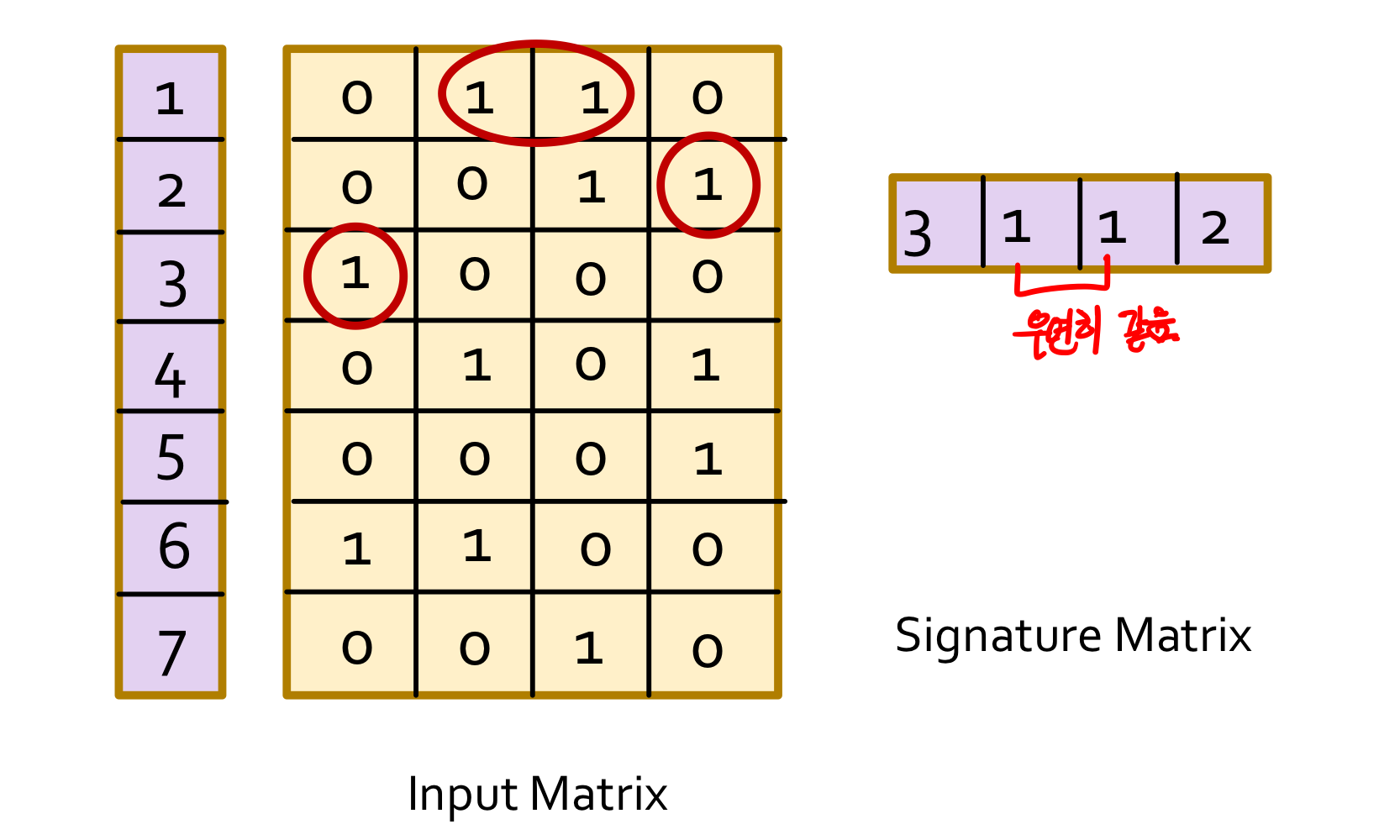
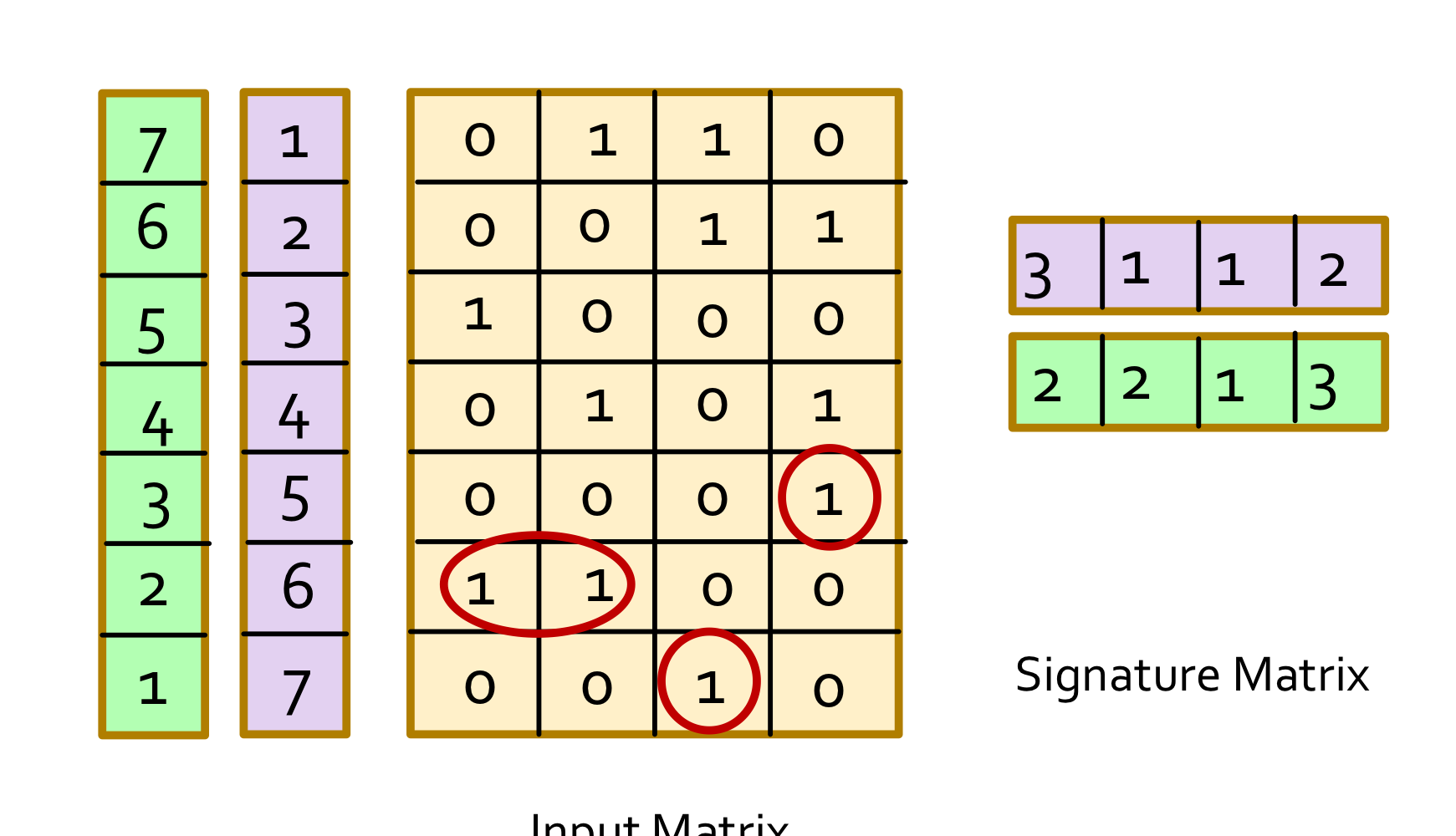
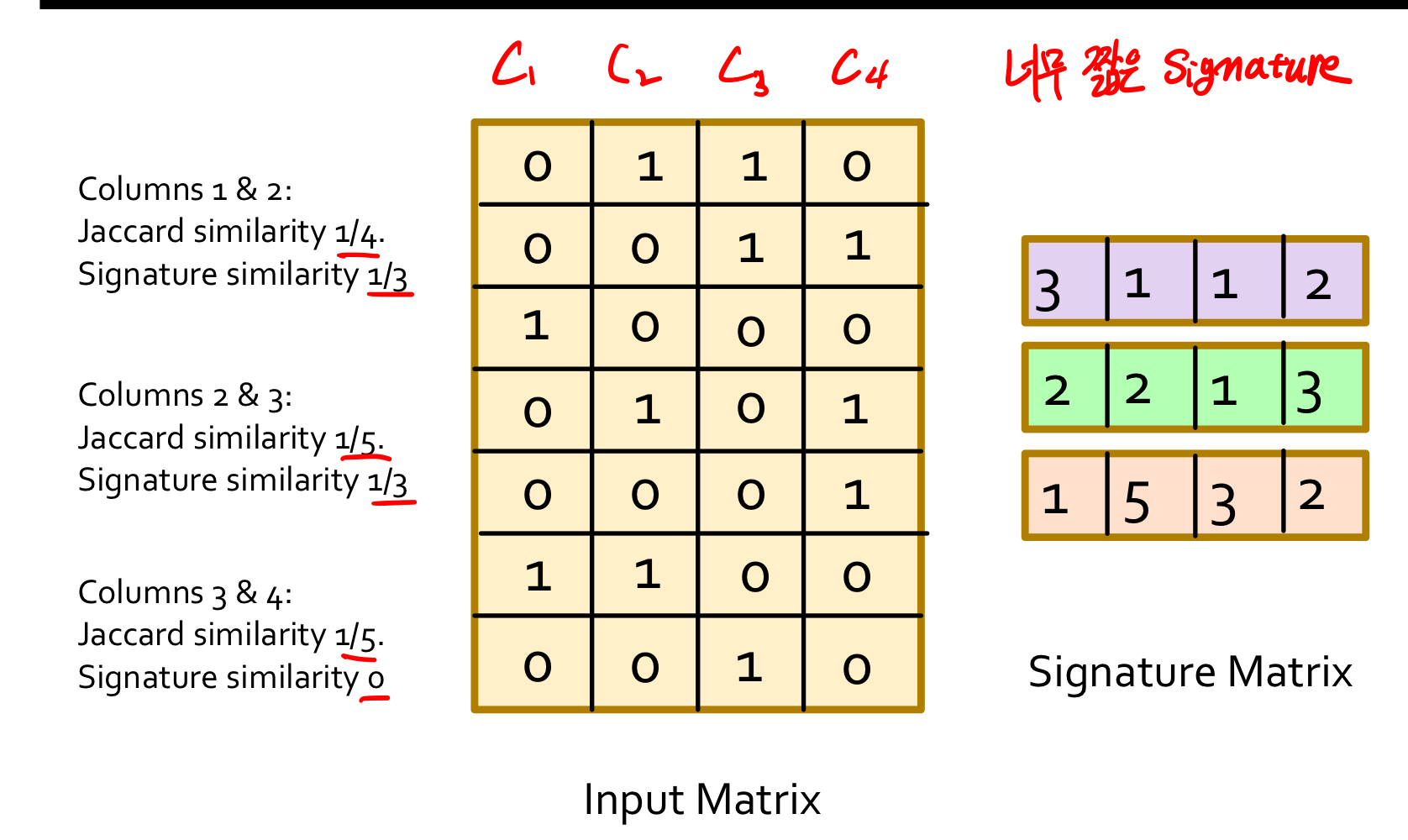
-
h(c1)=h(c2)일 확률은 Sim(c1,c2)와 동일하다
-
Sim(c1,c2) = a/(a+b+c)
-
h(c1) = h(c2)인 경우는 type-a row일 경우이고 나머지는 b,c의 경우
-
따라서 위 2가지는 확률적으로 동일하다.
-
충분한 길이의 signatures는 hashing후에도 유사도를 보존 다시말해 signature가 너무 짧으면 유사도를 보존하기 힘든 경우가 있다는 이야기
(이미지 교체 예정)
-
-
Minhashinig의 실제 구현
-
permutation을 많은 hash function으로 근사
- 당연히 겹치는 경우가 생길 수 있음
-
위에서 사용한 hash value가 새로 바뀐 행의 번호
-
각 Column c에 대해서 hash func hi는 M(i,c)를 가진다.
-
각 row r, colummn c에 대해서 r에서 c가 1일 때 , hi(c)의 가장 작은 값이 M(i,c)가 된다.
(이미지 교체 예정) -
c 에대해서 1인 row가 바뀐 행 번호를 보고 가장 적은 걸 찾는 과정
-
실제 permutation하고 찾는것과 유사.
-
-
조금 더 향상된 Minhashing
- minhashing 의 cost는 row의 크기에 비례
- 그렇다면 처음 1000개의 row만 hashing 한다면?
- 시간을 크게 절약할 수 있지만 처음 1000열이 전부 0이라면 hash값을 얻을 수 없다. (애초에 비슷한 문서가 아니었을 가능성이 크다)
- row를 k개의 band로 나누고 각 밴드마다 새로운 해쉬함수를 적용
- 적절한 K를 설정하는데 주의가 필요하다
- minhashing 의 cost는 row의 크기에 비례

