LSH-3 (LSH Families)

Distance Measures

일반화된 LSH는 점 사이의 "거리"에 기반합니다 (비슷한 점은 가깝다)

• d => distance measure는 다음의 조건을 만족해야합니다

  1. d(x,y) >=0
  2. d(x,y) = 0 iff x=y
  3. d(x,y) = d(y,x)
  4. d(x,y) <= d(x,z) + d(z,y) (triangle inequality)

• 유클리드 거리

  • L2 norm: 우리가 흔히 쓰는 거리
  • L1 norm: 각 차원에서 차이의 합
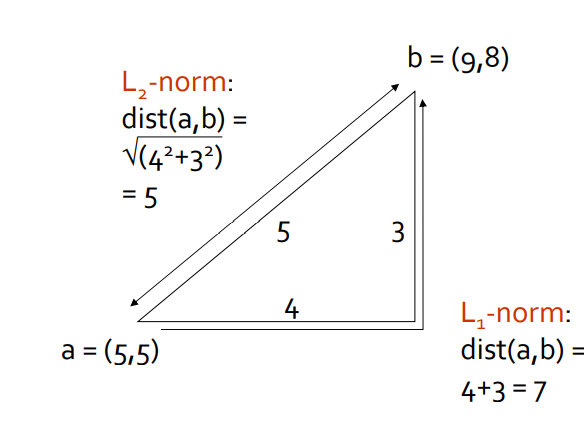
    • ex Maahattan disatnce
      

• 비유클리드 거리

  • jaccard distance = 1- jaccard similarity
  • cosine distance = angle between the vectors
    $d = \frac{p1 \cdot p2}{\vert p1\vert\vert p2\vert}$
  • edit distance = 2개의 문자열을 동일하게 만드는데 몇번의 삽입삭제가 필요한가
    $d = \vert x\vert + \vert y\vert -2\vert LCS(x,y)\vert\\ LCS:\space Longest \space common \space susbsequence \space$

LSH Families of Hash Function

• 정의

  H hash 함수의 family 는 $(d_1,d_2,p_1,p_2)-sensitive$로 나타낼 수 있다.
  이것의 의미는 집합$S$에서 모든 $x,y$에 대해서 다음을 의미한다.

  1. if $d(x,y) \le d_1$ 이면 $H$의 원소 $h$에 대해 $h(x)=h(y)$일 확률이 적어도 $p_1$이다.
  2. if $d(x,y) \ge d_2$ 이면 $H$의 원소 $h$에 대해 $h(x)=h(y)$일 확률이 많으면 $p_2$이다.
     

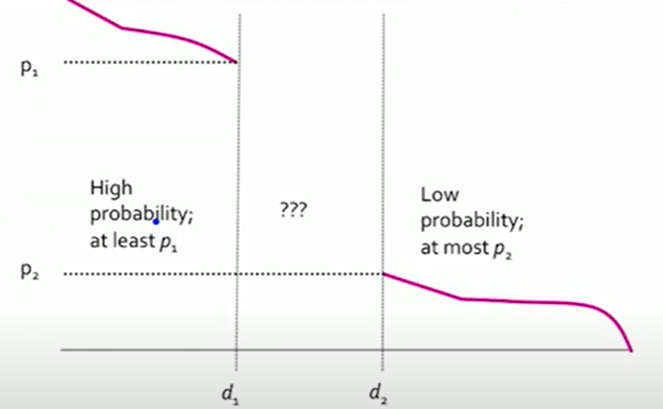
• Example

  • $S$: subsets of some universal set, $d$: jaccard distance, $H$: minhash 함수의 집합
    [$h(x) = h(y)$] = $sim(x,y)$ = $1 - d(x,y)$
  • H is a $(\frac{1}{3},\frac{3}{4},\frac{2}{3},\frac{1}{4})$- sensitive family for S and d
    *LSH faimly in consine distance : [$h(x) = h(y)$] = $1 - d(x,y)/180$

• LSH Family의 증폭

  • S-curve 함수의 효과를 위해
  • And (rows in band): $H' \space is \space (d_1,d_2,p_1^r,p_2^r)-sensitive$ (확률을 내리기때문에 d가 적은 구간에서 좋지 않음)
  • Or (many band):$H' \space is \space (d_1,d_2,1-(1-p_1)^b,1-(1-p_2)^b)-sensitive$(확률을 올리기 때문에 d가 큰 구간에서 좋지 않음)
  • And - Or: $H' \space is \space (d_1,d_2,1-(1-p_1^r)^b,1-(1-p_2^r)^b)-sensitive$
  • Or-And: $H' \space is \space (d_1,d_2,(1-(1-p_1)^b)^r,(1-(1-p_2)^b))^r-sensitive$
  • 역시 적절한 b,r을 통해 적당한 threshold t를 찾아야한다.