그래프

창고지기·2025년 7월 14일

알고리즘

알고리즘스터디

목록 보기

23/60

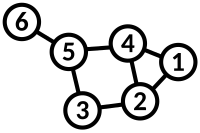
1.그래프란?

정점(Vertex)과 간선(edge)로 구성된 비선형 자료구조.

출처

2. 주요 용어

정점 : 그래프의 기본 구성요소
간선 : 정점과 정점을 연결하는 선
방향/무방향 : 간선의 방향이 있다면 그 방향으로만 이동 가능. 방향이 없다면 양 방향으로 이동 간,ㅇ
가중치 : 간선에 값을 부여할 수 있음. (거리, 비용 등)
연결 : 그래프의 모든 노드들 사이의 경로가 존재하면 연결 그래프
차수 : 무방향에서는 인접한 노드의 수, 방향에서는 진입 차수와 진출 차수로 나눔.
Cycle : 한 노드에서 시작에서 자기 자신으로 돌아오는 경로가 있는경우 이 경로를 Cycle이라 부른다.

3. 그래프의 구현

1) 인접 행렬 (Adjacency Matrix)

그래프를 2차원 배열을 사용해서 표현한다.
matrix[from][to] = weight(or bool)
- from에서 to로 가는 경로의 가중치는 weight이다 (혹은 경로가 존재한다.)
- 대각선의 경우(from = to)를 잘 처리할 것.
- 무방향 그래프인 경우 반대의 경우도 추가.
메모리를 많이 차지한다. 정점은 많지만 간선이 적은 경우 낭비.
탐색에 유리하다 $O(1)$

2) 인접 리스트 (Adjacency List)

그래프를 리스트를 사용해서 표현
List[from].push_back(to)
- from에의 인접노드를 리스트로 관리
- 가중치는 map, pair등 다양한 방법으로 추가 가능
- 무방향 그래프인 경우 반대의 경우도 추가.
메모리를 적게 먹지만, 탐색은 $O(N)$ .

3) 발생 행렬 (Incidence matrix)

2차원 배열을 이용해서 표현하지만 조금 독특하다.
행은 정점 리스트, 열은 간선 리스트
- 열을 순회하면서 간선과 연결된 정점은 1 아니면 0
- 방향 그래프인 경우 들어가면 1 나가면 -1
  
  e1 e2 e3 e4
  1 1 1 1 0
  2 1 0 0 0
  3 0 1 0 1
  4 0 0 1 1
  
  출처

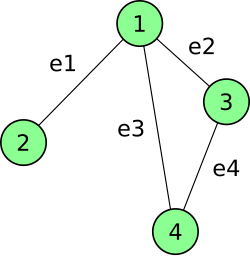
	e1	e2	e3	e4
1	1	1	1	0
2	1	0	0	0
3	0	1	0	1
4	0	0	1	1

4. 그래프 탐색

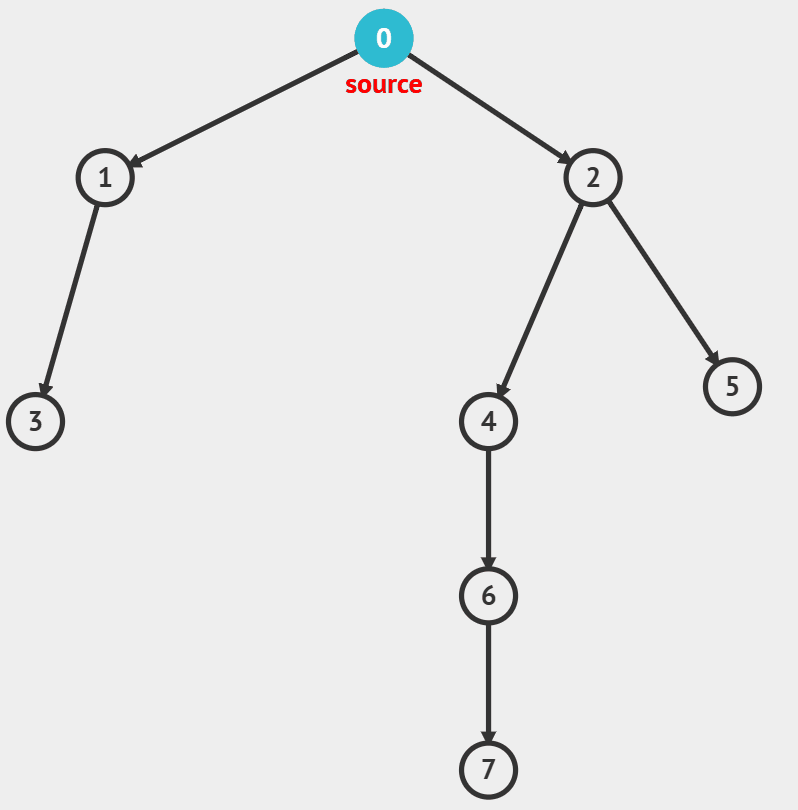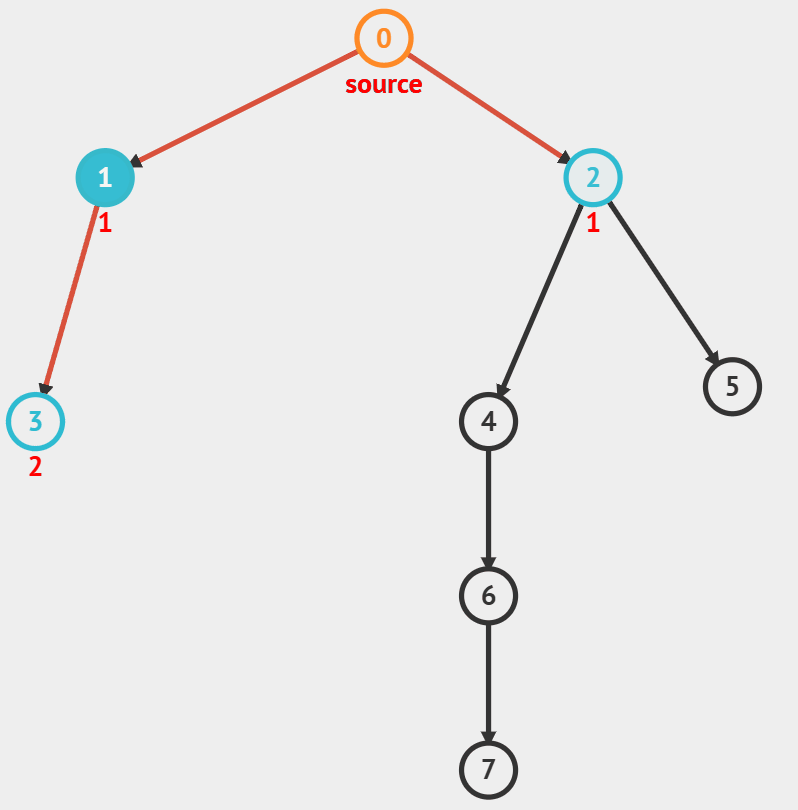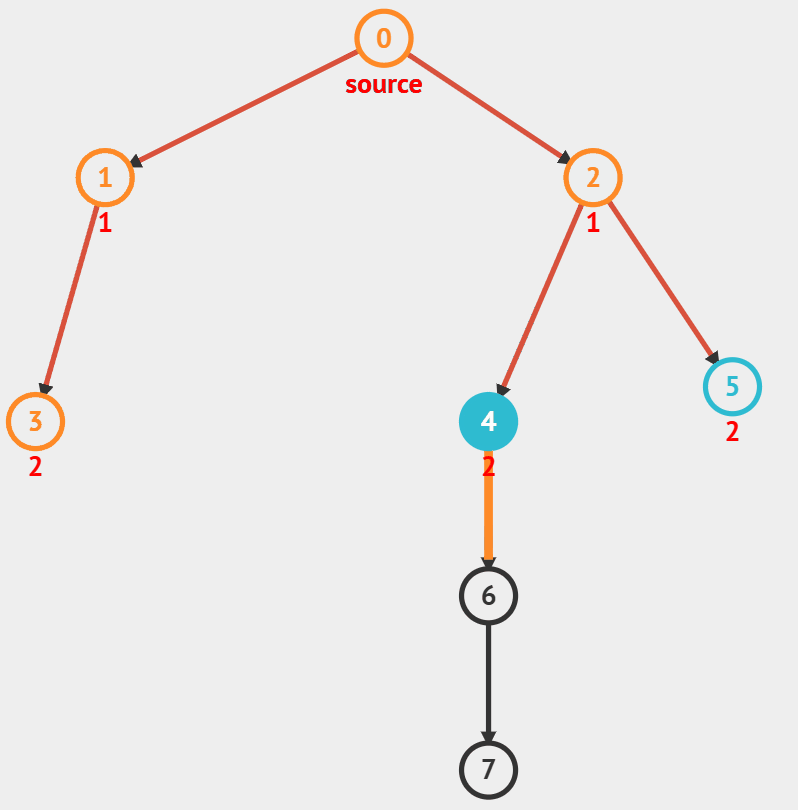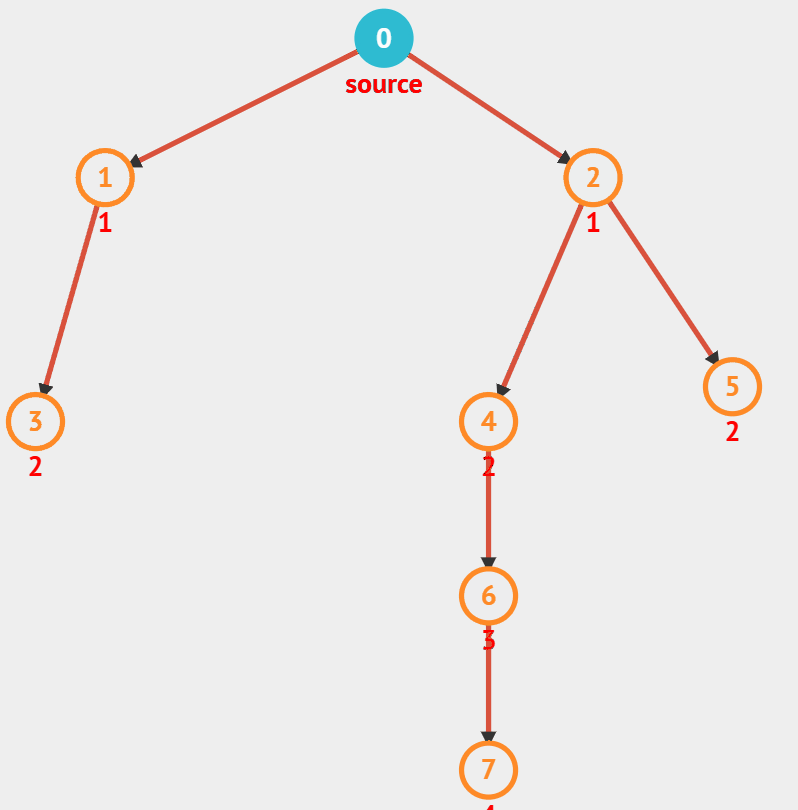
1) DFS

깊이 우선 탐색(Depth First Search), 말 그대로 갈 수 있는 최대 깊이까지 탐색하는 걸 우선으로 한다.
재귀 혹은 스택을 활용해서 구현한다.
모든 경로 방문, 특정 노드 사이의 경로 있는지 확인, 사이클이 있는지 확인
stack이 빌 때까지 다음을 반복
- top을 가져온 후 pop
- top 정점의 방문여부를 확인
  - 방문 하지 않은 경우
    - 방문처리 후 top의 인접노드삽입 (삽입 순서는 조건에 따라서 ,오름차순으로 방문 원하면 큰거부터 넣어야)
  - 방문 한 경우
    - 아무것도 안함.

출처 : visualgo.net

재귀를 통한 DFS 구현

#include <iterator>
#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

unordered_map<int, vector<int>> adjList;
vector<char> result;
vector<bool> visited;

void DFS(int start)
{
    if (visited[start]) return;
    result.push_back(start + 'A');
    visited[start] = true;
    for (auto& adjNode : adjList[start])
    {
        DFS(adjNode);
    }
}

vector<char> solution(vector<pair<char, char>> graph, char start)
{
    visited.resize(26,false);
    result = vector<char>(0);

    for (auto& [from, to] : graph)
    {
        adjList[from-'A'].push_back(to-'A');
    }

    DFS(start-'A');

    return result;
}

void init()
{
  adjList.clear();
  result.clear();
  visited.clear();
}

void print(vector<char> vec)
{
  copy(vec.begin(), vec.end(), std::ostream_iterator<char>(cout, " "));
  cout << endl;  
}

int main()
{
  //bool 반환할 때 true는 1, false는 0 입니다.
  print(solution({{'A', 'B'}, {'B', 'C'}, {'C', 'D'}, {'D', 'E'}}, 'A')); //출력값 : A B C D E
  init();
  print(solution({{'A', 'B'}, {'A', 'C'}, {'B', 'D'}, {'B', 'E'}, {'C', 'F'}, {'E', 'F'}}, 'A')); //출력값 : A B D E F C

  return 0;
}

2) BFS

너비 우선 탐색(Breadth First Search) 시작 노드에서 제일 가까운 노드들을 먼저 탐색한다.
큐를 활용해서 구현한다.
최단 경로
queue가 빌 때까지 다음을 반복
- front를 가져온 후 pop
- front의 인접 노드들 중 방문하지 않은 노드가 있으면 방문 처리하고 삽입.(삽입 순서는 조건에 따라서)

출처 : visualgo.net

BFS 구현

  //아래 코드는 테스트 코드 입니다.
#include <iterator>
#include <iostream>
#include <vector>
#include <unordered_map>
#include <unordered_set>
#include <queue>

using namespace std;

unordered_map<int, vector<int>> adjList;
vector<int> result;
unordered_set<int> visited;

void BFS(int start)
{
    queue<int> q;
    q.push(start);
    visited.insert(start);
    result.push_back(start);

    while(!q.empty())
    {
        int front  = q.front();
        q.pop();
        for (auto& adj : adjList[front])
        {
            if (visited.find(adj) == visited.end())
            {
                visited.insert(adj);
                result.push_back(adj);
                q.push(adj);
            }
        }
    }
}

vector<int> solution(vector<pair<int,int>> graph, int start)
{
    for (auto& [from, to] : graph)
    {
        adjList[from].push_back(to);
    }

    BFS(start);

    return result;
}

void init()
{
  adjList.clear();
  result.clear();
  visited.clear();
}

void print(vector<int> vec)
{
  copy(vec.begin(), vec.end(), std::ostream_iterator<int>(cout, " "));
  cout << endl;
}

int main()
{

  print(solution({{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 6}, {3, 7}, {4, 8}, {5, 8}, {6, 9}, {7, 9}}, 1)); //출력값 : 1 2 3 4 5 6 7 8 9
  init();
  print(solution({{0, 1}, {1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 0}}, 1)); //출력값 : 1 2 3 4 5 0

  return 0;
}

DFS와 BFS의 visited 처리 순서에 주의

DFS는 다음에 방문할 노드를 삽입
BFS는 지금 방문할 노드를 삽입

5. 최단 경로

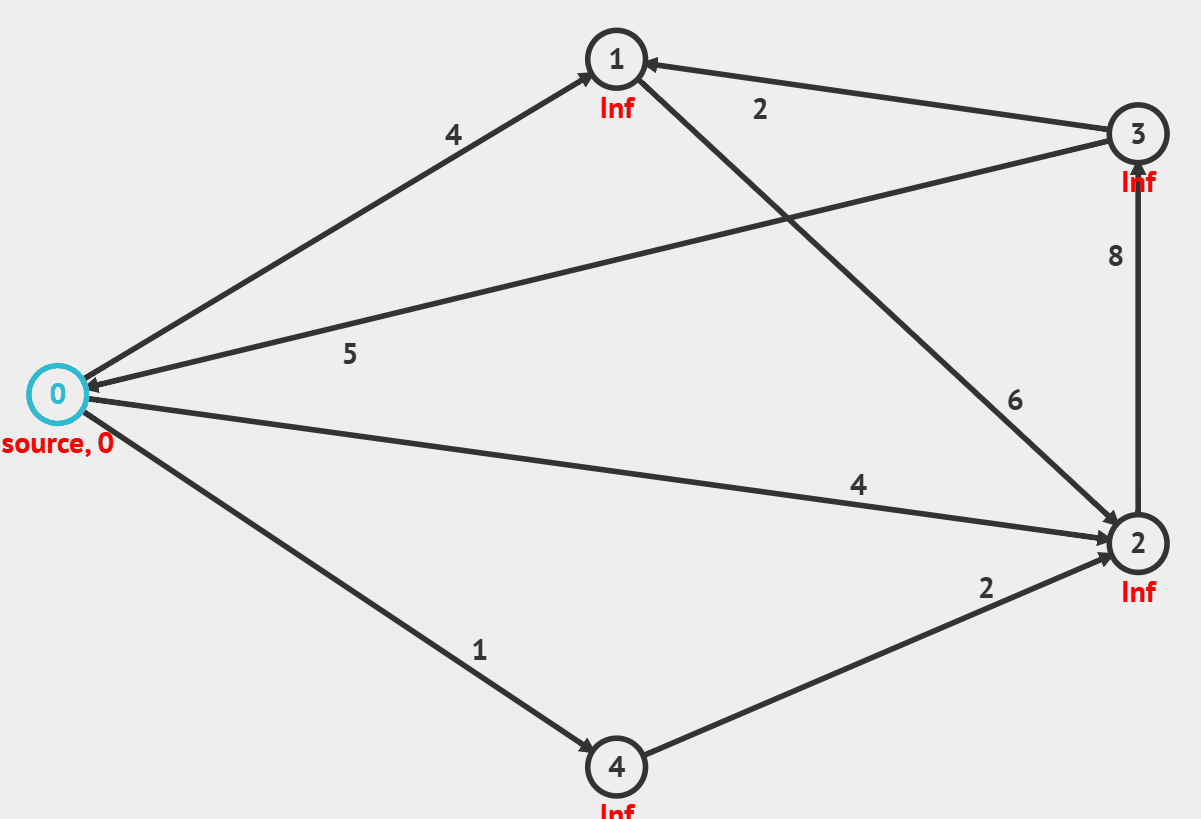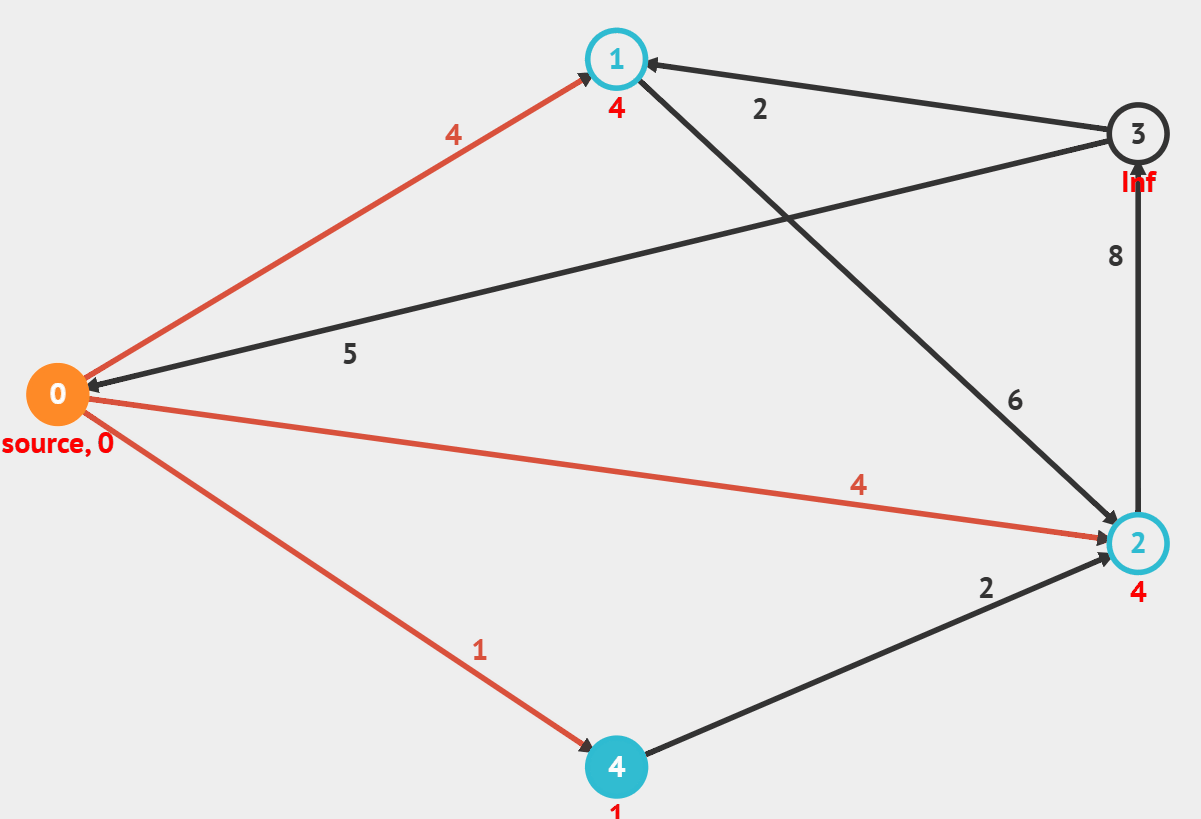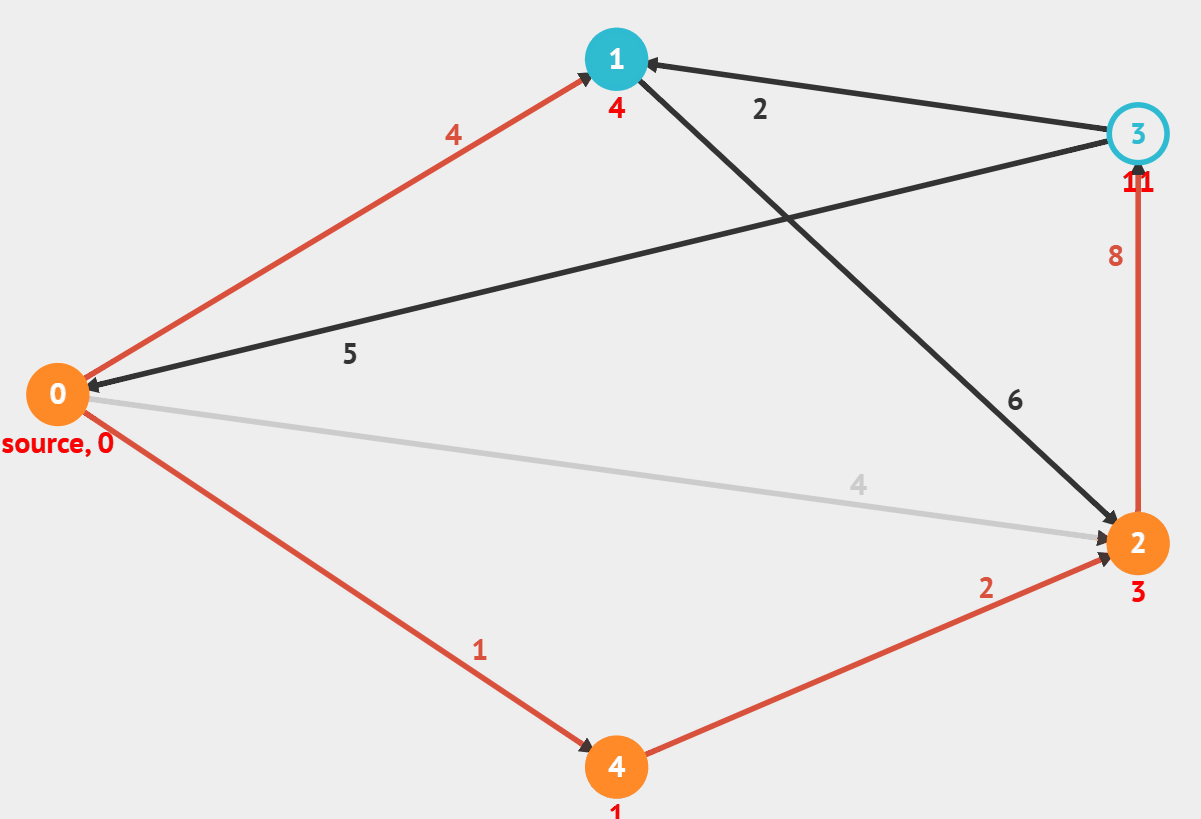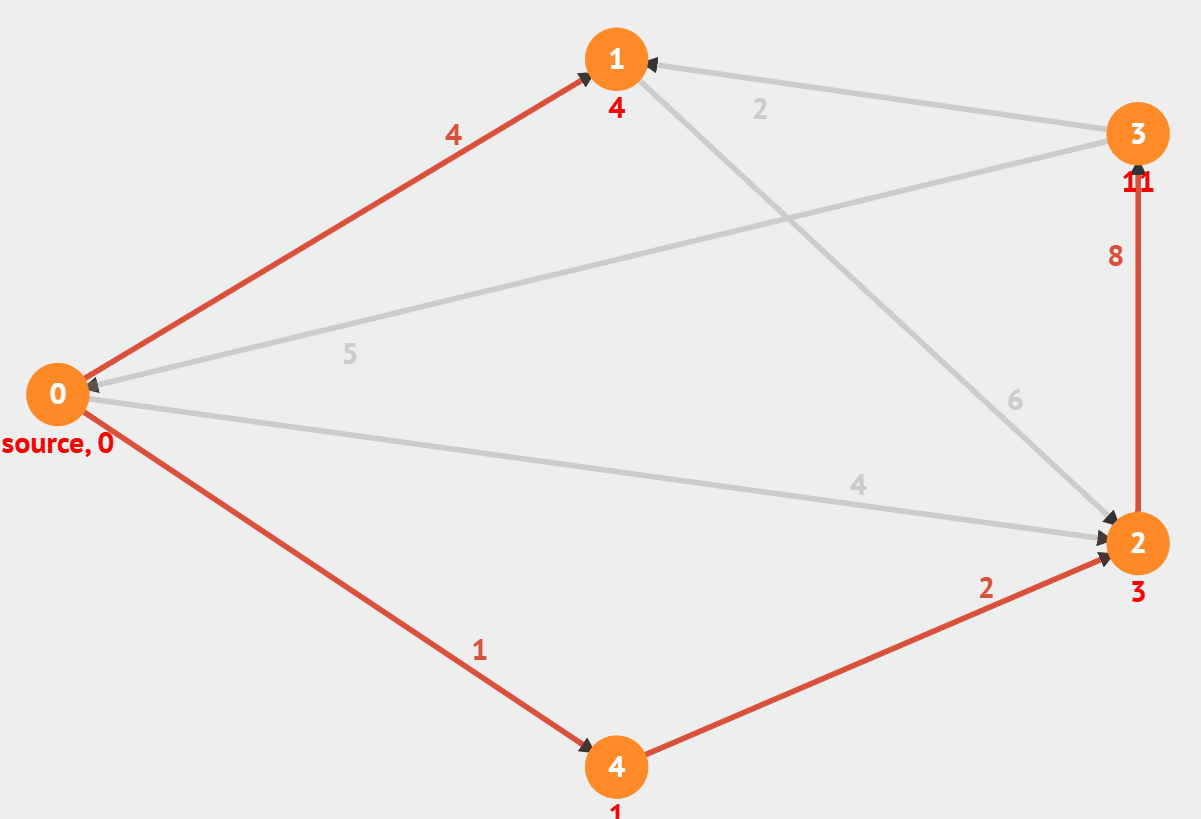
1) 다익스트라 (Dijkstra)

시작 노드에서 다른 모든 노드에 도달하는 최단 경로를 구하는 알고리즘
음의 가중치가 있는 경우 사용 불가
시작 노드 설정 ( 최소 비용 = 0, 직전 노드는 자기 자신)
나머지 노드들의 최소비용은 INF, 직전 노드 또한 INF
그래프에서 방문할 수 있는 노드중 현재까지의 최소 비용이 가장 작은 노드 선택.
- 해당 노드를 거쳐서 인접 노드에 가는 것과 기존의 경로 중 작은 값으로 갱신 (직전 노드도 갱신)

출처 : visualgo.net

#include <iterator>
#include <iostream>
#include <vector>
#include <unordered_map>
#include <queue>
#include <climits>

using namespace std;

unordered_map<int, vector<pair<int, int>>> graph;
vector<vector<int>> dijkstraVec;

void Dijkstra(int start, int numNodes)
{
    dijkstraVec.clear();
    //[0] 시작점에서 i까지의 거리
    //[1] i의 직전 노드
    dijkstraVec.resize(numNodes, vector<int>(2, INT_MAX));
    //최소비용
    dijkstraVec[start][0] = 0;
    //직전 노드
    dijkstraVec[start][1] = 0;
    vector<bool> visited(numNodes,false);
    auto cmp = [](const pair<int,int>& a, const pair<int,int>& b){
        return a.first > b.first;
    };
    // dist, 노드번호
    priority_queue<pair<int,int>, vector<pair<int,int>>, decltype(cmp)> unVisited(cmp);
    unVisited.push({0, start});

    // 거리 정보가 갱신된 노드만 q에 넣음
    // 연결 그래프라면 모든 노드를 탐방
    while(!unVisited.empty())
    {
        auto& [dist, u] = unVisited.top(); unVisited.pop();
        if (visited[u]) continue;
        visited[u] = true;

        for (auto& [v, weight] : graph[u])
        {
            if (visited[v]) continue;
            if (dijkstraVec[v][0] > dist + weight)
            {
                dijkstraVec[v][0] = dist + weight;
                dijkstraVec[v][1] = u;
                unVisited.push({dijkstraVec[v][0], v});
            }
        }
    }
}

vector<int> solution(int start, int numNodes, vector<tuple<int, int, int>> edges)
{
    vector<int> answer;
    graph.clear();

    for (auto& [from, to, weight] : edges)
    {
        graph[from].push_back({to, weight});
    }

    Dijkstra(start, numNodes);
    for (auto& v : dijkstraVec)
    {
        answer.push_back(v[0]);
    }

    return answer;
}

void print(vector<int> vec)
{
  copy(vec.begin(), vec.end(), std::ostream_iterator<int>(cout, " "));
  cout << endl;
}

int main()
{  
  print(solution(0, 3, {{0, 1, 9},{0, 2, 3},{1, 0, 5},{2, 1, 1}})); //출력값 : 0 4 3
  print(solution(0, 4, {{0, 1, 1}, {1, 2, 5}, {2, 3, 1}})); //출력값 : 0 1 6 7

  return 0;
}

2) 벨만 포드 (Bellman - Ford)

시작 노드에서 다른 모든 노드에 도달하는 최단 경로를 구하는 알고리즘
다익스트라와 달리 매 단계마다 모든 간선의 최소비용 갱신
음의 사이클이 있는 경우 사용 불가.
시작 노드 설정 ( 최소 비용 = 0, 직전 노드는 자기 자신)
나머지 노드들의 최소비용은 INF, 직전 노드 또한 INF

다음을 노드개수 -1 만큼 반복
시작 노드 u에서 임의의 노드k를 거쳐서 다른 노드 v로 가는 경로 u->k->v 가 u->v보다 값이 작으면 정보 갱신
마지막으로 위의 과정을 한번 더 시행
- 만약 최소 값이 갱신되면 음의 사이클이 존재.
- 최소경로 보장 x

출처 : visualgo.net

#include <iterator>
#include <iostream>
#include <vector>
#include <unordered_map>
#include <unordered_set>
#include <climits>
#include <algorithm>

using namespace std;
unordered_set<int> allvertices;
unordered_map<int, vector<pair<int,int>>> graph;
// <minVAl,u> 
unordered_map<int, pair<int,int>> distAndUList;
bool BellmanFord(int source)
{
    for(auto& vertex : allvertices)
    {
        distAndUList[vertex] = make_pair(INT_MAX, INT_MAX);
    }
    distAndUList[source] = {0,0};

    for (int i=0; i<allvertices.size()-1; i++)
    {
        // k = 거쳐갈 노드
        for (auto& k : allvertices)
        {
            if (distAndUList[k].first == INT_MAX) continue;
            //u->k->v 와 비교해서 값 갱신
            for (auto& [v, weight] : graph[k])
            {
                if (distAndUList[v].first > distAndUList[k].first + weight)
                {
                    distAndUList[v].first = distAndUList[k].first + weight;
                    distAndUList[v].second = k;
                }
            }
        }
    }

    // k = 거쳐갈 노드
    for (auto& k : allvertices)
    {
        //u->k->v 와 비교해서 값 갱신
        for (auto& [v, weight] : graph[k])
        {
            if (distAndUList[k].first == INT_MAX) continue;
            //u->k->v 와 비교해서 값 갱신

            if (distAndUList[v].first > distAndUList[k].first + weight)
            {
                return false;
            }
        }
    }
    return true;
}

vector<int> solution(int num_vertices, vector<tuple<int, int, int>> edges, int source)
{
    vector<int> answer;

    // 간선을 정보를 통해서 그래프의 구조 파악
    for(auto& [from, to, weight] : edges)
    {
        allvertices.insert(from);
        allvertices.insert(to);
        graph[from].push_back({to, weight});
    }

    bool belowZeroCycle = !BellmanFord(source);
    vector<pair<int, int>> sortedDist;
    for (auto& [v, data] : distAndUList) 
    {
        sortedDist.push_back({v, data.first}); // v: 정점 번호, data.first: 거리
    }

    sort(sortedDist.begin(), sortedDist.end()); // v 기준 정렬

    if (!belowZeroCycle)
    {
        for (auto& [u , dist] : sortedDist)
        {
            answer.push_back(dist);
        }
    }
    else
    {
        answer.push_back(-1);
    }

    return answer;
}

void print(vector<int> vec)
{
  copy(vec.begin(), vec.end(), std::ostream_iterator<int>(cout, " "));
  cout << endl;
}

int main()
{
  print(solution(5, {{0, 1, 4}, {0, 2, 3}, {0, 4, -6}, {1, 3, 5}, {2, 1, 2}, {3, 0, 7}, {3, 2, 4},{4, 2, 2}}, 0)); //출력값 : 0 -2 -4 3 -6
  print(solution(4, {{0, 1, 5}, {0, 2, -1}, {1, 2, 2}, {2, 3,-2}, {3, 0, 2}, {3, 1, 6}}, 0)); //출력값 : -1

  return 0;
}

3) 플로이드 워셜 (Floyd-Warshall)

위의 2가지 방법은 시작 노드를 설정하고 최단 거리를 찾는다.
플로이드 워셜은 모든 노드간의 최소 경로를 구해준다.
$D_{ab} = min(D_{ab}, D_{ak} + D_{kb})$

//아래 코드는 테스트 코드 입니다.
#include <iterator>
#include <iostream>
#include <vector>
#include <unordered_map>
#include <unordered_set>
#include <climits>
#include <algorithm>

using namespace std;
unordered_set<int> allvertices;
unordered_map<int, vector<pair<int,int>>> graph;
vector<vector<int>> distanceMatrix;
int n = 0;

void FW()
{
    distanceMatrix.resize(n, vector<int>(n,INT_MAX));
    for (int i=0; i<n; i++)
    {
        distanceMatrix[i][i] = 0;
    }

    for(auto& [from, data] : graph)
    {
        for (auto& [to, weight] : data)
        {
            distanceMatrix[from][to] = weight;
        }
    }

    for (int k = 0; k < n; k++)
    {
        for (int i = 0; i < n; i++)
        {
            for (int j=0; j < n; j++)
            {
                if (distanceMatrix[i][k] != INT_MAX && distanceMatrix[k][j] != INT_MAX)
                {
                    distanceMatrix[i][j] = min(distanceMatrix[i][j], distanceMatrix[i][k] + distanceMatrix[k][j]);
                }
            }
        }
    }
}

vector<int> solution(vector<tuple<int, int, int>> edges)
{
    graph.clear();
    allvertices.clear();
    distanceMatrix.clear();
    n = 0;
    vector<int> answer;

    // 간선을 정보를 통해서 그래프의 구조 파악
    for(auto& [from, to, weight] : edges)
    {
        if(allvertices.insert(from).second) n++;
        if(allvertices.insert(to).second) n++;
        graph[from].push_back({to, weight});
    }

    FW();


    for (int i = 0; i < n; i++) 
    {
        // 음수 사이클 존재
        if (distanceMatrix[i][i] < 0)
        {
            answer.push_back(-1);
            return answer;
        }
    }

    vector<int> temp(allvertices.begin(), allvertices.end());
    sort(temp.begin(), temp.end());

    // 값을 확인하기 위한 출력코드
    int source = 0;
    for (int v : temp)
    {
        answer.push_back(distanceMatrix[source][v] == INT_MAX ? -1 : distanceMatrix[source][v]);
    }

    return answer;
}

void print(vector<int> vec)
{
  copy(vec.begin(), vec.end(), std::ostream_iterator<int>(cout, " "));
  cout << endl;
}

int main()
{
  print(solution({{0, 1, 4}, {0, 2, 3}, {0, 4, -6}, {1, 3, 5}, {2, 1, 2}, {3, 0, 7}, {3, 2, 4},{4, 2, 2}})); //출력값 : 0 -2 -4 3 -6
  print(solution({{0, 1, 5}, {0, 2, -1}, {1, 2, 2}, {2, 3,-2}, {3, 0, 2}, {3, 1, 6}})); //출력값 : -1

  return 0;
}