모듈러 역원

관용 암호화 또는 공개키 암호화 등에서 곱셈에 대한 모듈러 역원을 필요로하는 경우가 더러 있습니다.
이는 유클리드 알고리즘을 통해 조금 더 쉽게 구할 수 있습니다.

유클리드 알고리즘

$gcd(a,b)=gcd(b,r)$ $r=a\space mod\space b$


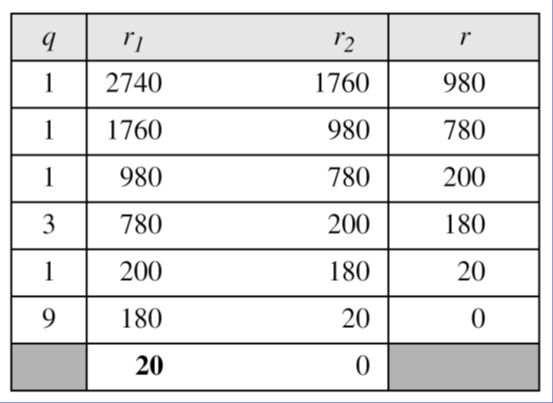
$q:$몫, $r:r1$을 $r2$로 나눈 나머지 ($r=r1-q*r2)$

확장 유클리드 알고리즘

$s\times a + t\times b =gcd(a,b)$


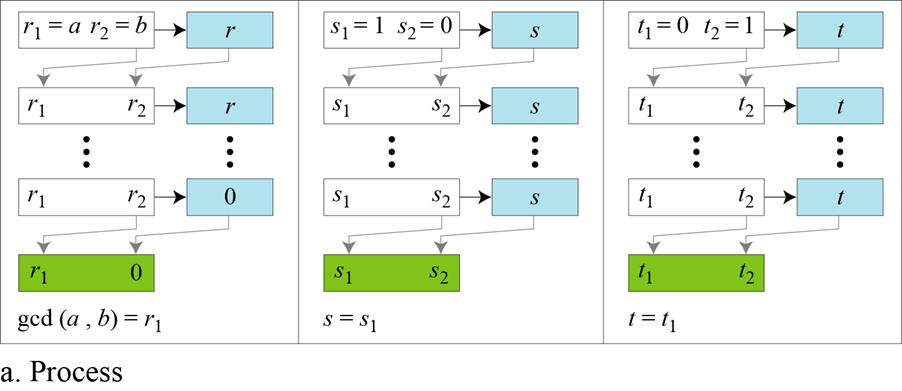
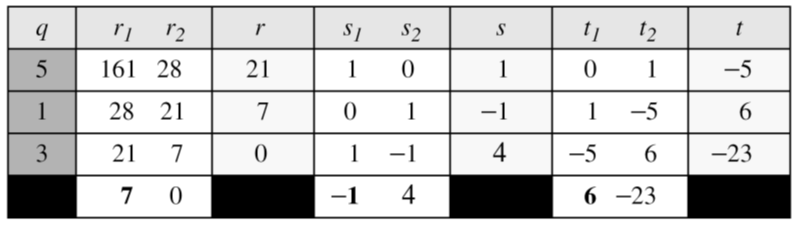
위와 동일한 방법으로 단계를 진행하지만 $s_1=1,s_2=0,t_1=0,t_2=1$의 초기값을 가지고 $s$와$t$에 관해서도 진행

확장 유클리드 알고리즘을 통한 모듈러 역원

$s\times n+t\times b=gcd(n,b)$
$gcd(n,b)=1$이면 b는 $mod\space n$상에서 곱셈에 대한 역원을 가진다.

(1) $s\times n+t\times b=1 \space mod\space n$
(2) $0 + t \times b=1 \space mod\space n$ ($s\times n\space mod \space n =0$)
(3) $t \times b=1 \space mod\space n$
따라서 t는 b의 곱셈에 대한 역원이고 이 값은 확장 유클리드 알고리즘을 통해 도출해 낼 수 있다.