알고리즘 스터디 22일차

1. 양과 늑대

1) 문제

문제 설명
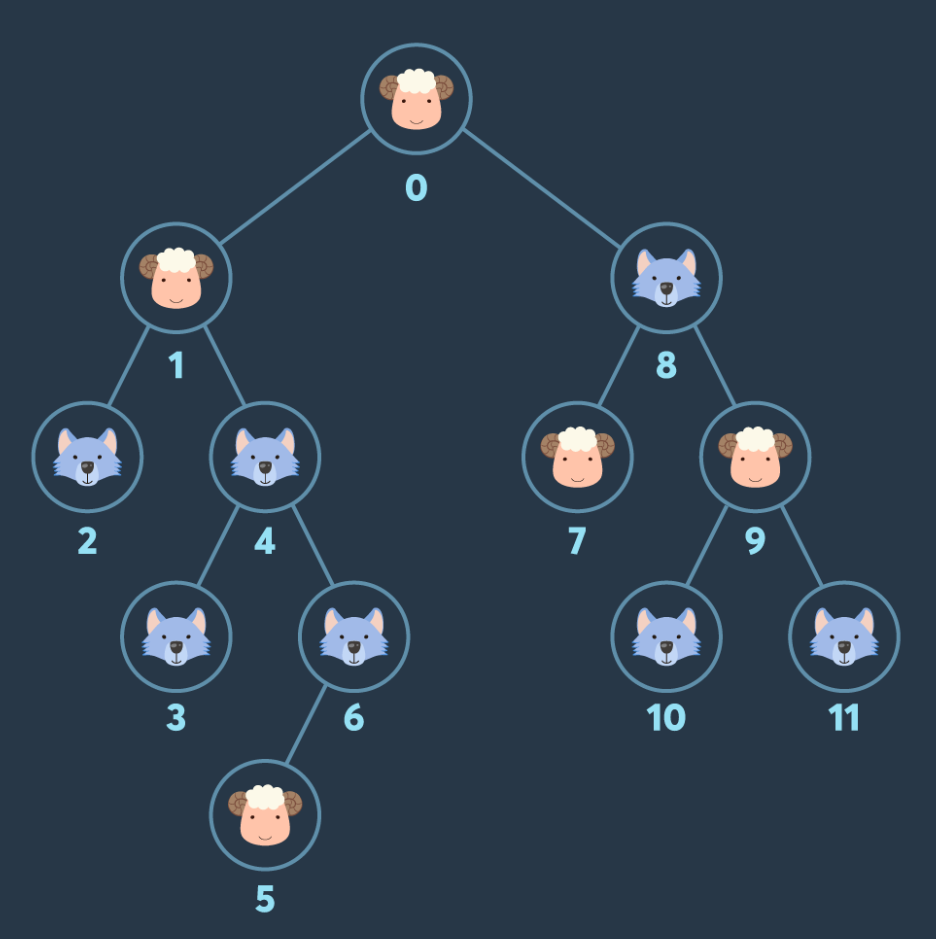
2진 트리 모양 초원의 각 노드에 늑대와 양이 한 마리씩 놓여 있습니다. 이 초원의 루트 노드에서 출발하여 각 노드를 돌아다니며 양을 모으려 합니다. 각 노드를 방문할 때 마다 해당 노드에 있던 양과 늑대가 당신을 따라오게 됩니다. 이때, 늑대는 양을 잡아먹을 기회를 노리고 있으며, 당신이 모은 양의 수보다 늑대의 수가 같거나 더 많아지면 바로 모든 양을 잡아먹어 버립니다. 당신은 중간에 양이 늑대에게 잡아먹히지 않도록 하면서 최대한 많은 수의 양을 모아서 다시 루트 노드로 돌아오려 합니다.

예를 들어, 위 그림의 경우(루트 노드에는 항상 양이 있습니다) 0번 노드(루트 노드)에서 출발하면 양을 한마리 모을 수 있습니다. 다음으로 1번 노드로 이동하면 당신이 모은 양은 두 마리가 됩니다. 이때, 바로 4번 노드로 이동하면 늑대 한 마리가 당신을 따라오게 됩니다. 아직은 양 2마리, 늑대 1마리로 양이 잡아먹히지 않지만, 이후에 갈 수 있는 아직 방문하지 않은 모든 노드(2, 3, 6, 8번)에는 늑대가 있습니다. 이어서 늑대가 있는 노드로 이동한다면(예를 들어 바로 6번 노드로 이동한다면) 양 2마리, 늑대 2마리가 되어 양이 모두 잡아먹힙니다. 여기서는 0번, 1번 노드를 방문하여 양을 2마리 모은 후, 8번 노드로 이동한 후(양 2마리 늑대 1마리) 이어서 7번, 9번 노드를 방문하면 양 4마리 늑대 1마리가 됩니다. 이제 4번, 6번 노드로 이동하면 양 4마리, 늑대 3마리가 되며, 이제 5번 노드로 이동할 수 있게 됩니다. 따라서 양을 최대 5마리 모을 수 있습니다.

각 노드에 있는 양 또는 늑대에 대한 정보가 담긴 배열 info, 2진 트리의 각 노드들의 연결 관계를 담은 2차원 배열 edges가 매개변수로 주어질 때, 문제에 제시된 조건에 따라 각 노드를 방문하면서 모을 수 있는 양은 최대 몇 마리인지 return 하도록 solution 함수를 완성해주세요.

제한 사항

• 2 ≤ info의 길이 ≤ 17
  • info의 원소는 0 또는 1 입니다.
  • info[i]는 i번 노드에 있는 양 또는 늑대를 나타냅니다.
  • 0은 양, 1은 늑대를 의미합니다.
  • info[0]의 값은 항상 0입니다. 즉, 0번 노드(루트 노드)에는 항상 양이 있습니다.
• edges의 세로(행) 길이 = info의 길이 - 1
  • edges의 가로(열) 길이 = 2
  • edges의 각 행은 [부모 노드 번호, 자식 노드 번호] 형태로, 서로 연결된 두 노드를 나타냅니다.
  • 동일한 간선에 대한 정보가 중복해서 주어지지 않습니다.
  • 항상 하나의 이진 트리 형태로 입력이 주어지며, 잘못된 데이터가 주어지는 경우는 없습니다.
  • 0번 노드는 항상 루트 노드입니다.

입출력 예

info edges result
[0,0,1,1,1,0,1,0,1,0,1,1][0,1],[1,2],[1,4],[0,8],[8,7],[9,10],[9,11],[4,3],[6,5],[4,6],[8,9]] 5
[0,1,0,1,1,0,1,0,0,1,0][0,1],[0,2],[1,3],[1,4],[2,5],[2,6],[3,7],[4,8],[6,9],[9,10]] 5

2) 문제 분석 및 풀이

1) 설계, 분석

DFS와 백트레킹을 사용한 완전탐색

2) 풀이

#include <string>
#include <vector>
#include <unordered_map>

using namespace std;
unordered_map<int, vector<int>> tree;
vector<bool> visited;
vector<int> ginfo;
int answer = 0;

void dfs(vector<int> path)
{
    int sheepCnt=0;
    int wolfCnt=0;

    //현재 경로의 늑대와 양의 개수를 종합
    for (auto& p : path)
    {
        if (ginfo[p] == 1) wolfCnt++;
        else sheepCnt++;
    }

    // 늑대가 같거나 많은 경우는 경로 폐기
    if (wolfCnt >= sheepCnt) return;

    // 양의 최댓값 갱신
    answer = max(sheepCnt, answer);

    // 현재 경로에 포함된 노드들을 순회
    // 해당 노드의 인접 노드가 방문 x인 경우
    // 경로에 추가 시키고 새로운 경로로 dfs
    for (int i=0; i<path.size(); i++)
    {
        int p = path[i];
        for (auto& v : tree[p])
        {
            // 이미 방문한 경우 통과 (현재 경로에 포함된 경우)
            if (visited[v]) continue;
            visited[v] = true;
            // 방문하지 않은 인접노드를 경로에 추가하고 DFS
            path.push_back(v);
            dfs(path);
            // v를 넣고 모든 경우의 수를 탐색한 뒤에는
            // v를 미방문 표시
            path.pop_back();
            visited[v] = false;
        }
    }
}

int solution(vector<int> info, vector<vector<int>> edges) {

    ginfo = info;
    visited.resize(info.size());
    // 트리 정보 추가
    // 인접 리스트 형태로 보관
    for (auto& edge : edges)
    {
        tree[edge[0]].push_back(edge[1]);
    }
    visited[0] = true;
    dfs({0});

    return answer;
}

2. 배달

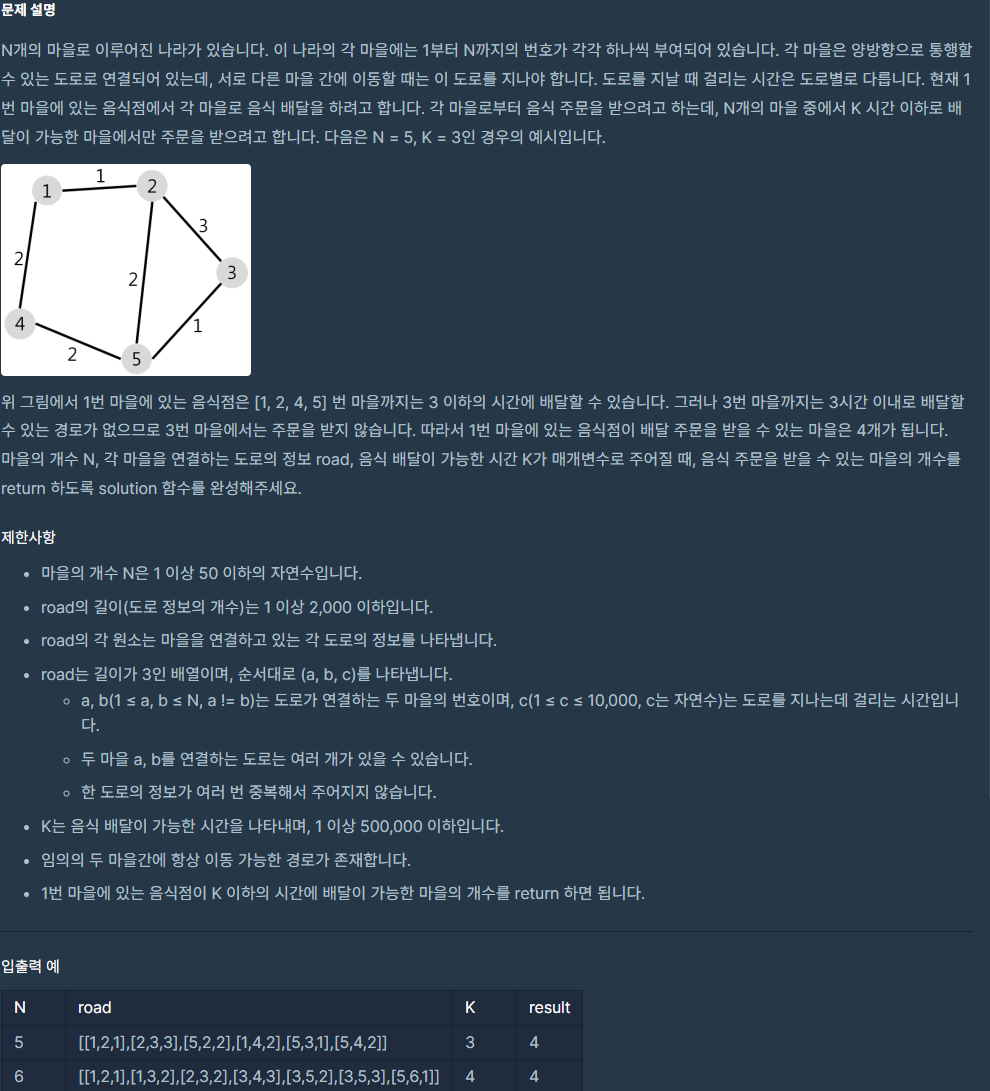
1) 문제

2) 문제 분석 및 풀이

1) 설계, 분석

1번 노드에서 각 노드까지 도달하는 최소 비용을 계산하는 문제
(다익스트라 사용함)

2) 풀이

#include <vector>
#include <unordered_map>
#include <climits>
#include <queue>

using namespace std;

vector<bool> visited;
// 0: minDist, 1: node right before this
vector<vector<int>> dijkstraVec;
unordered_map<int, vector<pair<int,int>>> adjList;

void Dijkstra(int N, int start)
{
    // 초기화
    visited.resize(N+1, false);
    dijkstraVec.resize(N+1, vector<int>(2, INT_MAX));
    // <현재거리, node번호>
    auto cmp = [](const pair<int,int>& a, const pair<int,int>& b){
        return a.first > b.first;
    };
    priority_queue<pair<int, int>, vector<pair<int,int>>, decltype(cmp)> pq(cmp);

    // 1번이 시작노드
    dijkstraVec[start][0] = 0;
    dijkstraVec[start][1] = 1;

    pq.push({0, start});

    while(!pq.empty())
    {
        int nodeNum = pq.top().second;
        int currDist = pq.top().first;
        pq.pop();

        if (visited[nodeNum]) continue;
        visited[nodeNum] = true;
        // start에서 바로 to로 가는것과
        // 중간에 nodeNum 거치는 것 중 작은걸로 갱신
        // u->v와 u->k->v 비교
        for (auto& [to, weight] : adjList[nodeNum])
        {
            //if (visited[to]) continue;
            if (dijkstraVec[to][0] > dijkstraVec[nodeNum][0] + weight)
            {
                dijkstraVec[to][0] = dijkstraVec[nodeNum][0] + weight;
                dijkstraVec[to][1] = nodeNum;
                pq.push({dijkstraVec[to][0], to});
            }
        }
    }
}

int solution(int N, vector<vector<int> > road, int K) {
    int answer = 0;

    for (auto& vec : road)
    {
        // 무방향이라 양쪽 다 추가
        adjList[vec[0]].push_back({vec[1], vec[2]});
        adjList[vec[1]].push_back({vec[0], vec[2]});
    }

    Dijkstra(N, 1);

    // 1번 부터 i까지의 비용이 K이하이면 asnwer증가
    for (int i=1; i<N+1; i++)
    {
        if (dijkstraVec[i][0] <= K) answer++;
    }

    return answer;
}

3. 경주로 건설

1) 문제

문제 설명
건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
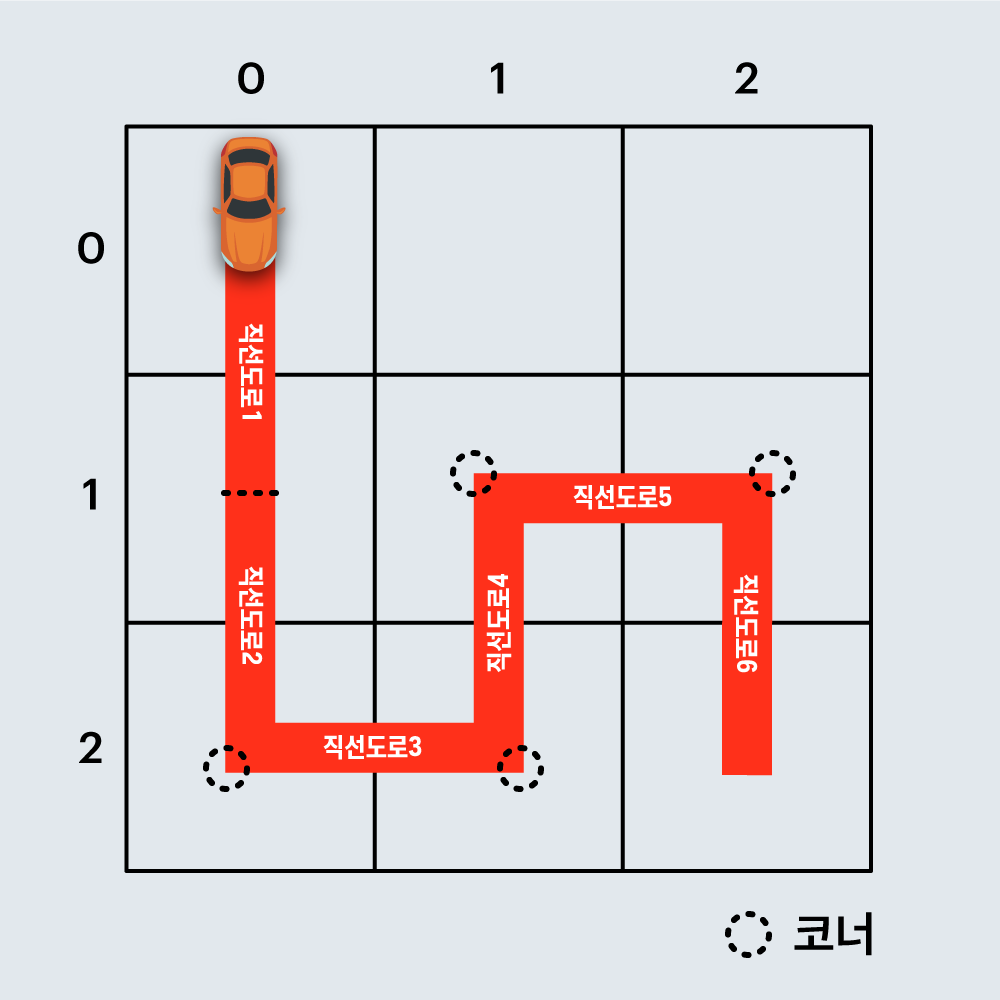
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.

예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.

제한 사항

• board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.

• board 배열의 각 원소의 값은 0 또는 1 입니다.

  • 도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
  • 원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.

• board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.

• 출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.

  입출력 예
  board result
  [[0,0,0],[0,0,0],[0,0,0]] 900
  [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] 3800
  [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] 2100
  [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]] 3200

2) 문제 분석 및 풀이

1) 설계, 분석

BFS에 상태를 추가하는 문제
(다익스트라 사용함)

2) 풀이

#include <string>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

vector<vector<int>> gboard;
vector<vector<vector<int>>> cost;
vector<int> dx = {0, 1, 0, -1};
vector<int> dy = {1, 0, -1, 0};
int N;

enum EDir
{
    RIGHT,
    DOWN,
    LEFT,
    UP,
};

struct Cell
{
    int _x;
    int _y;
    int _cost;
    int _dir;
};

struct CellCmp
{
    bool operator()(const Cell& a, const Cell& b)
    {
        return a._cost > b._cost;
    }
};

bool CanGo(int nx, int ny)
{
    if (nx < 0 || nx >= N) return false;
    if (ny < 0 || ny >= N) return false;
    if (gboard[nx][ny] == 1) return false; 
    return true;
}

void Dijkstra()
{
    cost.resize(N, vector<vector<int>>(N, vector<int>(4,INT_MAX)));
    priority_queue<Cell, vector<Cell>, CellCmp> q;

    // 시작점에서 오른쪽 & 아래 방향으로 초기화
    for (int dir = 0; dir < 2; dir++) {
        int nx = dx[dir], ny = dy[dir];
        if (CanGo(nx, ny)) {
            cost[nx][ny][dir] = 100;
            q.push({nx, ny, 100, dir});
        }
    }

    while(!q.empty())
    {
        Cell front = q.top();
        q.pop();

        int cx = front._x;
        int cy = front._y;
        int ccost= front._cost;
        int dir = front._dir;

        if (cx == N-1 && cy == N-1) continue;

        for (int i=0; i<4; i++)
        {
            int nx = cx + dx[i];
            int ny = cy + dy[i];
            if (CanGo(nx,ny))
            {
                int newCost;
                int newDir = (i);
                // 같은 방향
                if (dir == newDir)
                {
                    newCost = ccost + 100;
                }
                // 90도 회전
                else
                {
                     newCost = ccost + 600;
                }

                if (cost[nx][ny][newDir] > newCost)
                {
                    cost[nx][ny][newDir] = min(cost[nx][ny][newDir], newCost);
                    q.push(Cell({nx,ny,newCost,newDir}));
                }
            }
        }
    }
}

int solution(vector<vector<int>> board) {
    int answer = 0;
    gboard = board;
    N = board.size();
    Dijkstra();

    int minCost = INT_MAX;
    for (int i=0; i<4; i++)
    {
        minCost = min(minCost, cost[N-1][N-1][i]);
    }
    return minCost;
}