알고리즘 스터디 27일차

창고지기·2025년 7월 20일

알고리즘스터디

목록 보기

32/60

1. 피로도

1) 문제

문제 설명
XX게임에는 피로도 시스템(0 이상의 정수로 표현합니다)이 있으며, 일정 피로도를 사용해서 던전을 탐험할 수 있습니다. 이때, 각 던전마다 탐험을 시작하기 위해 필요한 "최소 필요 피로도"와 던전 탐험을 마쳤을 때 소모되는 "소모 피로도"가 있습니다. "최소 필요 피로도"는 해당 던전을 탐험하기 위해 가지고 있어야 하는 최소한의 피로도를 나타내며, "소모 피로도"는 던전을 탐험한 후 소모되는 피로도를 나타냅니다. 예를 들어 "최소 필요 피로도"가 80, "소모 피로도"가 20인 던전을 탐험하기 위해서는 유저의 현재 남은 피로도는 80 이상 이어야 하며, 던전을 탐험한 후에는 피로도 20이 소모됩니다.

이 게임에는 하루에 한 번씩 탐험할 수 있는 던전이 여러개 있는데, 한 유저가 오늘 이 던전들을 최대한 많이 탐험하려 합니다. 유저의 현재 피로도 k와 각 던전별 "최소 필요 피로도", "소모 피로도"가 담긴 2차원 배열 dungeons 가 매개변수로 주어질 때, 유저가 탐험할수 있는 최대 던전 수를 return 하도록 solution 함수를 완성해주세요.

제한 사항

k는 1 이상 5,000 이하인 자연수입니다.

dungeons의 세로(행) 길이(즉, 던전의 개수)는 1 이상 8 이하입니다.

dungeons의 가로(열) 길이는 2 입니다.

dungeons의 각 행은 각 던전의 ["최소 필요 피로도", "소모 피로도"] 입니다.

"최소 필요 피로도"는 항상 "소모 피로도"보다 크거나 같습니다.

"최소 필요 피로도"와 "소모 피로도"는 1 이상 1,000 이하인 자연수입니다.

서로 다른 던전의 ["최소 필요 피로도", "소모 피로도"]가 서로 같을 수 있습니다.

입출력 예
k dungeons result
80 [[80,20],[50,40],[30,10]] 3

2) 문제 분석 및 풀이

1) 설계, 분석

백트래킹의 문제

2) 풀이

#include <string>
#include <vector>
#include <iostream>
using namespace std;

vector<vector<int>> Gdungeons;
vector<bool> visited;
int answer = -1;
int N;
using namespace std;

void dfs(int k, int depth)
{
    // 기저 조건 모든 노드를 방문, 해당 경로에서 더이상 갈 수 없는 경우
    // 종료되어 백트래킹
    answer = max(answer, depth);
    for (int i=0; i<N; i++)
    {
        // 던전을 돌면서 이미 방문한 던전이면 지나감
        // 해당 던전의 요구 피로도가 K보다 크면 지나감(방문 불가)
        if (visited[i]) continue;
        if (k < Gdungeons[i][0]) continue;

        // 조건의 맞는 노드를 방문
        // i의 소모 피로도를 k에서 뺀 값으로 dfs 진행
        visited[i] = true;
        dfs(k - Gdungeons[i][1], depth+1);
        visited[i] = false;
    }
}

int solution(int k, vector<vector<int>> dungeons) {
    Gdungeons = dungeons;
    N = dungeons.size();
    visited.resize(N,false);
    dfs(k,0);
    return answer;
}

2. N-Queen

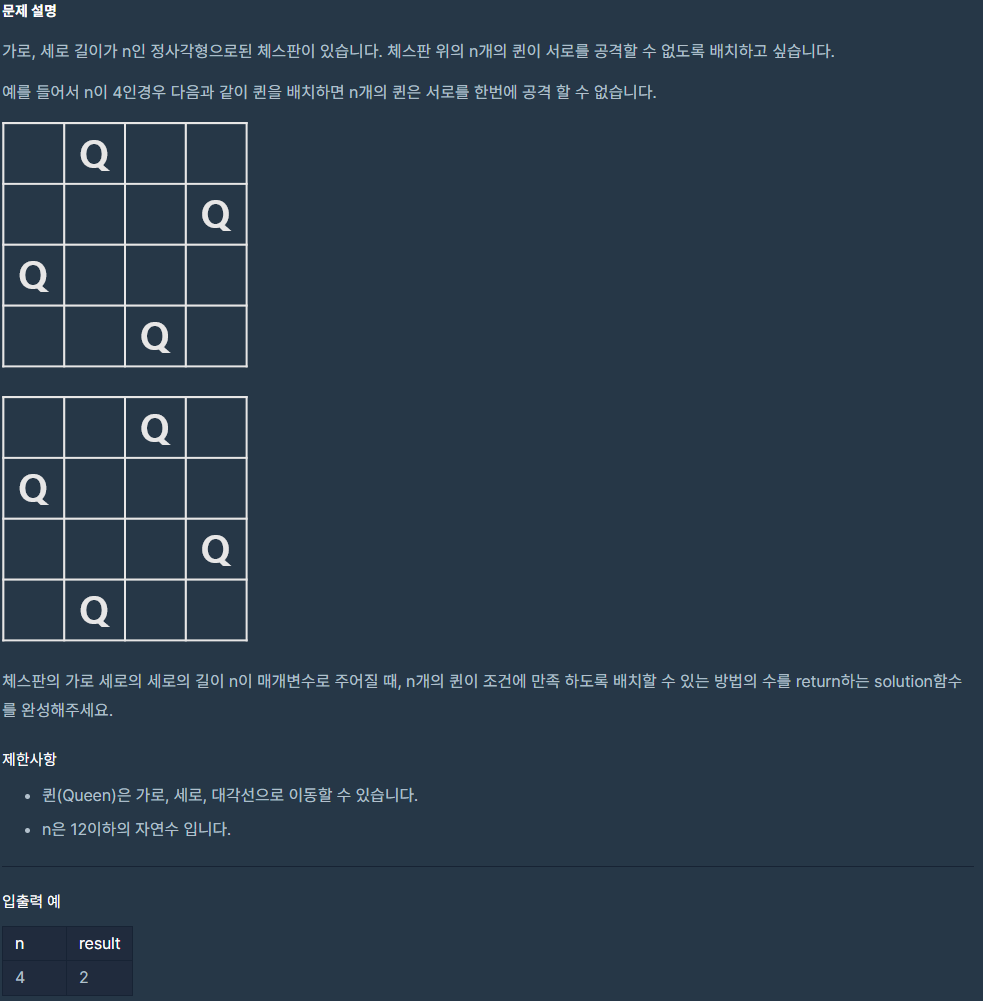
1) 문제

2) 문제 분석 및 풀이

1) 설계, 분석

브루트포스 백트레킹에 사용하는 전형적이 예시

2) 풀이

#include <string>
#include <vector>
using namespace std;

vector<vector<bool>> board;
int N;
int answer;
bool PlaceQueen(int x, int y)
{
    //열 체크 (행은 이미 dfs구조에서 확인)
    for (int i = 0 ; i<N; i++)
    {
        if (board[i][y] == true) return false;
    }
 
    //왼쪽 대각선
    //좌상향 방향만 체크 (로직상 가장 밑에 놓여질 퀸이기 때문에)
    int nx = x;
    int ny = y;
    while (true)
    {
        nx--;
        ny--;
        if (nx < 0|| ny < 0) break;
        if (board[nx][ny] == true) return false;
    }

    //오른쪽 대각선
    //우상향 방향만 체크 (로직상 가장 밑에 놓여질 퀸이기 때문에)
    nx = x;
    ny = y;
    while (true)
    {
        nx--;
        ny++;
        if (nx < 0 || ny >= N) break;
        if (board[nx][ny] == true) return false;
    }

    return true;
}

void dfs(int row, int num)
{
    // 기저 조건
    // 퀸을 N개 배치하면 종료
    if (num == N)
    {
        answer++;
        return;
    }

    // 각 row에는 퀸을 하나만 놓을 수 있으니
    // 각 Cell을 볼것이 아니라 row 기준으로 백트래킹
    // 0.현재 row에 퀸을 배치할 수 있는지 확인
    //   0-1 놓을 수 있으면 놓고 다음 row로 dfs;
    for (int i=0; i<N; i++)
    {
        if (board[row][i] == false)
        {
            if (PlaceQueen(row, i))
            {
                board[row][i] = true;
                dfs(row + 1 , num + 1);
                board[row][i] = false;
            }
        }
    }
}

int solution(int n) {
    board.resize(n, vector<bool>(n, false));
    N = n;
    dfs(0, 0);

    return answer;
}