알고리즘 스터디 48일차

1. 예산

1) 문제

S사에서는 각 부서에 필요한 물품을 지원해 주기 위해 부서별로 물품을 구매하는데 필요한 금액을 조사했습니다. 그러나, 전체 예산이 정해져 있기 때문에 모든 부서의 물품을 구매해 줄 수는 없습니다. 그래서 최대한 많은 부서의 물품을 구매해 줄 수 있도록 하려고 합니다.

물품을 구매해 줄 때는 각 부서가 신청한 금액만큼을 모두 지원해 줘야 합니다. 예를 들어 1,000원을 신청한 부서에는 정확히 1,000원을 지원해야 하며, 1,000원보다 적은 금액을 지원해 줄 수는 없습니다.

부서별로 신청한 금액이 들어있는 배열 d와 예산 budget이 매개변수로 주어질 때, 최대 몇 개의 부서에 물품을 지원할 수 있는지 return 하도록 solution 함수를 완성해주세요.

제한사항
d는 부서별로 신청한 금액이 들어있는 배열이며, 길이(전체 부서의 개수)는 1 이상 100 이하입니다.
d의 각 원소는 부서별로 신청한 금액을 나타내며, 부서별 신청 금액은 1 이상 100,000 이하의 자연수입니다.
budget은 예산을 나타내며, 1 이상 10,000,000 이하의 자연수입니다.

입출력 예
입출력 예
d budget result
[1,3,2,5,4] 9 3
[2,2,3,3] 10 4

2) 문제 분석 및 풀이

1) 설계, 분석

2) 풀이

#include <vector>
#include <algorithm>

using namespace std;

int solution(vector<int> d, int budget) 
{
    int answer = 0;

    sort(d.begin(), d.end());

    for (auto& e : d)
    {
        if (e > budget) break;
        budget -= e;
        answer++;
    }

    return answer;
}

2. 구명 보트

1) 문제

무인도에 갇힌 사람들을 구명보트를 이용하여 구출하려고 합니다. 구명보트는 작아서 한 번에 최대 2명씩 밖에 탈 수 없고, 무게 제한도 있습니다.

예를 들어, 사람들의 몸무게가 [70kg, 50kg, 80kg, 50kg]이고 구명보트의 무게 제한이 100kg이라면 2번째 사람과 4번째 사람은 같이 탈 수 있지만 1번째 사람과 3번째 사람의 무게의 합은 150kg이므로 구명보트의 무게 제한을 초과하여 같이 탈 수 없습니다.

구명보트를 최대한 적게 사용하여 모든 사람을 구출하려고 합니다.

사람들의 몸무게를 담은 배열 people과 구명보트의 무게 제한 limit가 매개변수로 주어질 때, 모든 사람을 구출하기 위해 필요한 구명보트 개수의 최솟값을 return 하도록 solution 함수를 작성해주세요.

제한사항
무인도에 갇힌 사람은 1명 이상 50,000명 이하입니다.
각 사람의 몸무게는 40kg 이상 240kg 이하입니다.
구명보트의 무게 제한은 40kg 이상 240kg 이하입니다.
구명보트의 무게 제한은 항상 사람들의 몸무게 중 최댓값보다 크게 주어지므로 사람들을 구출할 수 없는 경우는 없습니다.

입출력 예
people limit return
[70, 50, 80, 50] 100 3
[70, 80, 50] 100 3

2) 문제 분석 및 풀이

1) 설계, 분석

2) 풀이

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

int solution(vector<int> people, int limit) 
{
    int answer = 0;
    int left=0, right=people.size()-1;

    sort(people.begin(), people.end());

    // 남은 거 중에 가장 큰거 넣고, 남은공간에 제일 작은거 부터 넣어봄
    // 남은 공간이 제일 적게!
    while(left <= right)
    {
        // 제일 큰거 넣고, 작은거 들어가면 넣음.
        if (people[left] <= limit - people[right--])
            left++;

        answer++;
    }

    return answer;
}

3. 귤 고르기

1) 문제

경화는 과수원에서 귤을 수확했습니다. 경화는 수확한 귤 중 'k'개를 골라 상자 하나에 담아 판매하려고 합니다. 그런데 수확한 귤의 크기가 일정하지 않아 보기에 좋지 않다고 생각한 경화는 귤을 크기별로 분류했을 때 서로 다른 종류의 수를 최소화하고 싶습니다.

예를 들어, 경화가 수확한 귤 8개의 크기가 [1, 3, 2, 5, 4, 5, 2, 3] 이라고 합시다. 경화가 귤 6개를 판매하고 싶다면, 크기가 1, 4인 귤을 제외한 여섯 개의 귤을 상자에 담으면, 귤의 크기의 종류가 2, 3, 5로 총 3가지가 되며 이때가 서로 다른 종류가 최소일 때입니다.

경화가 한 상자에 담으려는 귤의 개수 k와 귤의 크기를 담은 배열 tangerine이 매개변수로 주어집니다. 경화가 귤 k개를 고를 때 크기가 서로 다른 종류의 수의 최솟값을 return 하도록 solution 함수를 작성해주세요.

제한사항
1 ≤ k ≤ tangerine의 길이 ≤ 100,000
1 ≤ tangerine의 원소 ≤ 10,000,000

입출력 예
k tangerine result
6 [1, 3, 2, 5, 4, 5, 2, 3] 3
4 [1, 3, 2, 5, 4, 5, 2, 3] 2
2 [1, 1, 1, 1, 2, 2, 2, 3] 1

2) 문제 분석 및 풀이

1) 설계, 분석

2) 풀이

#include <string>
#include <vector>
#include <unordered_map>
#include <algorithm>

using namespace std;

int solution(int k, vector<int> tangerine) 
{
    unordered_map<int, int> typeCnt;
    int answer = 0;

    // 각 종류가 몇개 있는지 확인
    for (int i=0; i<tangerine.size(); i++)
    {
        typeCnt[tangerine[i]]++;
    }

    // 몇개인지 벡터에 넣음 (종류는 필요없음)
    vector<int> typeVec;
    for (auto& cnt : typeCnt)
    {
        typeVec.push_back(cnt.second);
    }

    // 내림차순
    sort(typeVec.begin(), typeVec.end(), greater<>());

    // 부분 배낭처럼 제한보다 크면 제한 만큼만 넣음
    for (auto& cnt : typeVec)
    {
        answer++;
        if (cnt >= k) break;
        k -= cnt;
    }

    return answer;
}

4. 기지국 설치

1) 문제

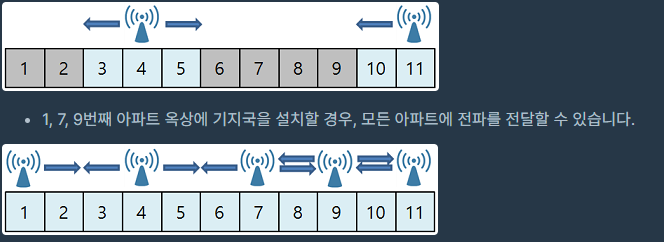
N개의 아파트가 일렬로 쭉 늘어서 있습니다. 이 중에서 일부 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 기술이 발전해 5g 수요가 높아져 4g 기지국을 5g 기지국으로 바꾸려 합니다. 그런데 5g 기지국은 4g 기지국보다 전달 범위가 좁아, 4g 기지국을 5g 기지국으로 바꾸면 어떤 아파트에는 전파가 도달하지 않습니다.

예를 들어 11개의 아파트가 쭉 늘어서 있고, [4, 11] 번째 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 만약 이 4g 기지국이 전파 도달 거리가 1인 5g 기지국으로 바뀔 경우 모든 아파트에 전파를 전달할 수 없습니다. (전파의 도달 거리가 W일 땐, 기지국이 설치된 아파트를 기준으로 전파를 양쪽으로 W만큼 전달할 수 있습니다.)

이때, 우리는 5g 기지국을 최소로 설치하면서 모든 아파트에 전파를 전달하려고 합니다. 위의 예시에선 최소 3개의 아파트 옥상에 기지국을 설치해야 모든 아파트에 전파를 전달할 수 있습니다.

아파트의 개수 N, 현재 기지국이 설치된 아파트의 번호가 담긴 1차원 배열 stations, 전파의 도달 거리 W가 매개변수로 주어질 때, 모든 아파트에 전파를 전달하기 위해 증설해야 할 기지국 개수의 최솟값을 리턴하는 solution 함수를 완성해주세요

제한사항
N: 200,000,000 이하의 자연수
stations의 크기: 10,000 이하의 자연수
stations는 오름차순으로 정렬되어 있고, 배열에 담긴 수는 N보다 같거나 작은 자연수입니다.
W: 10,000 이하의 자연수

입출력 예
N stations W answer
11 [4, 11] 1 3
16 [9] 2 3

2) 문제 분석 및 풀이

1) 설계, 분석

2) 풀이

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

int W;
int PlaceStationInRange(int left, int right)
{
    double res = 0;
    // 전파가 닿지 않는 영역
    int uncoveredLen = (right - left + 1) * 1.0f;

    // left, right 사이의 모든 영역에 전파가 들어오는 경우 종료
    if (uncoveredLen < 0) return 0;

    // 기지국이 커버하는 영역은 양쪽으로 W, 설치된자리 -> 2W+1이다.
    // 전파가 닿지 않는 영역의 크기를 2W+1로 나눈뒤 올림 처리하면 설치 해야힐 기지국의 최솟값이 나온다
    // 나눈 몫이 정수가 아니다 -> 모든 영역을 커버하지 못한다. -> 1개 더 설치한다.
    res += ceil(uncoveredLen/(2*W + 1.0f));

    return res;
}

int solution(int n, vector<int> stations, int w)
{
    int answer = 0;
    W=w;

    // 1부터 처음 기지국까지 건설해야하는 개수
    answer+= PlaceStationInRange(1, (stations[0] - w - 1));

    // i-1 기지국에서 i 기지국 사이에 건설해야하는 기지국 수
    for (int i=1; i<stations.size(); i++)
        answer+= PlaceStationInRange((stations[i-1]+w+1), (stations[i] - w - 1));

    // N에서 마지막 기지국까지 건설해야하는 개수
    answer+= PlaceStationInRange((stations.back()+w + 1), n);

    return answer;
}