[LeetCode] 743. Netword Delay Time

https://leetcode.com/problems/network-delay-time/

---

접근 방법: Dijkstra's Algorithm

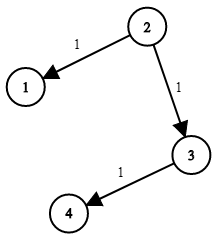
• k노드가 다른 모든 노드와 연결되어 있다면 최장 경로의 값을 반환하고, 아닐 경우 -1을 반환한다.
• 최단 거리 탐색과 관련된 문제이므로 다익스트라 알고리즘을 활용할 수 있다.

코드: 교재

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        def dijkstra(start):
            pq = [(0, start)]
            dist = collections.defaultdict(int)

            while pq:
                acc, cur = heapq.heappop(pq)
                if cur not in dist:
                    dist[cur] = acc  
                    for adj, t in graph[cur]:
                        time = acc + t
                        # 새로운 time값을 체크하지 않고 모두 큐에 추가 -> O(logN)
                        heapq.heappush(pq, (time, adj))
            return dist

        graph = collections.defaultdict(list)
        for p, q, d in times:
            graph[p].append((q, d))

        dist = dijkstra(k)
        return max(dist.values()) if len(dist) == n else -1

• 위 코드는 교재에 있던 코드를 가져온 것인데, defaultdict을 이용하여 딕셔너리로 다익스트라 함수의 결과값을 저장한다.
• 힙 큐는 매 번 최단 경로의 노드를 가져오므로, 위와 같이 dist의 키 리스트에 해당 노드가 들어있지 않을 때에만 for문을 실행시키더라도 모든 노드의 최단 경로를 가져올 수 있다. 단, for문의 말미에 다음 노드로의 모든 경로를 전부 heappush하게 되는데, 이 때 이미 방문했던 노드에 대해서도 전부 heappush를 하게 되어 필요없는 데이터도 추가하게 된다. heappush가 $O(logN)$의 시간복잡도를 가지므로 위 코드에서 heappush를 하기 전에 해당되는 노드가 가지고있는 time값과 비교하여 작을 경우에만 heap push를 시행하게 하면 런타임이 크게 줄어들 것이라고 생각했다.

---

코드: 1차 수정

        def dijkstra(start):
            pq = [(0, start)]
            dist = collections.defaultdict(int)

            while pq:
                acc, cur = heapq.heappop(pq)
                # for문 안의 if문 때문에 요소가 생성되어버림
                if cur not in dist:
                    dist[cur] = acc  
                    for adj, t in graph[cur]:
                        time = acc + t
                        # 딕셔너리에서 값을 비교 후 필요한 데이터만 heappush
                        if time < dist[adj]:
                            heapq.heappush(pq, (time, adj))
            return dist

• 위와 같이 수정 후 실행시켰는데, 에러가 발생하였다. 에러가 발생한 원인은 추가한 if 조건문에서 dist의 요소를 체크하게 되는데, 이 때 아직 방문하지 않은 노드들도 모두 체크하게 되어 0값을 가지는 요소쌍이 추가되어 버린 것이다.
• 그래서 교재처럼 defaultdict의 성질을 이용하는 방법 대신 visited() 세트를 만들어 방문했던 노드를 저장하기로 하였다. 또한 defaultdict로 초기값을 지정해주어 조건문에서 잘못 넘어가는 일이 없도록 수정했다.

---

코드: 2차 수정

        def dijkstra(start):
            dist = collections.defaultdict(lambda: int(1e9))
            pq = []
            heapq.heappush(pq, (0, start))
            dist[start] = 0
            visited = set()

            while pq:
                acc, cur = heapq.heappop(pq)

                if cur in visited:
                    continue                    
                visited.add(cur)
                # if dist[cur] < acc:
                #     continue

                for adj, d in graph[cur]:                 
                    time = acc + d
                    if time < dist[adj]:
                        dist[adj] = time
                        heapq.heappush(pq, (time, adj))

            return dist

• 런타임이 확 줄어든 것을 확인했다.
• 중복방문에 대한 처리는 visited() 세트를 만들어서 구별했는데, 강의에서 했던 방식처럼 딕셔너리의 값을 대조하는 방법도 똑같은 시간복잡도를 가지므로 어느 방식을 사용해도 될 것 같다.

---

전체 코드

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        def dijkstra(start):
            dist = collections.defaultdict(lambda: int(1e9))
            pq = []
            heapq.heappush(pq, (0, start))
            dist[start] = 0

            while pq:
                acc, cur = heapq.heappop(pq)
                if dist[cur] < acc:
                    continue

                for adj, d in graph[cur]:
                    time = acc + d
                    if time < dist[adj]:
                        dist[adj] = time
                        heapq.heappush(pq, (time, adj))

            return dist

        graph = collections.defaultdict(list)
        for p, q, d in times:
            graph[p].append((q, d))

        ret = dijkstra(k)
        return max(ret.values()) if len(ret) == n else -1

• 만약 k노드와 모든 노드가 연결되어 있다면, 다익스트라 함수가 반환한 딕셔너리의 길이가 전체 노드 갯수만큼 존재할 것이므로 len()을 이용하여 체크하였다.