앞서 배운 탐욕 알고리즘과 늘 함께 언급되는 Dynamic Programming ( 동적 계획법 ) 이 있다.
탐욕알고리즘 , 다이나믹 프로그래밍 모두 작은문제에서 출발한다는 점은 같지만, 탐욕 알고리즘이 순간의 최적을 찾는 방식이라면 , 다이나믹프로그래밍은 모든경우의 수를 따져본 후 이를 조합해 최적의 해법을 찾는 방식이다.
다이나믹 프로그래밍의 원리는 간단하다. 주어진 문제를 여러개의 하위문제로 나누어풀고, 하위문제들의 해결방법을 결합하여, 최종 문제를 해결하는 문제 해결방식이다. 하위문제를 계산하고 그 해결책을 저장하고 나중에 같은 하위문제가 나왔을때 저장된 해결책을 이용해서 비효율적인 알고리즘을 개선하는 방법이다.
즉, 하나의 문제는 단 한번만 풀도록 하는 알고리즘이 바로 다이나믹 프로그래밍이다.
다이나믹 프로그래밍은 두가지 가정이 만족하는 조건에서 사용가능하다.
- 큰 문제를 작은 문제로 나눌수 있고, 이 작은 문제들이 중복된다. (Overlapping Sub-problems)
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 즉 , 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다.(Optimal Substructure)
그렇다면 이 두 가지 조건이 의미하는 바에 대해 조금 더 깊이 확인 해보자.
첫번째 조건인 큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제들은 중복된다 (Overlapping Sub-problems) 는 바꿔말하면 큰 문제로부터 나누어진 작은 문제는 큰 문제를 해결할때 여러번 반복해서 사용될 수 있어야한다 라고 말할수 있다. 이를 확인하기 위해 피보나치 수열을 예로 들면
피보나치 수열은 첫째와 둘째항이 1이며 , 그 뒤의 모든 항이 바로 앞 두항의 합이 수열, 이를 재귀함수를 사용해서 구현하면 간단히 아래처럼된다.
function fib(n) {
if(n<=2)return 1;
return fib(n-1) + fib(n-2);
// 1,1,2,3,5,8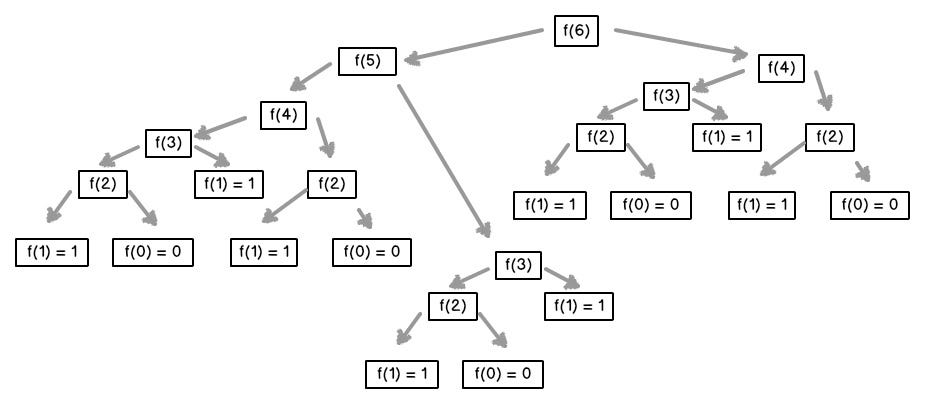
6번째 피보나치수 fib(6)를 구하는 과정은
fib(6) = fib(5) + fib(4)
fib(5) = fib(4) + fib(3)
fib(4) = fib(3) + fib(2)
....
위와 같이 동일한 계산을 반복적으로 수행해야 하고, 이 과정 안에서 fib(4)는 두번 , fib(3)은 세번
fib(2)는 다섯번 동일한계산을 반복해야하는것을 확인할 수있다.
이처럼 작은 문제의 결과를큰 문제를 해결하기 위해 여러번 반복하여 사용할 수 있을때 부분 문제의 반복(Overlapping Sub-problems)이라는 조건을 만족한다고 볼수 있다.
하지만 이 조건이 만족하는지 확인 하기 전에 주의해야할점이 있다.
주어진 문제를 단순히 반복 계산하여 해결하는것이 아니라 작은문제의 결과가 큰 문제를 해결하는데에 여러번 사용될수 있어야한다는점이다.
이번에는 두번째 조건인 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다(Optimal solution)을 의미한다. 따라서 두번째 조건을 달리 표현하면 주어진 문제에 대한 최적의 해법을 구하고자 할때, 그것의 작은 문제들의 최적의 해법(Optomal solution of Sub-problems)을 찾은 후 그것들을 결합하면 결국 전체 문제의 최적의 해법(Optimal solution)을 구할 수 있다. 라고 할 수 있다.
Recursion + Memoization
다이나믹 프로그래밍을 이용해서 피보나치 수열 문제를 다시 한번 해결해보자.
도입부에서 다이나믹 프로그래밍은 하위 문제의 해결책을 저장한 뒤 동일 한 하위문제가 나왔을 경우 저장해 놓은 해결책을 이용한다고 했다.
Memoization의 정의는 컴퓨터 프로그램이 동일한 계산을 반복해야할때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복수행을 제거하여 프로그램 실행속도를 빠르게하는 기술 이다.
이제 재귀함수에 과연 Memorization을 어떻게 적용할지 함께 확인해 보자.
function fibMemo(m,memo = []){
if(memo[n] !== undefined) return memo[n];
//이미 해결한 하위 문제인지 찾아본다
if(n<=2) return 1;
let res = fibMemo(n-1,memo) + fibMemo(n-2,memo);
memo(n) = res;
return res;
fibmemo(6)의 경우
딱 한번의 6,5,4,3,2 ... 를 통해서 memo에 전부 저장되므로
6번만 계산하면 그뒤로 연산이없다.
즉
big-O 표현식으로는 O(n)의 시간 복잡도를 가진다.
원래 리커시브한 피보나치의경우는 매우 시간복잡도가 높은 O(2ⁿ) 이라는점을 고려하면
다이나믹 프로그래밍의 강점을 확인 할수있다.
마치 위에서 아래로 내려가는것처럼 큰문제를 해결하기 위해 작은문제를 호출한다고 하여서
이 방식을 Top-Down 방식이라고 부르기도 한다.
Iteration + Tabulation
앞서 재귀함수를 이용하였다면 이번에는 반복문을 이용하여 다이나믹 프로그래밍을 구현해보자.
하위 문제의 결괏값을 배열에 저장해놓고, 필요한 시 꺼내 사용하는 개념은 재귀함수를 이용한 방법과 같지만,
재귀함수를 이용한 방법은 문제를 해결하기 위해 큰 문제부터 시작하여 작은 문제로 옮아 가며 문제를 해결하였다면,
반복문을 이용한 방법은 작은 문제에서부터 시작하여 큰 문제를 해결해 나가는 방법ㅇ이다. 그때문에
이를 Bottom-up 방식이라 부르기도 한다.
function fibTab(n){
if(n<=2)return 1;
let fibNum = [0,1,1];
// n 이 1 & 2 일때의 값을 미리 배열에 저장해 놓는다.
for(let i=3; i<= n ; i++){
fibNum[i] = fibNum[i-1] + fibNum[i-2];
// n>=3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여
// n번째 피보나치수를 구한뒤 배열에 저장후 리턴한다.
}
return fibNum[n]
크롬 개발자 도구에서 함수 실행시간 측정 방법
var t0 = performance.now();
fib(50); // 여기에서 함수 실행을 시켜주세요
var t1 = performance.now();
console.log("runtime: " + (t1 - t0) + 'ms')
