탐색(Search)이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 말한다.
대표적인 그래프 탐색 알고리즘으로는 DFS / BFS가 있다.
코테에서 매우 많이 자주 등장한다.
알기전에 먼저 사전에 숙지해야할 데이터 자료형
자료구조
자료구조 : 스택 Stack
- 먼저 들어온 데이터가 나중에 나가는 형식(선입후출)의 자료구조 입니다.
- 입구와 출구가 동일한 형태로 스택을 시각화할 수 있다.
( 주로 박스 쌓기 예시, 위에를 들어내지않으면 중간것이나 아래것을 빼기 힘드므로 위에부터 빼게됨 )
스택의 동작 예시
- 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
5 2 3 7 까지들어오고 삭제해서 7이 나가게됨
5 2 3 에서 다시 삽입 1, 4 들어온다
5 2 3 1 4 에서 마지막 4를 삭제 하게된다.
5 2 3 1 이된다.
나는 주로 JS를 사용하지만 , Python에서는 List자료형자체가 스택자료구조를 활용하기에 적합하다. (별도의 라이브러리가 필요없다)
자료구조 : 큐 Queue
먼저 들어온 데이터가 먼저 나가는 형식(선입선출)의 자료구조이다.
큐는 입구와 출구가 모두 뚫려 있는 터널과 같은 형태로 시각화 할수있다.
보통 은행창구등에 비유해볼수있고, 대기열등을 생각하면 이해가 쉽다.
큐의 동작 예시
- 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
파이프라인 처럼 생각하면 조금더 편하다.
5가 들어오고
2 / 5 가 들어오고
3 / 2 / 5 이렇게 왼쪽에서 들어온다고하면 (사실 방향은 본인이 이해하기 나름 ;)
7 / 3 / 2 / 5 이렇게 파이프라인에 들어와있다면 방향이 왼쪽이라면
먼저들어온 5가 먼저 빠져나가야 큐 자료구조의 특성을 만족한다.
그래서 삭제명령이 실행되었을때
5가 나가서
7 3 2 가 남게되고 이후 삽입하면 다시 왼쪽 (즉 들어오는 입구)에 추가된다.
1 7 3 2
4 1 7 3 2
에서 다시 삭제 명령으로
2가 빠져나가서
4 1 7 3 이 마지막 파이프라인에 남게 된다. (실제로 파이프라인이라는 표현을 쓰는 몇몇 서비스? 들을 다루게될수있는데, 주로 큐처럼 동작하게되므로 거의 같은 의미로 사용된다고 보면될꺼같다.)
또 파이썬에 대한 팁을 주자면
from collections import deque deque 라이브러리를 사용하도록 하자,
List 자료형을 써도 큐를 구현할수있지만, 시간복잡도가 더 높아서 비효율적일수있다.
그래서 덱? 라이브러리를 쓰는걸 추천한다.
" 엄밀히 말하면 덱 라이브러리는 스택과 큐 자료구조의 장점을 모두 합친 형태의 자료구조이다 "
시간복잡도 : 상수시간
append , popleft를 사용하는게 파이썬 이용자들간의 관행처럼 통용된다.
재귀함수
- 재귀 함수(Recursive Function)란 자기 자신을 다시 호출하는 함수를 의미한다.
- 단순한 형태의 재기 함수 예제
- "재귀 함수를 호출합니다." 라는 무자열을 무한히 출력한다.
- 어느정도 출력하다가 최대 재귀 깊이 초과 메시지가 출력된다.
어느정도 코딩을 하다보면,
리컬시브(발음..?)에 대해서 많이 듣게된다.
개인적으로는 어떤 구현에 있어서, 재귀적으로 구현하는일이 나는 없었다.
하지만, 웹개발에 있어서 항상 뒤로가면갈수록, 성능최적화(optimization) 를 할 수 있다는 역량의 중요성이 생므로, 신입개발자에게는 상대적으로 적은 기량요구가 될수있으나,
결국 아는 만큼 보인다.
재귀함수의 종료 조건
- 재귀 함수를 문제 풀이에서 사용할 때는 재귀 함수의 종료 조건을 반드시 명시해야 합니다.
- 종료 조건을 제대로 명시하지 않으면 함수가 무한히 호출될 수 있습니다.
- 종료 조건을 포함한 재귀 함수 예제
function recursive(i) {
// 100번째 호출을 했을 때 종료되도록 종료 조건 명시
if(i===100) {
return;
}
console.log(`${i}번째 재귀함수에서 ${i + 1}번째 재귀함수를 호출합니다.`);
recursive(i + 1);
console.log(`${i}번째 재귀함수를 종료합니다.`);
}
recursive(1)
// 결과 예측
// 1번째 재귀함수에서 2번째 재귀함수를 호출합니다.
// 2번째 재귀함수에서 3번째 재귀함수를 호출합니다.
// 3번째 재귀함수에서 4번째 재귀함수를 호출합니다.
// .....(중략)
// 99번째 재귀함수에서 100번째 재귀함수를 호출합니다.
// -------이때가 종료조건 if를 충족하므로 return 되면서
// 99번째 재귀함수를 종료합니다.
// 98번째 재귀함수를 종료합니다.
// 97번째 재귀함수를 종료합니다.
// .....(중략)
// 1번째 재귀함수를 종료합니다.
팩토리얼 구현 예제
- n! = 1x2x3x ... x (n-1) x n
- 수학적으로 0! 과 1! 의 값은 1입니다.
function factorial_iterative(n) {
let result = 1;
// 1부터 n까지의 수 차례대로 곱하기
for(let i=0; i<n+1; i++) {
result *= i; // result = result * i ;
}
return result;
}
function factorial_recursive(n) {
if(n<=1) { // n이 1이하인 경우 1을 반환
return 1;
}
// n! = n * (n-1)!를 그대로 코드로 작성하기
return n * factorial_recursive(n - 1)
}
factorial_iterative(5) //120
factorial_recursive(5) //120최대공약수 계산 (유클리드 호제법) 예제
-
두 개의 자연수에 대한 최대공약수를 구하는 대표적인 알고리즘으로는 유클리드 호제법이 있습니다.
-
유클리드 호제법
- 두 자연수 A,B에 대하여 (A>B) A를 B로 나눈 나머지를 R이라고 합시다.
- 이때 A와 B의 최대공약수는 B와 R의 최대공약수와 같습니다.
-
유클리드 호제법의 아이디어를 그대로 재귀 함수로 작성할 수 있습니다.
- 예시 : GCD(192, 162)
| 단계 | A | B |
|---|---|---|
| 1 | 192 | 162 |
| 2 | 162 | 30 |
| 3 | 30 | 12 |
| 4 | 12 | 6 |
function GCD(a, b) {
if(a%b===0) {
return b;
}else{
return GCD(b, a%b);
}
}
console.log(GCD(192, 162)) // 6
재귀 함수 사용의 유의 사항
- 재귀함수를 잘 활용하면 복잡한 알고리즘을 간결하게 작성할 수 있습니다.
- 단, 오히려 다른 사람이 이해하기 어려운 형태의 코드가 될 수도 있으므로 신중하게 사용해야 합니다.
- 모든 재귀 함수는 반복문을 이용하여 동일한 기능을 구현할 수 있습니다.
- 재귀 함수가 반복문보다 유리한 경우도 있고 불리한 경우도 있습니다.
- 컴퓨터가 함수를 연속적으로 호출하면 컴퓨터 메모리 내부의 스택 프레임이 쌓입니다.
- 그래서 스택을 사용해야 할 때 구현상 스택 라이브러리 대신에 재귀함수를 이용하는 경우가 많습니다.
- 위 특성때문에 대표적으로 DFS를 더욱더 간결하고 짧은 코드로 작성하기 위해서 단순히 재귀함수를 이용해서 DFS를 구현하곤 한다.
DFS
DFS(Depth-First Search)
- DFS는 깊이 우선 탐색이라고도 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘입니다.
- DFS는 스택 자료구조(혹은 재귀 함수)를 이용하며, 구체적인 동작 과정은 다음과 같습니다.
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 합니다.
- 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리합니다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼냅니다.
- 더 이상 2번의 과정을 수핼할 수 없을 때까지 반복합니다.
동작 예시
- [Step 0] 그래프를 준비합니다. (방문 기준 : 번호가 낮은 인접 노드 부터)
- 시작 노드 : 1
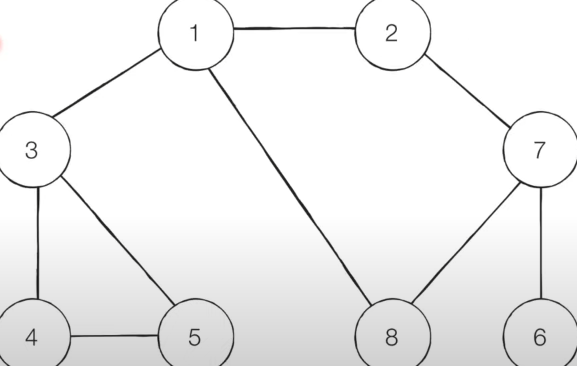
일단 간선은 방향이없는 무방향 그래프 이며,
어떤 노드부터 방문해야할까? 기준 = 문제에서 요구하는 내용에따라서 조금씩 달라질수 있다.
본 예시에서는 번호가 낮은 인접 노드부터 (주로 많이 쓰이는 기준)
- [Step 1] 시작 노드인 '1'을 스택에 삽입하고 방문처리합니다.
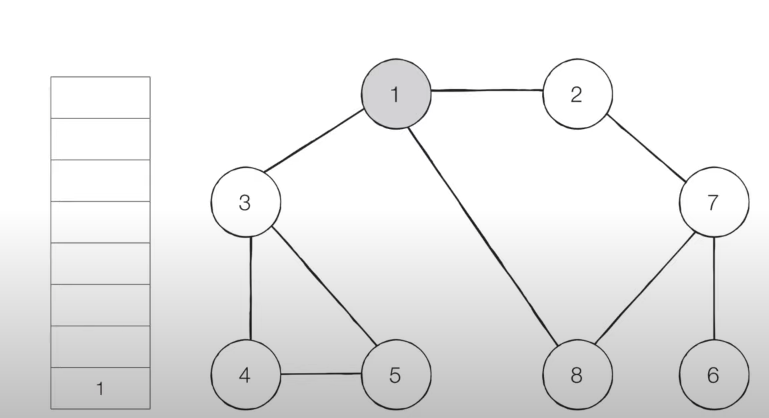
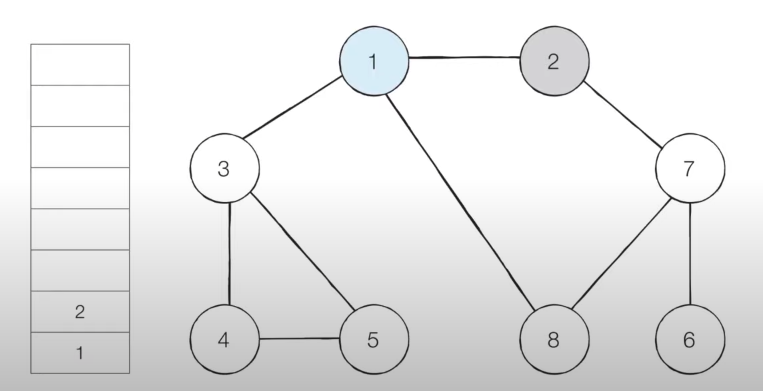
- [Step 2] 스택의 최상단 노드인 '1'에 방문하지 않은 인접 노드 '2', '3', '8'이 있습니다.
- 이 중에서 가장 작은 노드인 '2'를 스택에 넣고 방문 처리를 합니다.
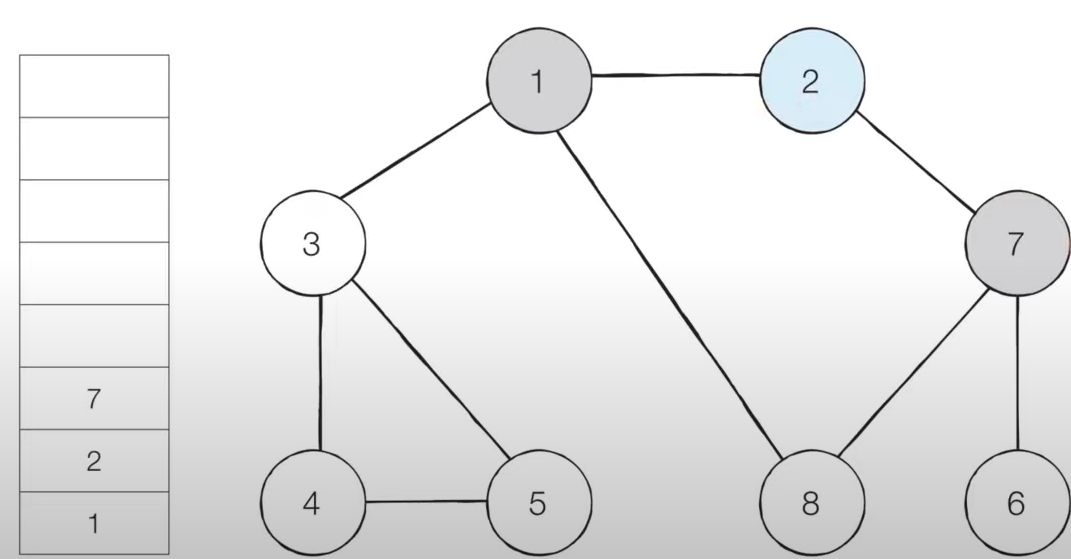
- [Step 3] 스택의 최상단 노드인 '2'에 방문하지 않은 인접 노드 '7'이 있습니다.
- 따라서 '7'번 노드를 스택에 넣고 방문 처리를 합니다.
- [Step 4] 스택의 최상단 노드인 '7'에 방문하지 않은 인접 노드 '6', '8'이 있습니다.
- 이 중에서 가장 작은 노드인 '6'을 스택에 넣고 방문 처리를 합니다.
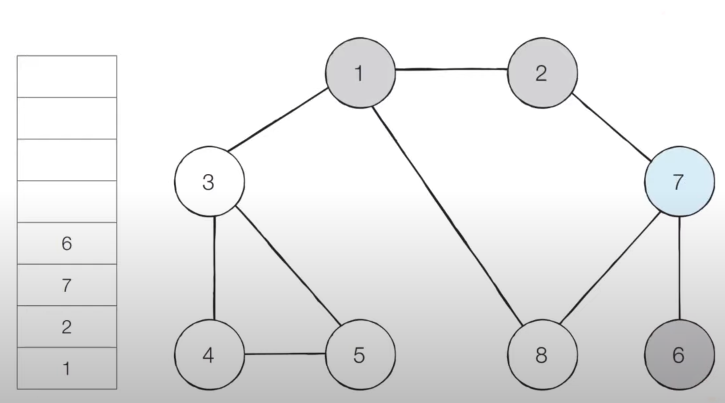
- [Step 5] 스택의 최상단 노드인 '6'에 방문하지 않은 인접 노드가 없습니다.
- 따라서 스택에서 '6'번 노드를 꺼냅니다.
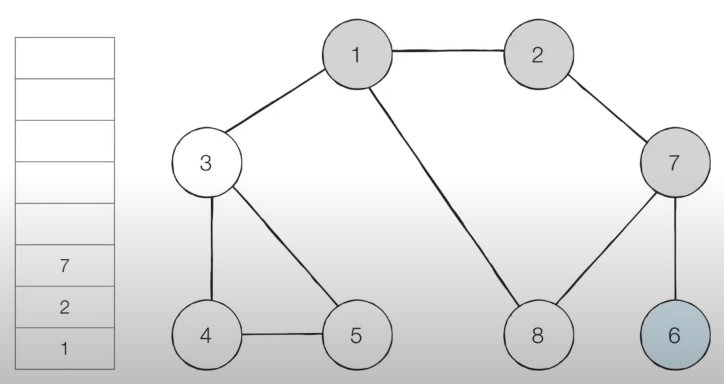
- [Step 6] 스택의 최상단 노드인 '7'에 방문하지 않은 인접 노드 '8'이 있습니다.
- 따라서 '8'번 노드를 스택에 넣고 방문 처리를 합니다.
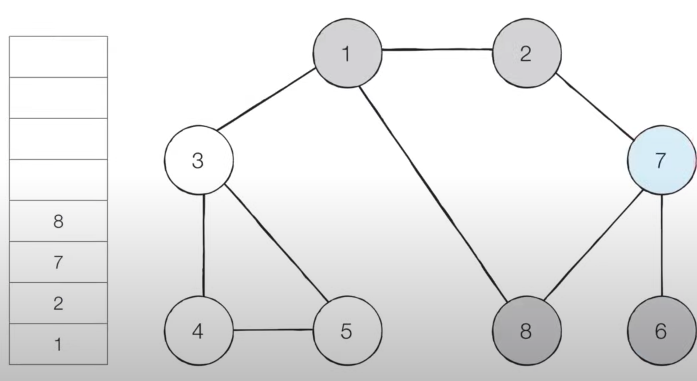
- 이러한 과정을 반복하였을 때 전체 노드의 탐색 순서(스택에 들어간 순서)는 다음과 같습니다.
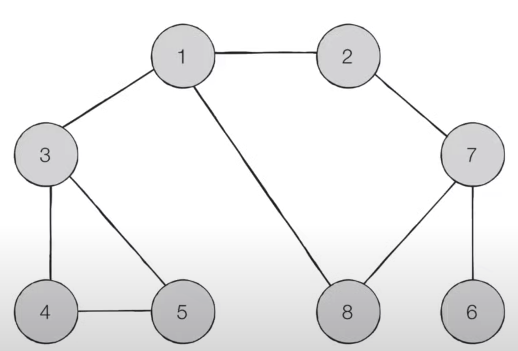
탐색순서 : 1 -> 2 -> 7-> 6-> 8-> 3-> 4-> 5
소스 코드
let graph = [
[], //0번노드는 주로 없는경우가 많아서 이렇게 비어있는 칸으로 두는경우가 많다.
[2, 3, 8], //1번 노드에 연결된 간선들
[1, 7], //2번 노드에 연결된 간선들
[1, 4, 5], //3번 노드에 연결된 간선들
[3, 5], //4번 노드에 연결된 간선들
[3, 4], //5번 노드에 연결된 간선들
[7], //6번 노드에 연결된 간선들
[2, 6, 8], //7번 노드에 연결된 간선들
[1, 7] //8번 노드에 연결된 간선들
]
let visited = Array(9).fill(false)
// 마찬가지로 0번 인덱스를 쓰지않으면
// 노드번호와 인덱스번호를 일치시킬수 있으므로 직관적으로 코딩이 가능하다.
function dfs(graph, v, visited) {
// 현재 노드를 방문 처리
visited[v] = true;
console.log(v)
// 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for(let index in graph[v]) {
if(!visited[graph[v][index]]) { // 이부분 코드 주의.. python이랑 달라서 고치는데 힘들었다.
//방문했다면 true 안했다면 false 인데 거기에 not
dfs(graph, graph[v][index], visited)
}
}
}
dfs(graph, 1, visited)
BFS
업데이트 예정
