Batch Normalization, Layer Normalization, RMSNorm의 비교

Effy_ee·2024년 9월 9일

NLP

6번째 주차

목록 보기

1/1

1. Batch Normalization

내부 공변량 변화를 줄이기 위해 사용

1.1 수식 정의

미니배치 평균과 분산 계산
주어진 미니배치에서 평균과 분산을 계산한다.
평균: $\mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i$
분산: $\sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2$ (여기서 $m$ 은 미니배치의 크기)
정규화: 계산된 평균과 분산을 사용하여 입력을 정규화한다. 정규화된 값은 다음과 같다.
$\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$
(여기서 $\epsilon$ 은 수치적 안정성을 위한 작은 상수)
스케일링 및 이동: 정규화된 값에 학습 가능한 파라미터인 스케일 파라미터 $\gamma$ 와 이동 파라미터 $\beta$ 를 적용한다.
$y_i = \gamma \hat{x}_i + \beta$

Batch Normalization 같은 경우, 각 시점(time step)마다 다른 데이터가 연속적으로 나오는 sequential 한 형태의 데이터의 경우 배치 정규화를 적용시키기 어렵다.
미니배치 내 데이터의 평균과 분산을 기반으로 정규화하는 Batch Normalization은 시계열 데이터에서 각 시점의 데이터의 분포를 상이하게 만들 수 있고 이는 일관되지 않은 학습 결과를 만들어 낼 수 있기 때문이다. 또한, 시간적 의존성을 무시하고 각 시점의 데이터를 독립적으로 처리하기에 sequential 데이터의 특성을 제대로 반영하지 못할 수 있다. 예를 들어, 주식처럼 시간의 흐름이 중요한 데이터의 경우에는 단순히 정규화를 진행하면 안된다. 그래서 등장한 것이 Layer Normalization이다.

Batch Normalization은 데이터의 특성(feature) 단위로 평균과 표준편차를 구한다면, Layer Normalization은 data sample 단위로 평균과 표준 편차를 구하는 것을 의미한다.
features : 데이터의 특성 (variables) / data sample : 데이터의 관측치

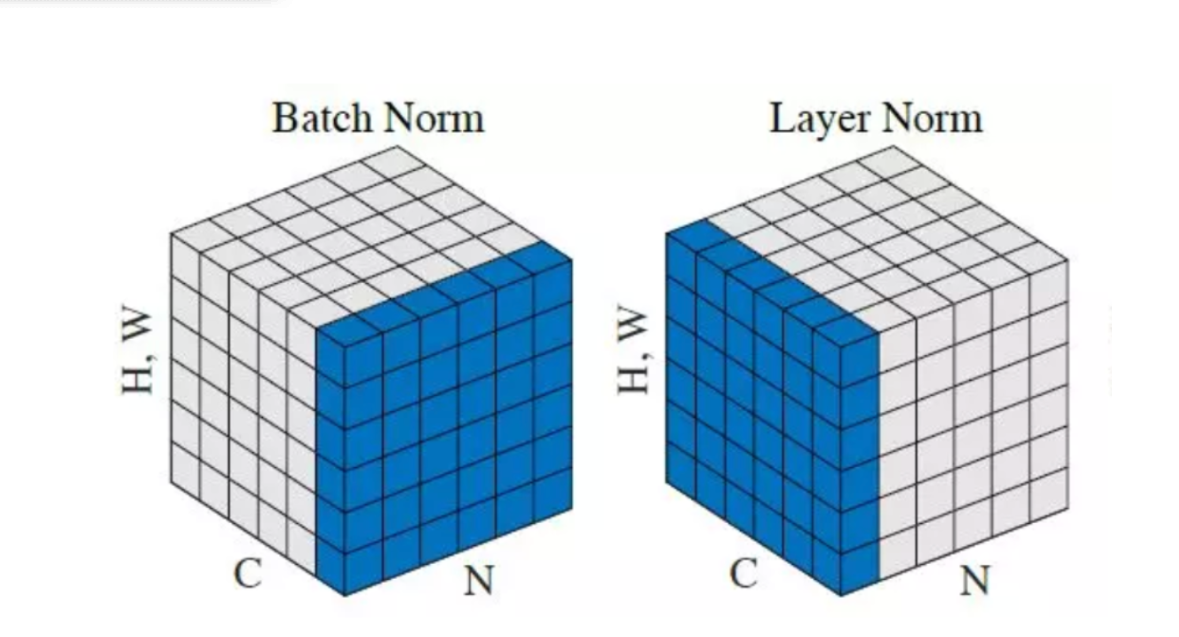
위 그림을 바탕으로 Batch Normalization과 Layer Normalization의 차이를 확인해보면
(N : 미니배치의 차원 / C : 채널 차원)

위 그림에서 보면, Batch Normalization은 서로 다른 관측치(C)에 대해서 특성(N)별 Normalization을 수행하는것이고
Layer Normalization은 서로 다른 특성(N)에 대해 같은 관측치(C)에 대해 Normalization을 수행하는 것이다.

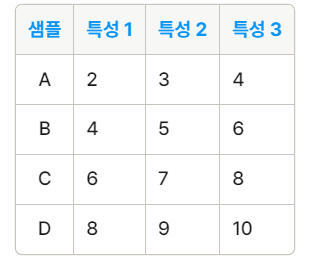
A. Batch Normalization

Batch Normalization은 각 특성별로 정규화를 수행

특성 1에 대한 정규화

평균: (2 + 4 + 6 + 8) / 4 = 5
분산: ((2-5)² + (4-5)² + (6-5)² + (8-5)²) / 4 = 5

A: (2 - 5) / √5 = -1.34
B: (4 - 5) / √5 = -0.45
C: (6 - 5) / √5 = 0.45
D: (8 - 5) / √5 = 1.34

특성 2와 3에 대해서도 동일하게 진행한다.

B. Layer Normalization

Layer Normalization은 각 샘플에 대해 모든 특성을 동시에 정규화

샘플 A에 대한 정규화

평균: (2 + 3 + 4) / 3 = 3
분산: ((2-3)² + (3-3)² + (4-3)²) / 3 = 0.67

A의 특성 1: (2 - 3) / √0.67 = -1.22
A의 특성 2: (3 - 3) / √0.67 = 0
A의 특성 3: (4 - 3) / √0.67 = 1.22

샘플 B, C, D에 대해서도 동일하게 진행한다.

2. Layer Normalization

신경망의 각 층에서 입력 데이터의 정규화를 수행한다.
내부 공변량 이동문제를 해결하기 위해 고안된 정규화 기법이다.

2.1 수식 정의

입력 벡터: $X = [x_1, x_2, ..., x_d]$
평균: $\mu = \frac{1}{d} \sum_{i=1}^{d} x_i$
분산: $\sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2$
정규화: $\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}$
(여기서 $\epsilon$ 은 분모가 0이 되는 것을 방지하기 위한 상수)
스케일링 및 이동: $y_i = \gamma \hat{x}_i + \beta$
$\gamma$ 와 $\beta$ 는 학습 가능한 파라미터
결과: $𝑦=[𝑦1,𝑦2,...,𝑦𝑑]$

각 배치마다 평균과 분산을 계산해야 하므로 계산 비용이 증가한다. RNN과 같은 순차적 모델에서는 각 타임 스텝에서 정규화를 적용해야 하므로 오버헤드가 발생할 수 있다.

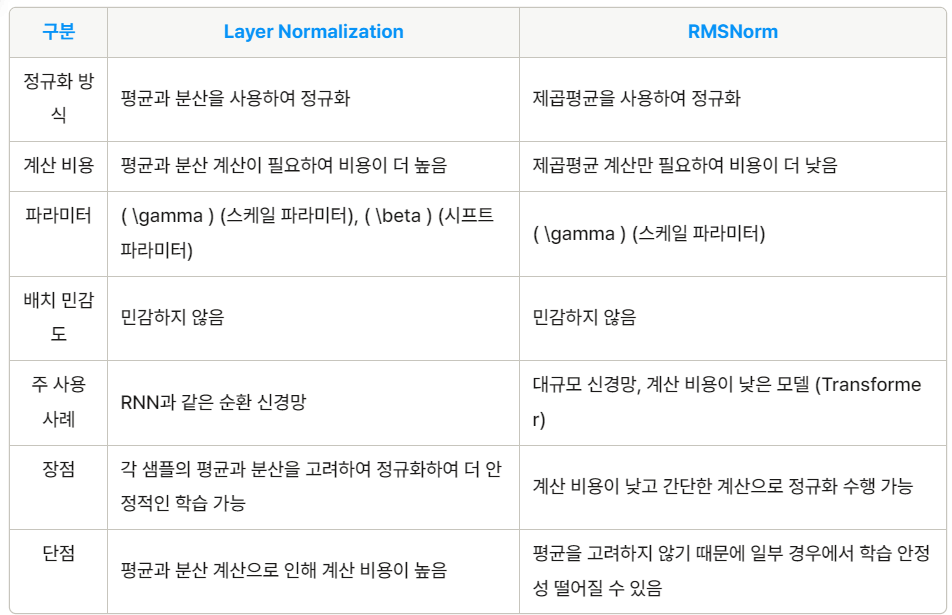
3. RMSNorm (Root Mean Square Normalization)

Layer Normalization과 유사하게 신경망의 입력을 정규화하는 방법
다만, RMSNorm은 각 입력의 평균과 분산을 고려하는 대신, 입력의 제곱평균을 사용하여 정규화를 수행

3.1 수식 정의

입력 벡터: $X = [x_1, x_2, ..., x_d]$
제곱 평균 계산
제곱 평균: $\text{RMS} = \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_i^2}$

분산 계산 (없음 LN과의 차이, 제곱평균이기에 가능)

정규화: $\hat{x}_i = \frac{x_i}{\text{RMS} + \epsilon}$
(여기서 $\epsilon$ 은 분모가 0이 되는 것을 방지하기 위한 작은 상수)
스케일링 및 이동 : $y_i = \gamma \hat{x}_i$
RMSNorm에서는 일반적으로 시프트 파라미터 $\beta$ 를 사용하지 않고, 스케일링 파라미터 $\gamma$ 만을 사용하여 정규화된 값에 대해 스케일링을 수행
출력: 𝑦=[𝑦1,𝑦2,...,𝑦𝑑]

4. 코드

A. LN (Layer Normalization)

import torch
import torch.nn as nn

# Define a LayerNorm layer
layer_norm = nn.LayerNorm(normalized_shape)

# Apply LayerNorm to the output of a layer
normalized_output = layer_norm(output)

B. RMSNorm

import torch
import torch.nn as nn

class RMSNorm(nn.Module):
    def __init__(self, normalized_shape, eps=1e-8):
        super(RMSNorm, self).__init__()
        self.eps = eps
        self.gamma = nn.Parameter(torch.ones(normalized_shape))

    def forward(self, x):
        rms = torch.sqrt(torch.mean(x**2, dim=-1, keepdim=True))
        x_norm = x / (rms + self.eps)
        return self.gamma * x_norm

# Define an RMSNorm layer
rms_norm = RMSNorm(normalized_shape)

# Apply RMSNorm to the output of a layer
normalized_output = rms_norm(output)

출처: https://github.com/bzhangGo/rmsnorm

Effy_ee