문제 해석
- 수열 A의 크기를 입력받아 A의 크기 만큼 요소를 입력받는다. 입력 받은 후 수열 A에서 가장 긴 증가하는 부분 수열을 구하면되는 문제이다.
예시
수열 A의 크기(6), 수열 A의 요소가 아래와 같이 주어졌을 때 6 10 20 10 30 20 50

- 가장 긴 증가하는 부분 수열을 구해보자.
- 가장 긴 부분 수열은 육안으로 보기에 A' = {10, 20, 30, 50}인 것을 알 수 있을 것이다.
- 그렇다면, 가장 긴 부분 수열을 구하려면 어떻게 해야할까?
- 가장 긴 부분 수열을 구하기 위해서는 생각해야할 조건이 있다.
조건
○ 이웃한 숫자간의 차이가 작아야한다. - 이웃한 숫자간의 차이가 작아야더 많은 숫자가 들어가니까 - 예를 들어보자 - 수열이 {10, 20, 30, 40, 50}과 {10, 15, 20, 25, 30, 35, 40, 45, 50}가 있다. - 각 수열은 10 ~ 50까지의 수열이지만 이웃한 숫자의 차이만 다르다 (10과 5로) -> 그렇기 때문에 차이가 적을수록 많이 들어간다. (물론 이 문제는 이미 주어진 숫자들을 가지고 가장 긴 증가하는 부분수열을 구하는 문제이지만 푸는데 필요한 조건이다.)
위의 조건이 필요한 이유의 예시
백준에서 주어진 예시로는 설명하기 어려움으로 새로 예시를 들어보겠다! 수열 A = {10, 20, 15, 10, 20, 40, 30, 40, 45, 50} 이 있다고 하자 가장 긴 부분 수열을 구하고자 했을 때 가장 긴 부분 수열은 {10, 15, 20, 30, 40, 45, 50}인 것을 확인할 수 있다. 하지만, 순서대로 '직전에 넣은 요소보다 큰가?'만 비교했다면 수열은 {10, 20, 40, 45, 50}이 만들어졌을 것이다.이러한 이유로 숫자간의 차이가 적어야 더 많은 수가 들어갈 수 있다.
Q. "엇? 그러면 직전 요소보다 작은 수를 발견하면 다시 처음으로 돌아가서 작은 수 부터 넣어야할까?"
A. "아니다. 이 문제는 가장 긴 증가하는 수열의 크기만을 구하면 된다. 마주친 작은 수와 가장 가까우면서 마주친 작은 수보다 크면 바꿔치기하면 된다."
-> 말이 조금 정리가 안돼서 난잡한느낌인데,,, 아래 그림을 보면 바로 이해할 수 있을 것이다.
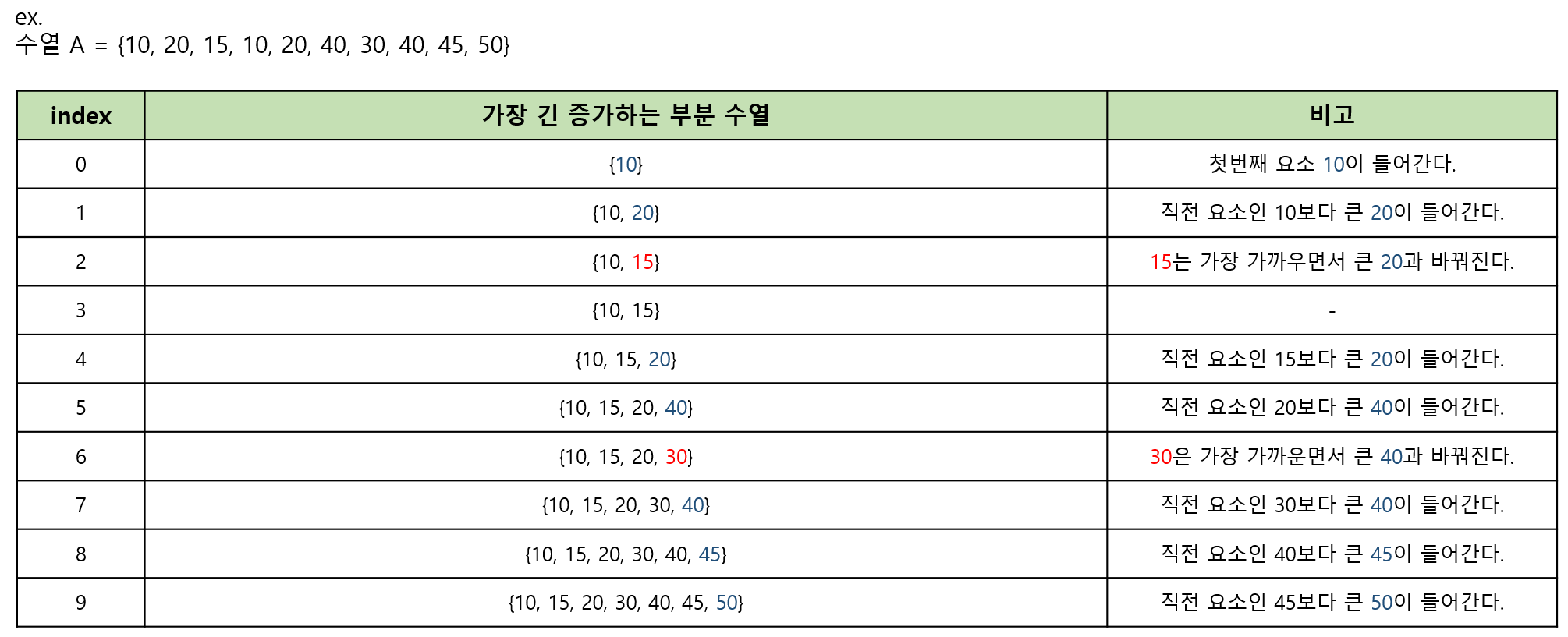
요소가 들어가거나 바꿔지는 로직은 아래와 같다
if (LISA[length - 1] < keyFromA) { //만약 직전에 들어간 요소가 다음 탐색 요소보다 작으면
length++;
LISA[length - 1] = keyFromA; //들어가기(추가)
}else{ //만약 직전에 들어간 요소가 다음 탐색 요소보다 작지 않으면
//이분탐색
int start = 0;
int end = length;
while(start < end){
int middle = (start+end)/2; //중간 값
if(LISA[middle] < keyFromA){ //중간값과 비교 대상의 key값을 비교했을 때 중간값이 작을 경우
//크기를 증가시킨다. (시작점을 증가)
start = middle+1;
}else{ //중간값과 비교대상의 key값을 비교했을 때 중간값이 더 클 경우
//크기를 감소시킨다. (끝점을 감소)
end = middle;
}
}
//가장 가까운 원소의 값을 넣어준다.
LISA[start] = keyFromA; // 바꾸기
}코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[] A; //수열A 요소 배열
static int[] LISA; //가장 긴 수열 A의 부분 수열
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine()); //수열 A의 크기
A = new int[N]; //수열A 요소 배열 초기화(원본)
LISA = new int[N]; //가장 긴 부분 수열 초기화(결과 구할때 사용하는 배열)
st = new StringTokenizer(br.readLine());
for(int i = 0; i < N; i++){ //수열A의 요소 입력받기
A[i] = Integer.parseInt(st.nextToken());
}
// LISA (가장 긴 부분수열) 초기 값으로 첫 번째 수열의 값을 가진다.
LISA[0] = A[0];
int length = 1; //가장 긴 부분 수열의 길이 저장하는 변수
for(int i = 1; i < N; i++){ //첫번째 수열값이 시작점이니 1부터 시작
int keyFromA = A[i];
// 만약 key가 LIS의 마지막 값보다 클 경우 추가해준다.
if (LISA[length - 1] < keyFromA) {
length++;
LISA[length - 1] = keyFromA;
}else{ //만약 이미 들어간 배열에서 작지 않으면
//배열을 처음부터 끝까지 돌면서 가까운 값을 고르면 오래 걸리기 때문에 이분탐색을 해준다.
int start = 0;
int end = length;
while(start < end){
int middle = (start+end)/2; //중간 값
if(LISA[middle] < keyFromA){ //중간값과 비교 대상의 key값을 비교했을 때 중간값이 작을 경우
//크기를 증가시킨다. (시작점을 증가)
start = middle+1;
}else{ //중간값과 비교대상의 key값을 비교했을 때 중간값이 더 클 경우
//크기를 감소시킨다. (끝점을 감소)
end = middle;
}
}
//가장 가까운 원소의 값을 넣어준다.
LISA[start] = keyFromA;
}
}
System.out.println(length);
}
}결과

느낀 점
전에 관련된 비슷한 문제를 푼 적이 있다. 11053_가장 긴 증가하는 부분 수열문제였는데 그때는 시작점을 바꿔가며 길이를 전부 구한 후 최대 길이를 뽑아냈어서 약간 다르다... 무엇보다 지금 이분탐색을 풀고 있다보니 전에 풀었던 문제보다 이 문제가 더 익숙한 느낌,,,
이 문제로 단계별 풀어보기 ; 이분탐색은 끝이 났다 다음 포스트부턴 우선순위 큐 문제인데 열심히 정리해보겠다!
