백준 1010 다리 놓기 [JAVA]

Ga0·2023년 6월 2일

baekjoon

목록 보기

63/137

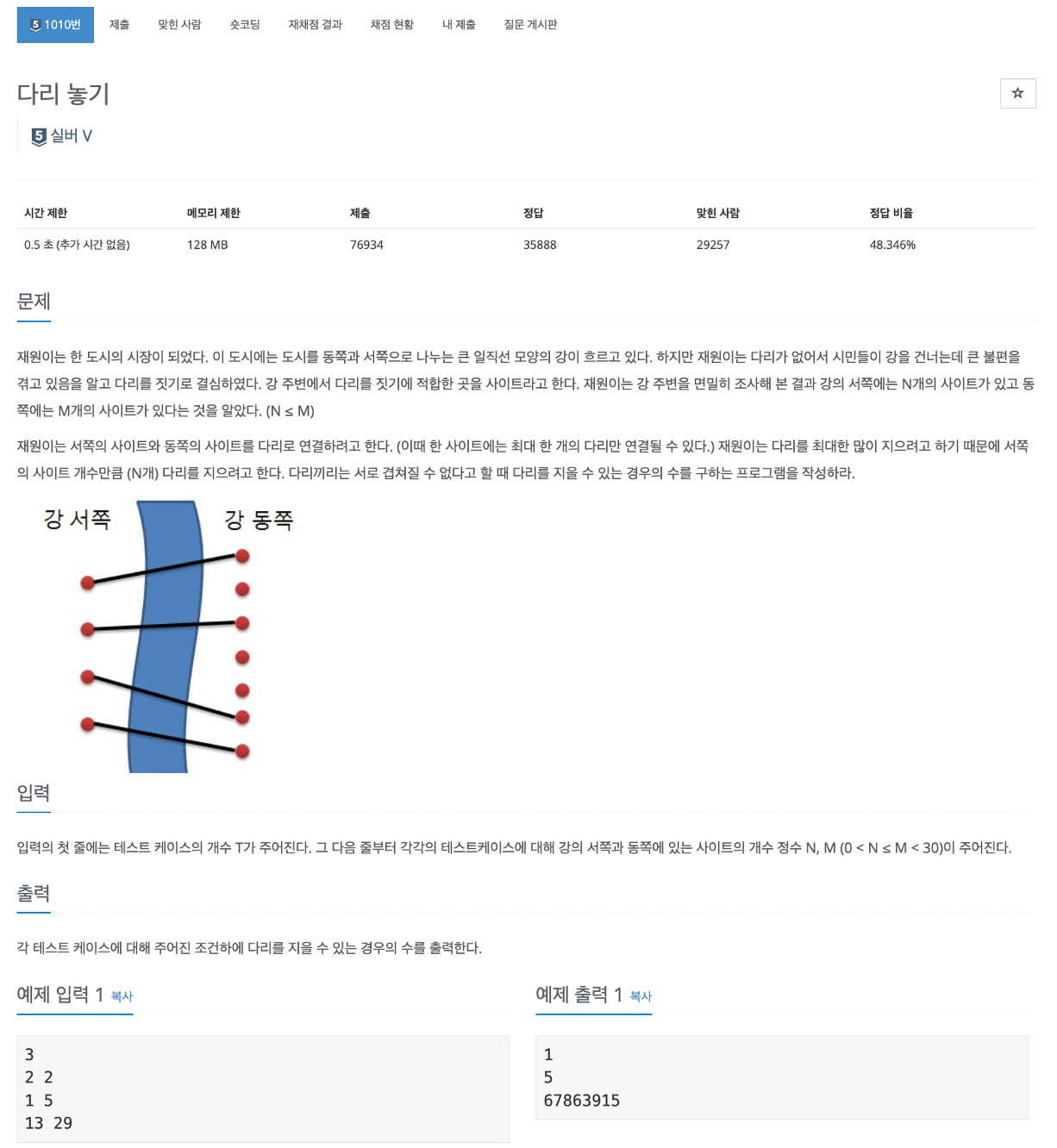
문제 해석

일단, 테스트 케이스의 개수(T)를 입력받고, 테스트 케이스의 개수만큼 N, M의 조합을 입력받는다.
N은 서쪽의 사이트 개수이고, M은 동쪽의 사이트 개수이다.
서쪽과 동쪽일 잇는 다리를 만들려고 하는데 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수(N)만큼 다리를 짓는 대신, 지을 수 있는 다리끼리는 서로 겹쳐질 수 없다.


즉, 서로 다른 n개에서 순서를 생각하지 않고 r개를 뽑는 것을 n개에서 r개를 택하는 것을 의미한다.
=> 왜냐면, 다리가 겹치면 안된다는 것은 CROSS도 안된다는 뜻이다.
=> 그말은 즉슨, 순서를 고려하지 않으면 경우의 수만 따지기 때문에 겹치지 않는, 유효한 경우의 수로 생각하면 된다.
조합의 공식은 mCn = m! / n!(m-n)! 이다.

 n  m
10 12인 경우, 12! / 10! x (12-10)! = 12! / 10! x 2! = 12x11/2x1 = 66

-> 이 과정을 이해했다면 하나의 식으로 정리할 수 있다.
->  m부터 m−n까지 곱을 n!만큼 나누면 된다.

틀린 코드

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int T = Integer.parseInt(br.readLine()); //테스트 개수


        for(int i = 0; i < T; i++){
            StringTokenizer st = new StringTokenizer(br.readLine());

            int N = Integer.parseInt(st.nextToken());
            int M = Integer.parseInt(st.nextToken());

            bw.write(getBridge(M, N) + "\n");
        }
        
        br.close();

        bw.flush();
        bw.close();
    }

    static long getBridge(int M, int N)
    {
        long result = 1; //0과 1 팩토리얼은 1이기 때문에 1부터 시작

        //mCn
        for (int i = (M - N) + 1; i <= M; i++) {
            result *= i;
        }

        for (int i = 1; i <= N; i++) {
            result /= i;
        }
        return result;
    }
}

틀린 결과

틀린 이유

왜 틀렸는지 찾아보니까 이런식으로 하게 되면 overflow문제가 발생한다.
쉽게 말하자면 현재 조건이 N, M (0 < N ≤ M < 30)인데, 만약 N = 25일때를 생각해보면 20!만으로도 64비트 정수형의 범위를 넘어가게 되는데, 25!은 말할 것도 없다 정수형으로 표현할 수 없는 overflow가 발생한다.
다시 말해 다른 방법을 구해야하는데, 나는 방법이 떠오르질 않아서 1010 : 다리놓기-참고-포스트을 참고해 문제를 풀 수 있었다.
아래의 성질을 이용하는 건데,
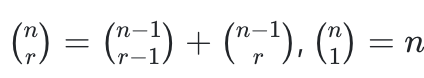
nC1 = n인 것은 딱히 증명을 하지않아도 분모가 1이니 n이 나올 수밖에 없다.
nCr = n-1Cr-1 + n-1Cr인 것을 증명하는 것은 아래와 같이 작성했다.

맞은 코드

import java.util.*;
import java.io.*;

public class Main {
    private final static int MAX = 30; //N과 M이 30까지만 입력받기 때문에
    static int[][] dp = new int[MAX + 1][MAX + 1]; //조합을 계산할 때 사용하는 배열

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int T = Integer.parseInt(br.readLine()); //테스트 개수

        createCombie(); //조합 구하는 배열 만들기

        //테스트 개수만큼  다리를 지을 수 있는 경우의 수 구하기
        for (int i = 0; i < T; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());

            int r = Integer.parseInt(st.nextToken());
            int n = Integer.parseInt(st.nextToken());

            bw.write(dp[n][r] + "\n");
        }

        br.close();
        bw.flush();
        bw.close();
    }

    static void createCombie(){ //조합 배열 만드는 메소드
        //nC1 = n인 속성을 이용
        for (int i = 1; i <= MAX; i++) {
            dp[i][1] = i;
        }

        //nCr = n-1Cr-1 + n-1Cr의 속성을 이용
        for (int j = 2; j <= MAX; j++) {
            for (int k = 2; k <= MAX; k++) {
                dp[j][k] = dp[j - 1][k - 1] + dp[j - 1][k];
            }
        }
    }
}